Université Rennes 1, Année L1, 2017-2018
Mathématiques 1
page mise à jour le 13/12/2017 à 10:30
Infos générales
Module MAT1, Mathématiques 1 à l'ISTIC, Enseignant : Matthieu Romagny
Page web du cours MAT1 :
ici.
Pour connaître les horaires exacts des
créneaux de cours semaine par semaine, ainsi que les salles, regardez
l'emploi du temps en ligne.
Documents
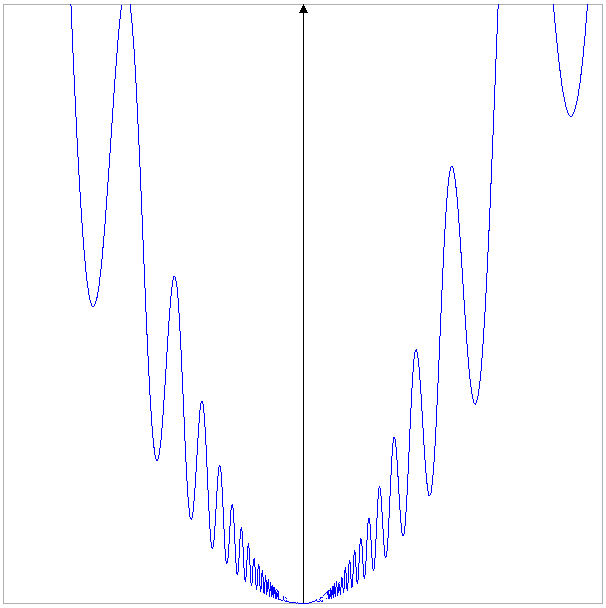
Exemple d'une fonction qui admet un minimum local en 0, mais qui
même
quand on se place sur un tout petit intervalle I autour de 0 n'est ni
croissante ni décroissante sur I. Prenons la fonction définie par
f(x)=x²(sin(1/x)+2). Comme -1≤sin(1/x)≤1, on a
1≤sin(1/x)≤3 donc en multipliant par x² on obtient
x²≤f(x)≤3x². D'après le théorème des gendarmes, la fonction f
tend vers 0 lorsque x tend vers 0, et de plus le graphe de f est tout
entier situé entre les deux paraboles d'équations y=x² et y=3x².
Voici le graphe de cette fonction:
Les examens terminaux du module ANA :
2016-2017,
2015-2016,
2014-2015.
Attention : le module ANA était semblable au module MAT1, sauf
que le programme contenait des équations différentielles, et
ne contenait pas de probabilités.
Feuille 6
et solutions.
Feuille 5
et solutions.
Feuille 3
et solutions.
Feuille 2
et solutions.
Feuille 1
et solutions. Correction plus détaillée de
l'exercice 1.15.
Contrôle no 2 et
corrigé.
Contrôle no 1 et
corrigé.
Résumé séance par séance
Mardi 12 décembre
Exercices : Examen terminal 2016-2017.
Enoncé : voir ci-dessus. Réponses :
ici.
Lundi 11 décembre
Cours : probabilités : notions d'univers, d'événement, de variable
aléatoire. Loi d'une variable aléatoire. Exemples de la loi de Bernoulli
de paramètre p (0<p<1) et de la loi de Bernoulli de paramètres n et p
(n∈ℕ et 0<p<1).
Exercices faits : 6.9, 6.12, 6.13.
Jeudi 7 décembre
Cours : aucun.
Exercices faits : 6.3.
Pour lundi 11 décembre :
- relire le cours.
Mercredi 6 décembre
Cours : aucun (retour sur ex 6.1 et les
interprétations combinatoires).
Exercices faits : 6.3.
Pour jeudi 7 décembre :
- relire le cours.
Mardi 5 décembre
Cours : dénombrements: cardinal et bijections,
retour sur les parties de cardinal k fixé d'un ensemble
fini à n éléments, notion de "interprétation combinatoire",
dénombrement des tirates (avec ou sans ordre; avec ou sans
répétition).
Exercices faits : 6.1 et 6.2.
Pour mercredi 6 décembre :
- relire le cours.
Lundi 4 décembre
Cours : début du chapitre probabilités: combinatoire,
dénombrement des permutations d'un ensemble fini,
parties d'un ensemble fini, coefficients binomiaux,
formule du triangle de Pascal.
Exercices faits : début du 6.1.
Pour mardi 5 décembre :
- relire le cours.
- faire l'exercice 6.2.
Jeudi 30 novembre
Cours : intégration des fractions rationnelles.
Exercices faits : 5.10, 5.11.
Pour lundi 4 décembre :
- relire le cours.
- terminer les exercices 5.9 et 5.11.
Mercredi 29 novembre
Cours : aucun.
Exercices faits : 5.7, 5.8.
Pour jeudi 30 novembre :
- relire le cours.
- regarder l'exercice 5.9.
Mardi 28 novembre
Cours : théorème de changement de variables pour les intégrales.
Exercices faits : 5.5, 5.6.
Pour mercredi 29 novembre :
- relire le cours.
Lundi 27 novembre
Cours : intégrales impropres ou généralisées,
intégration par parties, exemples.
Exercices faits : début exercice 5.5.
Pour mardi 28 novembre :
- relire le cours.
- terminer exercice 5.5.
Jeudi 23 novembre
Cours : retour sur la question de la dérivabilité d'une fonction en un
point ; exemple de la fonction f(x)=exp(1/x²) en x=0.
Intégrales : définition en termes d'aire, exemples,
linéarité (intégrale d'une somme de deux fonctions ou du multiple
d'une fonction par une constante), positivité, relation de Chasles.
Exercices faits : 5.1, 5.2-a-b-c-d.
Pour lundi 27 novembre :
- relire le cours.
- terminer exercice 5.2. Terminer l'exercice 3.18 (c)
avec une attention particulière pour les propriétés de la fonction
au voisinage des points d'abscisse -1 et 1 (continuité, dérivabilité).
Mercredi 22 novembre
Cours : début du cours sur l'intégration : primitives, exemples.
Exercices faits : 3.18 (c) commencé.
Pour jeudi 23 novembre :
- relire le cours.
Mardi 21 novembre
Cours : aucun.
Exercices faits : 3.15, 3.19.
Pour mercredi 22 novembre :
- relire le cours ! même si nous n'avons pas fait
de nouveau cours aujourd'hui.
- travailler l'exercice 3.18 pour vous entraîner
aux études de fonctions complètes.
Lundi 20 novembre
Cours : utilisation de la dérivée seconde pour déterminer
si un point critique est extremum local, asymptotes.
Plan d'étude d'une fonction.
Exercices faits : 3.10.
Pour mardi 21 novembre :
- relire le cours.
- préparer exercice 3.15.
Jeudi 16 novembre
Cours : dérivées d'ordre supérieur, fonctions convexes et concaves,
points d'inflexion.
Exercices faits : 3.9.
Pour lundi 20 novembre :
- relire le cours.
Mardi 14 novembre
Cours : théorème des valeurs intermédiaires (TVI),
fonctions croissantes et décroissantes, théorème des
accroissements finis (AF), l'image d'un segment par une application
continue est un segment.
Exercices faits : 3.7 (a) et (e), début du 3.9.
Pour jeudi 16 novembre :
- relire le cours.
- terminer exercice 3.9 et faire le 3.10.
Lundi 13 novembre
Cours : théorème "règle de l'Hôpital" (sa connaissance n'est pas
obligatoire), étude globale des fonctions : définition des minima,
maxima et points critiques.
Exercices faits : 3.4 et 3.6.
Pour mardi 14 novembre :
- relire le cours.
Jeudi 9 novembre
Cours : dérivées, suite et fin : dérivées de sommes, produits, quotients, composées.
Tous les exemples de fonctions classiques (puissances, fonctions trigonométriques,
fonctions trigonométriques réciproques, exponentielle et logarithme).
Exercices faits : 3.5.
Pour lundi 13 novembre :
- relire le cours.
- faire les exercices 3.4 et 3.6 (des étudiant-e-s passeront au tableau).
Mardi 7 novembre
Cours : dérivée d'une fonction.
Exercices faits : 3.2, et 3.3 a-b-c-d-e.
Pour jeudi 9 novembre :
- relire le cours.
- terminer l'exercice 3.3. Celle ou celui qui sait donner une
réponse justifiée pour (i) gagne un carambar.
Lundi 6 novembre
Cours : continuité ; calculs de limites : théorème des gendarmes ;
théorèmes de comparaison entre exponentielles, polynômes et logarithmes ;
fractions rationnelles ; limite de sin(x)/x lorsque x→1.
Exercices faits : 3.1.
Pour mardi 7 novembre :
- relire le cours.
- travailler les exercices 3.2 et 3.3.
Jeudi 26 octobre
Cours : Limites de fonctions de variable réelle : limites en x0,
en x0+, en x0-, en +∞,
en -∞.
Exercices faits : 2.13, 2.14.
Pour lundi 6 novembre :
- relire le cours.
- réviser la fonction arctan !
- faire l'exercice 3.1.
Mardi 24 octobre
Cours : Fractions rationnelles ; décomposition en éléments simples.
Exercices faits : 2.18, 2.8, 2.15.
Pour jeudi 26 octobre :
- relire le cours.
- faire l'exercice 2.14.
Lundi 23 octobre
Cours : Fonctions réciproques classiques : arccos, arcsin, arctan, logarithme.
Exponentielles et logarithmes en base a.
Exercices faits : 2.7, 2.11.
Pour mardi 24 octobre :
- relire le cours.
- tracer le graphe de la fonction f:ℝ ⟶ ℝ, f(x)=arccos(cos x).
En déduire la réponse aux questions a-b-c de l'exercice 2.18.
Vendredi 20 octobre
Cours : Fonctions polynômes : définition, degré,
division euclidienne.
Exercices faits : 2.9.
Pour lundi 23 octobre :
- relire le cours.
- préparer les exercices 2.7 et 2.11.
Jeudi 19 octobre
Cours : Fonctions périodiques, fonctions bijectives,
bijections réciproques.
Exercices faits : 2.2, 2.3 (questions a-b-c-d), 2.6.
Pour vendredi 20 octobre :
- relire le cours. Faire l'exercice 2.5.
Lundi 16 octobre
Cours : Fonctions numériques d'une variable réelle f:A⟶ℝ,
image d'un point de la source (ou ensemble de départ),
antécédents d'un point du but (ou ensemble d'arrivée).
Image d'une fonction, restriction, prolongement.
Opérations sur les fonctions : composition, addition, multiplication.
Graphe, fonctions paires et impaires.
Exercices faits : 2.1.
Pour jeudi 19 octobre :
- relire le cours en vérifiant votre compréhension sur
les exercices 2.2 et 2.3.
Jeudi 12 octobre
Cours : Racines carrées d'un nombre complexe, équation du second
degré à coefficients complexes.
Exercices faits : 1.5, 1.8, 1.10, 1.11.
Pour lundi 16 octobre :
- relire le cours.
- Exercices à rédiger sur feuille (que je ramasserai) : 1.14(d) et 1.15(a).
Note importante : dans 1.14(d) l'équation à résoudre est bien
z²+(2+i)z−1+7i=0 (dans la feuille de TD le =0 est oublié !).
- Exercices à rédiger pour vous : 1.14(b), fin de l'exercice 1.15.
- Vous pouvez regarder également les exercices 1.16 et 1.17.
Mercredi 11 octobre
Cours : Racines carrées d'un nombre complexe, équation du second
degré à coefficients complexes.
Exercices faits : 1.5, 1.8, 1.10, 1.11.
Solutions de 1.11 : sin³x= (−¼)·(sin(3x)−3 sin(x)) et
cos²(3x)sin(5x)=¼·(sin(11x) + 2 sin(5x) − sin(x)).
Pour la prochaine fois :
- relire le cours.
- Regarder les exercices 1.12, 1.13, 1.14.
Mardi 10 octobre
Cours : Propriétés de la conjugaison.
Fonction exponentielle complexe.
Passage de la forme algébrique à la forme trigonométrique
(ou à la forme exponentielle) et réciproquement.
Linéarisation.
Exercices faits : 1.2.
Pour la prochaine fois :
- relire le cours.
- Faire l'exercice 1.5.
Lundi 9 octobre
Cours : nombres complexes, addition, multiplication. Conjugué, division.
Interprétation géométrique dans le plan.
Module et argument.
Ecritures algébrique, trigonométrique et exponentielle.
Exercices faits : 1.1.
Pour la prochaine fois :
- relire le cours.
- Lire et comprendre la feuille accessible
ici.
Déroulement prévu pour le cours (octobre à décembre 2017)
Voici un tableau prévisionnel du déroulement du cours. Ce tableau
est donné à titre purement indicatif : il pourra y avoir de petites modifications.
Semaine
|
Dates
|
nombre d'heures de cours
|
contrôles
|
Contenu
|
Semaine 1
|
9 au 13 oct
|
8h
|
|
nombres complexes
|
Semaine 2
|
16 au 20 oct
|
6h
|
|
fonctions classiques réelles
|
Semaine 3
|
23 au 27 oct
|
6h |
contrôle 1
|
fonctions classiques réelles ; étude locale
d'une fonction réelle
|
Vacances
|
30
oct au 3 nov
|
X
|
|
|
| Semaine 4 |
6 au 10 nov
|
6h |
|
étude locale d'une fonction réelle |
| Semaine 5 |
13 au 17 nov
|
6h |
|
étude globale d'une fonction réelle
|
| Semaine 6 |
20 au 24 nov
|
8h |
contrôle 2
|
étude globale d'une fonction réelle ;
intégration
|
| Semaine 7 |
27 nov au 1er déc
|
8h |
|
intégration
|
| Semaine 8 |
4 au 8 déc
|
8h |
|
probas
|
| Semaine 9 |
11 et 12 déc
|
4h
|
|
probas
|

