Le théorème central limite

Dans son discours de la méthode, Descartes affirmait la nécessité de « séparer chaque ensemble trop vaste pour pouvoir être pris en son entier en de plus petits que l'on sache manier ». L'étude des probabilités nous conduit à accomplir le chemin inverse ! En effet, chaque épreuve aléatoire prise individuellement n'amène que des enseignements limités, tandis que plus on en considère un grand nombre, plus s'en dégage une structure profonde.

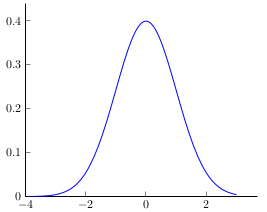
Le théorème central limite (appelé aussi théorème de Moivre-Laplace) formalise l'idée que la moyenne d'une suite d'épreuves aléatoires indépendantes de même loi s'approche, plus le nombre d'épreuves augmente, d'une loi normale - avec sa célèbre courbe de Gauss en forme de cloche.

L'énoncé est le suivant :

Considérons une suite (X_n) de variables aléatoires indépendantes, suivant une même loi de moyenne m=0 (pour simplifier) et d'écart type $σ$ . Notons S_n la moyenne des n premières variables X₁,...,X_n. Alors, $\sqrt{n} S_{n}$ converge en loi vers N(0, $σ$ ), la loi normale de moyenne m=0 et d'écart type $σ$ .

Lorsque les variables sont de moyenne m quelconque, le résultat devient :

$\frac{S_{n} - m}{\frac{σ}{\sqrt{n}}}$ converge en loi vers N(0,1) la loi normale centrée réduite.

En conséquence la limite de la probabilité

$P (a < \frac{S_{n} - m}{\frac{σ}{\sqrt{n}}} < b)$

vaut, lorsque n tend vers l'infini, l'intégrale

$\int_{a}^{b} \frac{e^{- \frac{x^{2}}{2}}}{\sqrt{2 π}} ⅆ x$

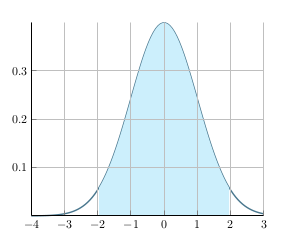
qui s'interprète comme la proportion d'aire sous la courbe précédente délimitée par les droites verticales x=a et x=b.

Lorsque a=-1.96 et b=1.96 cette proportion vaut environ 95%. Ainsi, l'aire hachurée vaut au moins 95% de l'aire totale sous la courbe de Gauss.

Ces considératons sont particulièrement utile en statistique pour étudier un caractère présent dans une population. Prenons l'exemple du caractère "avoir les yeux bleus".

Supposons qu'on sait le caractère présent dans la population avec une fréquence 30%. Alors, on peut estimer la proportion de personnes aux bleus dans un échantillon de n personnes prises au hasard. On obtient un intervalle de fluctuation.

Inversement, supposons qu'on ne connait pas la fréquence du caractère. Alors, la proportion de personnes aux bleus d'un échantillon de n personnes prises au hasard donne une valeur approchée de la fréquence du caractère dans la population.

Les résultats sont d'autant plus fiables que la taille de l'échantillon n est grand.

On peut se reporter aux énoncés et aux applications présents dans le document d'accompagement du programme officiel de mathématique du secondaire : Ressource officielle éduscol.

Pourquoi faire appel au théorème central limite dans le cas de la répétition d'épreuves de Bernouilli ? Rappelons qu'une épreuve de Bernouilli a seulement deux issues possibles : le succès avec probabilité p et l'échec avec une probabilité 1-p. Le jeu de pile ou face est un prototype d'épreuve de Bernouilli avec p=0.5.

On peut établir que la somme de n épreuves de Bernouilli indépendantes de même paramètre p suit une loi de Bernouilli B(n,p) de paramètres n et p. On peut donc explicitement exprimer la probabilité

$P (a < \frac{S_{n} - m}{\frac{σ}{\sqrt{n}}} < b)$

mais la formule donne une somme de coefficients binomiaux qui deviennent vite très lourds à manipuler. C'est pourquoi, une solution consiste à exploiter le théorèrme central limite qui en donne une valeur approchée (suffisamment précise plus n est grand, typiquement n>30, et que np et n(1-p) ne sont pas trop petits, typiquement >5).

Alors, on pourra considérer, avec un seuil de confiance à 95% que l'intervalle de fluctuation qui donne la variation de la proportion de succès pour n épreuves de Bernouilli sera

$[p - 1.96 \frac{\sqrt{p (1 - p)}}{\sqrt{n}}, p + 1.96 \frac{\sqrt{p (1 - p)}}{\sqrt{n}}]$

En classe seconde, on donne un intervalle de fluctuation moins précis (c'est-à-dire plus large), mais dont l'expression est plus simple :

$[p - \frac{1}{\sqrt{n}}, p + \frac{1}{\sqrt{n}}]$

Le théorème central limite au secours du commissaire Gévaudan.

P235.

Où on considère les mains comportant au moins un As. La probabilité d'une telle main est de 14.93%. Dès lors, la fréquence du caractère de la population étudiée est de p=0.1493.

Avec n=972 parties jouées, cela donne un intervalle de fluctuation au seuil de 95% de [0.126,0.172] (ou {0.117,0.182] si on considère le calcul simplifié). Gévaudan avec ses 18.62% de mains avec un As se trouve bien en dehors.

P7 et P243. Gévaudan estime que la probbailité de se faire toucher par une balle à 20% (p=0.2) en sortant de sa cachette. Il y a n=225 tirs par minutes (qui correspond à environ 75 tirs pour 3 truands, compatible avec un mode semi-automatique). Un intervalle de fluctuation au seuil de 95% est alors

[33.24,56.76] à multiplier par 225 pour obtenir le nombres d'impacts, à savoir en arrondissant [34,57]. Autrement dit, il peut estimer avec une confiance de 95%, recevoir entre 34 et 57 impacts de balle.

De même, lorsqu'il estime offrir 5% de risque de se faire toucher, il obtient, avec un seuil de confiance à 95%, un nombre d'impacts de balles de {4,17] (en arrondisant [4.84,17.66])

Quand la probabilité de se faire toucher tombe à 0.1%, attention, l'approximation par la loi normale tombe à l'eau (nous avons np =0.225<5).

Mais, dans ce cas, le calcul de la somme binomiale est aisée car comporte peu de termes. En effet, la probabilité de se prendre 0 ou 1 balle est de P₀+P₁= 97.83% où P_k est donnée par

$P_{k} = (\binom{225}{k}) {(0.001)}^{k} {(1 - 0.001)}^{225 - k}$

Une petite question pour terminer. Les conditions d'utilisation sont-elles satisfaites ? L'hypothèse d'indépendance est cruciale ; est-elle justifiée ?

Un telle hypothèse d’indépendance ne serait certainement pas valide dans le cas d'un tir automatique. En effet, la cadence élevée des rafales impose que des balles successives atteignent des zones plus ou moins voisines, en tout cas qui dépendent clairement l’une de l’autre. De même, un tireur d’élite ne remplirait pas du tout les conditions d’un tir aléatoire.

Par contre, je veux imaginer que c'est le cas pour des pistolets mitrailleurs en mode semi-automatique et manipulées par des narcos shootés jusqu’aux yeux.