L'aiguille de Buffon

En alternative au jeu de Pile ou Face, le naturaliste Georges-Louis Leclerc, comte de Buffon, présente en 1778 le jeu de l'aiguille dans son Essai d’Arithmétique morale,

"Je  suppose  que  dans  une  chambre,  dont  le  parquet  est  simplement  divisé  par  des  joints parallèles, on jette en l’air une baguette, & que l’un des joueurs parie que la baguette ne croisera aucune  des  parallèles  du  parquet,  &  que  l’autre  au  contraire  parie  que  la  baguette  croisera quelques-unes  de  ces  parallèles;  on  demande  le  sort  de  ces  deux  joueurs. On  peut  jouer  ce  jeu sur un damier avec une aiguille à coudre ou une épingle sans tête."

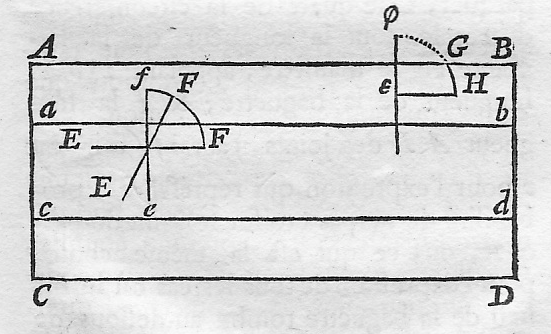
Le principe est le suivant :

On lance une aiguille de longueur a au-dessus d'un parquet dont les lames rectangulaires de de largeur b sont régulièrement disposées. On suppose que a<b.

On considère que le lancer se fait au hasard et que les positions de l'aiguille en retombant au sol sont équiprobables.

On cherche alors à estimer la probabilité p que l'aiguille tombe à cheval sur deux lames de parquet (qu'elle "coupe" une lame).

Explicitons la démonstration élégante d'Emile Borel.
Le nombre d'aiguilles qui coupent une lame de parquet est proportionnel à la longueur des aiguilles et inversement proportionnel à la distance entre les lattes. Donc p s'écrit sous la forme p= ka/b, avec k une constante à déterminer.
Pour déterminer la constante k, imaginons une aiguille en forme d'anneau de diamètre b.
Sa longueur - la circonférence d'un cercle - vaut π b. Peu importe comment l'aiguille tombe, son diamètre valant l'écart entre deux lames consécutives, elle coupe toujours par deux fois les lames.
D'où k a/b= 2, et avec a = πb dans ce cas particulier, nous obtenons k = 2/π.
Finalement, la probabilité qu'une aiguille coupe une lame est donc de 2a/πb.

En exploitant ce résultant, il est possible d'obtenir une approximation de π !

On lance un grand nombre d'aiguilles - on considère que les lancers d'aiguilles sont indépendants - on compte celles qui coupent une lame, nombre noté N. Alors, on peut estimer que pour un n grand, la proportion N/n sera proche de 2a/πb, et on en déduit que 2an/bN approche π.

Pour des aiguilles plus longues que l'écartement des lames (lorsque a>b), la formule obtenue est différente, mais fait toujous apparaitre π. Ainsi, dans le cas où a est beaucoup plus grand que b, la probabilité peut être approchée par p=1-b/πa.

Cette approximation de π qui nécessite énormement de lancers n'est pas très performante, mais on peut retenir l'idée. Cette méthode probabiliste de calcul approché est utilisée pour des calculs d'intégrale par un procédé portant le nom de Méthode de Monté Carlo.

"- Ben oui, les dalles extra-larges de la suite mesuraient 210 cm de large…
-...et les tailles respectives de vos victimes étaient de 160, 163, 166, 167, 167, 169, soit une moyenne de 165 centimètres.
- … vous êtes en train de voir les corps des malfrats comme des... aiguilles ?
Ils sont tous tombés à plat, raides morts ou grièvement blessés, et j’ai pu vérifier qu’exactement trois d’entre eux, sur les six que Cunégonde a abattus, se sont affalés au-dessus un joint latéral du dallage."
 

En considérant donc que les malfrats sont assimilables à des aiguilles (a=165 cm) tombant sur un carrelage (b=210 cm) et qu'un sur deux coupe un joint latéral, on obtient 3,14285 comme valeur pour le rapport 2an/bN censé approcher π.

La précision de l'aproximation de π obtenue ici est inespérée au vu du très faible nombre d'aiguilles. En pratique, pour obtenir une telle précision, il faut compter de l'ordre du million d’aiguilles (quelques milliers pour la première décimale) !