Calculs de probabilités
|
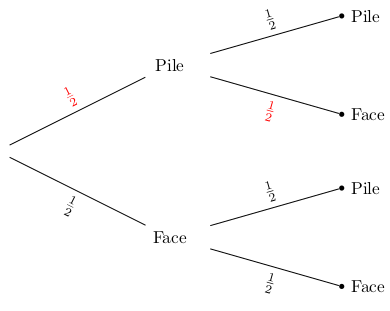
Un calcul de probabilité passe souvent par un dénombrement. Ainsi, lorsque les issues sont équiprobables, on calcule le rapport entre le nombre de cas favorables et le nombre de cas total. Par exemple, la probabilité de tomber sur pile en lancant une pièce est de 1/2 (les issues du lancer sont Pile et Face, au nombre de deux), de même la probabilité de tirer un As dans un jeu de 52 cartes est de 4/52=1/13 (les issues favorables sont les 4 As). Je vais considérer ici deux exemples de dénombrement suivant que l'on prend ou non en compte l'ordre. Cherchons la probabilité d'obtenir Pile puis Face en lancant deux fois une pièce, l'ordre est important. On peut avantageusement représenter la situation par un arbre comportant un noeud par lancer. En indiquant la probabilité sur chaque branche, la probabiité de chaque issue associé à une extrémité s'obtient en faisant le produit des probabilités -en rouge ci-dessous - à savoir 1/2x1/2=1/4.
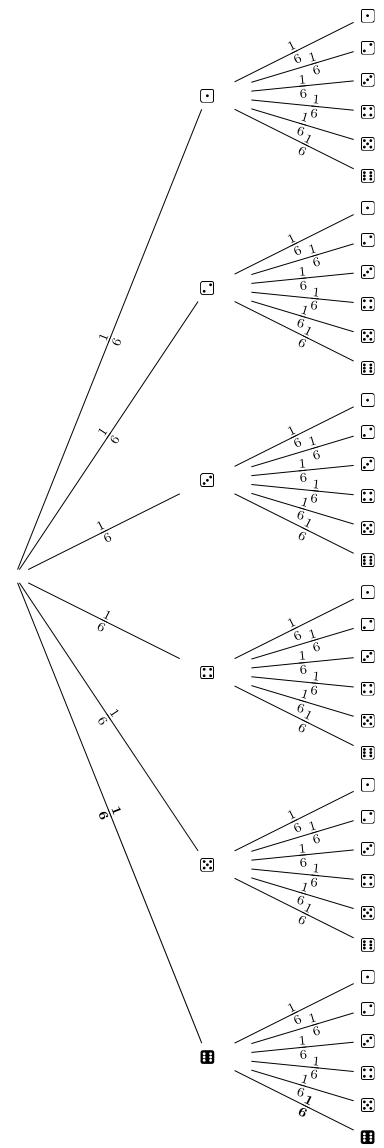
Cherchons maintenant le nombre de mains de deux cartes ne comportant que du coeur. Les deux cartes jouent le même rôle : il n'y a pas lieu de les ordonner. Néanmoins, par commodité du dénombrement, nous allons quand même arbitrairement ordonner les cartes et dresser un arbre. On a 13 choix possibles pour la première carte, puis 12 pour la seconde, ce qui fait 13x12 branches de l'arbre qui illustre les mains cherchées. Cependant, chaque main est ainsi comptée 2 fois en raison de l'ordre introduit : en effet, le tirage 7 de coeur puis 9 de coeurs et le tirage 9 de coeur puis 7 de coeur donnent la même main. Le nombre de mains cherché est donc 13x12/2 : on parle de combinaisons de 2 coeurs parmi 13. D'une manière analogue, le nombre de combinaisons de 3 coeurs parmi 13 est égale à (où 3!=3x2x1 est le nombre de toutes les permutations possibles de 3 cartes). Quant au nombre de mains de 2 cartes au total, il est de 52x51/2, à savoir le nombre de combinaisons de 2 cartes parmi 52, Pour finir, on peut dire que la probabilité d'obtenir une main sans coeur est donc Explicitons maintenant quelques exemples tirés du roman. P25. Le problème du chevalier de Méré : « Est-il aussi probable d’obtenir un 6 en lançant 4 fois un dé, ou d’obtenir un double 6 en lançant 24 fois deux dés ? » La clé pour se faciliter ici le calcul est de considérer l’événement contraire. Il est en effet bien plus facile de calculer la probabilité de n’obtenir aucun 6. Elle est de 5/6 à chaque lancer, ce qui donne (5/6)⁴=48,23 % de chances de n’obtenir aucun 6 en 4 lancers. On peut s'en convaincre en dressant un arbre à 4 branches, une par lancer). D’où, au contraire, nous avons 51,77 % de chances d’obtenir au moins un 6. Quant à la probabilité pour obtenir un double 6 en lancant deux dés, elle est bien de 1/36=1/6x1/6 comme illustré par l'arbre suivant :
|
P235 : "Et, pourtant, la chance d'avoir une main comportant au moins un as est de 14,93% seulement." (et non pas 14.79). Le calcul est encore une situation où la considération des événements contraires fait mouche. Dénombrons les mains sans aucun As. On tire 2 cartes parmi 48 (les 52 cartes auxquelles on a enlevé les 4 as), ce qui donne les combinaisons de 2 cartes pami 48, à rapporter aux combinaisons de 2 cartes parmi 52, c'est-à-dire
P17 Gévaudan se lamente de se retrouver avec un stack amputé de 100 euros en constatant se retrouver dans une situation se produisant moins d’une fois sur 250 000 000 (soit 4x10-9), Et de comparer avec d'autres probabilités particulièrement faibles. - Gagner 31 fois de suite à pile ou face, La probabilité est de (1/2)31, soit 1 chance sur 2 147 483 648. Il faut plutôt considérer 27 jeux de pile ou face successifs qui donnent 1 chance sur 134 217 728 ou encore une probabilité de 7.45x10-9. - Gagner le gros lot à l’Euromillion Il s'agit de trouver 5 numéros numérotés entre 1 et 50 et 2 étoiles numérotées de 1 à 12. Le nombre de tirages possibles est égal au nombre de combinaisons de 5 parmi 50 à multiplier par les combinaisons de 2 parmi 12. Soit une probabilité de gagner de 1 chance sur (50x49x48x47x46)/5! x(12x11)/2!=139 838 160. - Réunir au hasard 110 personnes sans aucun anniversaire commun, Ce calcul renvoit à ce qu'on appelle paradoxe des anniversaires. En effet, on peut établir qu'il y a plus de 50% de chances que dans un groupe de 23 personnes, au moins deux d'entre elle possèdent un anniversaire commun. Le terme de paradoxe vient du fait que ce faible nombre défie un peu l'intuition. Par commodité, on considèrera des années non bissextiles. On supposera aussi que l’hypothèse d’équiprobabilité est vérifiée - si on entreprend de vérifier expérimentalement ce paradoxe en TD en guise d'introduction au chapitre sur le dénombrement, on pourra s'assurer, d'un rapide coup d'oeil, que ne se trouve pas deux jumeaux dans l'assistance. Encore une fois, nous allons considérer l'événement contraire et dénombrer les situations où tous les annversaires sont différents. On peut ordonner arbitrairement les personnes et dresser un arbre avec une branche par individu. Il y a alors 365 possibilités pour le premier, puis 364 pour le deuxième (n’importe laquelle à l’exception de la date anniversaire du premier élève) puis 363 pour le troisième (n’importe laquelle à l’exception des dates anniversaire des deux premiers), etc... Dans le cas de n personnes, on obtient : 365!/(365-n)! possibilités. Ceci est à rapporter au nombre total de possibilités d'anniversaires : 365n (on a 365 possibilités par personne). La probabilité d'anniversaire commun est donc :
Pour n=23, la probabilité d'anniversaire commun est de 50.7%. Pour n=110, la probabilité qu'il n'y ait aucun anniversaire commun est d'environ 1.05x10-8. On peut pousser jusqu'à 112 personnes, pour obtenir une probabilité de 5.12x10-9. |