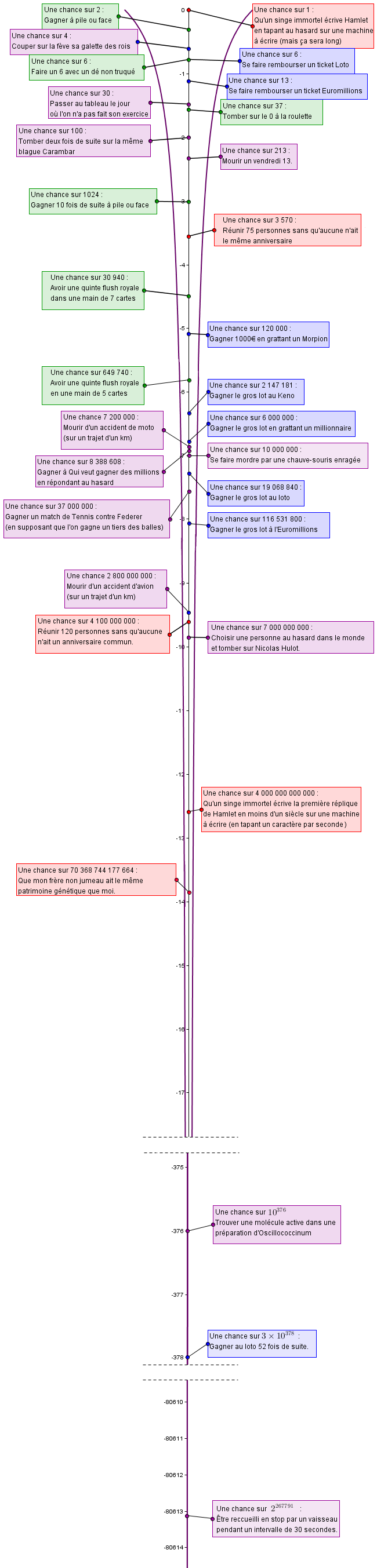
Probabilités improbables
|
Gévaudan se lamente de se retrouver avec un stack amputé de 100 euros en constatant se retrouver dans une situation se produisant moins d’une fois sur 250 000 000 (soit 4x10-9), Et de comparer avec d'autres probabilités particulièrement faibles : - Tomber 5 fois de suite sur la même blague Carambar (et non pas 150 fois comme cela est écrit !) En considérant qu'une centaine de blagues carambar différentes circulent à un moment donné (on peut se référer par exemple à l'ouvrage de J. Cottanceau), la probabilité de retomber 4 fois de suite sur la même blague qu'on a tirée une première fois est de (1/100)4=10-8.
- Gagner 27 fois de suite à pile ou face pour une probabilité de (1/2)27=7.45x10-9.
- Réunir au hasard 110 personnes sans aucun anniversaire commun, pour une probabilité de (365!)/(255)!)x(1/365)110 soit environ 10-8. - Gagner le gros lot à l’Euromillion Il s'agit de trouver 5 numéros numérotés entre 1 et 50 et 2 étoiles numérotées de 1 à 12. Le nombre de tirages possibles est égal au nombre de combinaisons de 5 parmi 50 à multiplier par les combinaisons de 2 parmi 12. Soit une probabilité de gagner de 1 chance sur (50x49x48x47x46)/5! x(12x11)/2!=139 838 160. Ce dénombrement est différent de 116 531 800 présenté dans la frise des probabilités ci-contre. Il se trouve qu'entre 2011 et 2016 les étoiles étaient seulement numérotées de 1 à 11.
- Que son Saint-Bernard et tous ses descendants lui écrivent le message « Pierre je taime » en supposant qu’ils parviennent à taper au hasard sur les touches d’un clavier adapté à raison d’une touche par seconde durant tout un millénaire... En faisant abstraction des espaces, on considère une machine à écrire rudimentaire comportant juste les 26 lettres de l'alphabet. On suppose que chaque touche possède la même probabilité d'être enfoncée par les saint-bernards. Obtenir la bonne combinaison de 13 lettres à la première tentative est de a=(1/26)13. Le nombre de lettres tappées pendant un millénaire est b=365x24x60x60 (en faisant abstraction des années bissextiles). Il faut enlever 13 à ce nombre pour obtenir le nombre de suites de 13 lettres à tester. La probabilité cherchée correspond alors au produit ab=1.27×10-8. Si on prend en compte les espaces dans le message, le clavier comporte alors 27 touches et le message obtenu est de 17 lettres. La probabilité devient alors 1.07×10-11. «Je ne suis qu’une conjonction de probabilités improbables.» Pour respecter les ordres de grandeur : « La probabilité pour le spermatozoïde qui m’a conçu de féconder l’ovule était de 1 sur 400 millions. Au plus profond de mon être, je représente mieux qu'une victoire au premier rang au Loto. » La concentration en spermatozoïdes d'un éjaculat varie de 0.04 à 0.2 millions par ml, pour un volume de l'ordre de 2 à 8 ml, on obtient envron 6 000 milliards de spermatozoïdes (parmi lesquels il est délicat d'estimer ceux qui participent véritablement à "la course à l'ovule"). « Le fait de mesurer la taille que je fais et de peser le poids que je pèse, aux microns près, fait de moi un être unique quand bien même nous serions 500 milliards d’hommes sur Terre. » En effet, il y a (52x51)/2 mains de 2 cartes, d'où la probabilité d'obtenir 1500 mains données est l'inverse de ((52x51)/2)1500, à savoir 1.53x10-4684. Dans le jeu Qui veut gagner des millions ? il s'agit de répondre à 15 questions avec, à chaque fois, 4 réponses proposées. On considère que l'on répond au hasard sans faire usage des différents jokers mis à disposition. La probabilité de gagner le gros lot est alors de (1/4)15. La différence avec la probabilité donnée dans la frise ci-contre vient de ce qu'à partir de 2016 le jeu comporte 15 questions au lieu de 12. Au final, on obtient pour 500 victoires : (1/4)15x500 soit 3.55x10-4516. |
Ci-dessous une frise des probabilités improbables tirée de improbabilités :
|