Probabilité conditionnelle et formule de Bayes

P106 "Étant donné deux événements A et B, la probabilité que B se réalise sachant que A est réalisé est traditionnellement notée P_A(B). Par exemple, la probabilité d’avoir deux filles est de 1 chance sur 4, par contre la probabilité d’avoir deux filles sachant que l’aînée est déjà une fille est de 1 chance sur 2."

Considérons que la probabilité d'avoir un garçon ou une fille soit la même (ce qui n'est pas rigoureusement exacte : en France on dénombre plutôt autour de 105 garçons pour 100 filles), pour une famille de deux enfants, on obtient l'arbre avec les probabilités suivantes :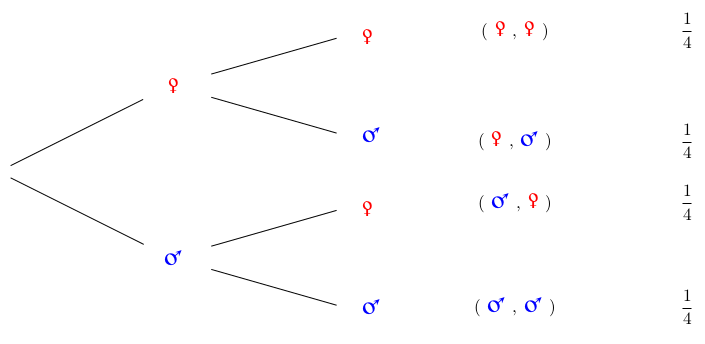

La première branche désigne l'aîné et la seconde branche le cadet.

La probabilité d'avoir deux filles est de 1/4.

Maintenant, si on ne considère que les fratries où l'âinée est une fille, on rejette toutes les situations où l'âiné est un garçon, il ne reste alors que deux branches (équiprobables) à l'arbre précédemment :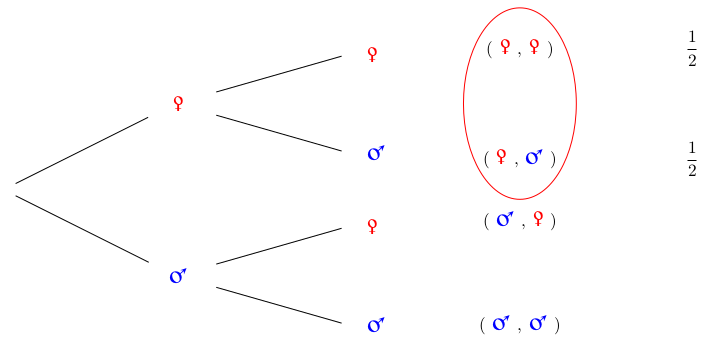

La probabilité d'avoir deux filles, sachant que l'aînée est une fille est donc de 1/2.

On aurait pu aussi ne considérer que les fratries où se trouve une fille, rejetter toutes celles où ne se trouve que des garçons, il resterait alors trois branches (équiprobables) du premier arbre considéré :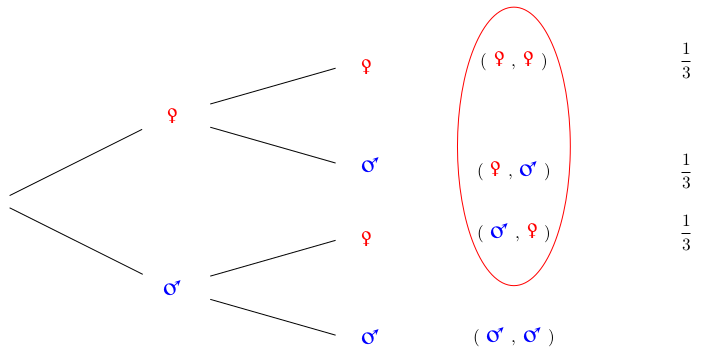

La probabilité d'avoir deux filles, sachant qu'il se trouve au moins une fille dans la fratrie est de 1/3.

P106-107

"La formule de Bayes stipule alors que le produit de la probabilité P_B(A) par P(B) est égal au produit de la probabilité P_A(B) par P(A).

De cette anodine formule naît un certain trouble lorsque l’événement B apparaît comme une conséquence de l’événement A puisqu’elle permet alors d’exprimer la probabilité d’une cause sachant sa conséquence... la formule de Bayes permet de remonter le temps !

Prenons l’exemple d’une maladie rare que l’on cherche à dépister. L’événement A est « être malade » et l’événement B « avoir un test positif ». Supposons que la maladie frappe 1 personne sur 10 000 et que le test de dépistage présente les caractéristiques suivantes : si une personne est malade, le test est positif à 99% ; si une personne n’est pas malade, le test est positif à 0,1%. Les deux premières conditions se traduisent par les égalités P(A)=0.01 % et P_A(B)=99 % et, à première vue, le test semble performant.

Renversons maintenant cause et conséquence. La formule de Bayes permet d’établir que la probabilité P_B(A) qu’une personne soit malade si son test est positif est de 9%. Il y a donc 91% de chances qu’une personne positive au test ne soit pas malade ! D’un coup, le test ne semble plus aussi performant. La formule de Bayes apprend à se méfier lorsque des probabilités faibles sont en jeu."

Si l'événement A est "être malade", nous notons $\overline{A}$ l'événement "ne pas être malade".

Nous disposons des valeurs

Nous pouvons en déduire la valeur de toutes les probabilités de l'arbre suivant qui décrit tous les cas de figure possibles, en commençant par la disjonction de cas A (être malade) et $\overline{A}$ (ne pas être malade) suivie de la disjonction de cas B (test positif) et $\overline{B}$ (test négatif). L'avantage d'une telle représentation est qu'elle permet d'associer chaque branche à une probabilité, notamment les secondes branches qui s'interprètent comme des probabilités conditionnelles. Par ailleurs, le produit des probabilités en suivant une même branche donne la probabilité de la conjonction des événements correspondants.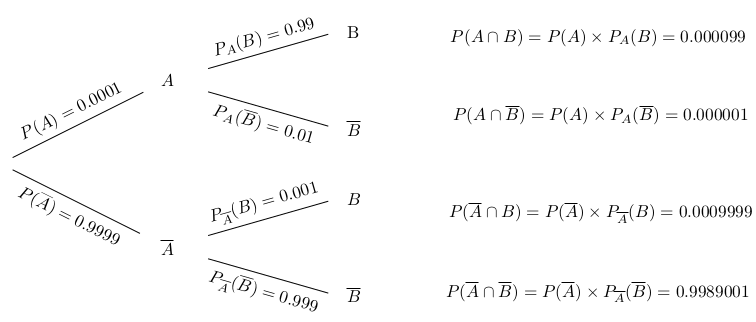

Pour répondre à la question posée, à savoir déterminer la probabilité P_B(A), il s'agit de calculer les probabilités associées au nouvel arbre où on présente en premier la disjonction $(B,\overline{B})$ et ensuite la disjonction $(A,\overline{A})$. En fait, nous ne sommes intéressés que par la branche supérieure.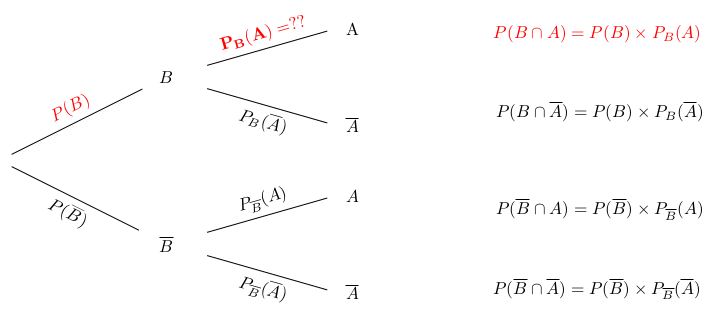

Nous connaisons déjà du premier arbre la valeur de $P(B\cap A)=P(A\cap B)=0.000099$ . Reste à déterminer la valeur de P(B). Elle peut aussi se déduire du premier arbre en considérant que

  ${\displaystyle P\left(B\right)=P(B\cap A)+P(B\cap \overline{A})=P\left(A\right)\times P_A\left(B\right)+P\left(\overline{A}\right)\times P_{\overline{A}}\left(B\right)}$  

formule dite des probabilités totales. Dans l'idée, on retient chaque branche de l'arbre qui passe par une feuille étiquetée B.

Cela donne P(B)=0.000099+0.009999=0,0010989.

De la formule $P_B\left(A\right)\times P\left(B\right)=P(A\cap B)$ on tire alors la valeur

P_B(A)=0,09009009. La probabilité qu’une personne soit malade si son test est positif est donc de l'ordre de 9%.