Le jeu de Monty Hall
|
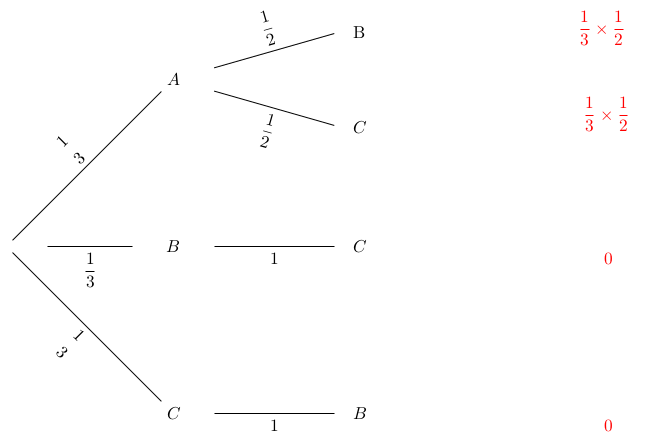
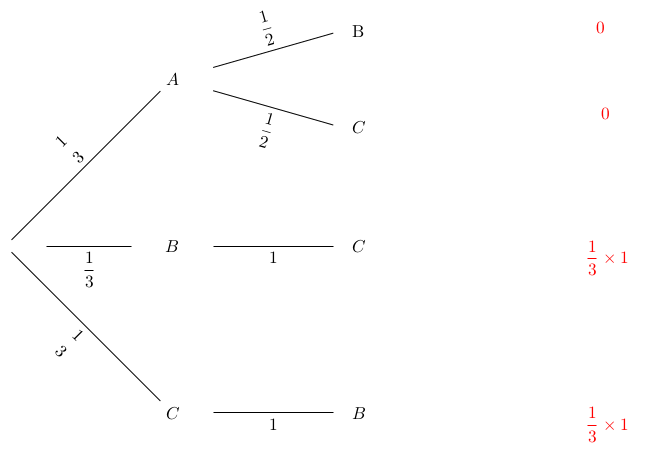
P84. Le principe du jeu Un lot est caché derrière une des trois portes présentée à un candidat. Ce dernier désigne - au hasard - une des trois portes et l'animateur, qui sait où se cache le lot lui ouvre une des deux portes restantes où ne se trouve pas le lot. Le candidat a alors le choix de garder la porte choisie initialement ou de changer pour ouvrir l'autre porte qui reste. Ce jeu défie un peu l’intuition, car la plupart des gens pensent que, étant donné qu'il reste deux portes en jeu, il y a 1 chance sur 2 de gagner le lot en gardant la porte choisie au départ et 1 chance sur 2 de gagner en changeant de porte. Ce raisonnement est erroné car il y a en fait 2 chances sur 3 de gagner en changeant de porte. Plusieurs arguments sont présentés dans l'ouvrage. Je vais ici donner l'idée d'un autre raisonnement qui passe par les probabilités contraires - multiplier les arguments est le meilleur ressort pour faire passer une idée allant à l'encontre des premières intuitions. Considérons (encore !) l'événement contraire, à savoir la probabilité de perdre. Le choix initial donne 2 chances sur 3 de perdre, ce qui correspond à la probabilité de perdre au bout du compte si l'on ne change pas de porte. Il faut donc bien changer de porte ! De manière plus standard, nous pouvons aussi illustrer la situation à l'aide d'un arbre. Pour fixer les idées, supposons que le lot à gagner soit caché derrière la porte A. La première branche de notre arbre désigne le choix du candidat (équiprobable entre les portes A,B,C). Puis, la deuxième branche de l'arbre désigne la porte ouverte par le présentateur. Au final, à l'extrémité des branches de l'arbre, nous pouvons lire la probabilité de gagner. D'abord, avec la stratégie de conserver la porte, nous obtenons une probabilité de gagner de 1/6+1/6=1/3.
Puis, avec la stratégie de changer la porte, nous obtenons une probabilité de gagner de 1/3+1/3=2/3.
|
Monty Hall et les pigeons La version du jeu pour les pigeons est tirée d'un article de Herbranson et Schroeder : Are Birds Smarter Than Mathematicians? On pourra aussi consulter le site sciencetonnante. Y est tiré notamment la conclusion que les pigeons s'adaptent mieux que l'être humain face à la répétition du problème. Pollué par sa mauvaise intuition, l'homme continuerait de penser que changer de porte ou non ne fait pas de différence, au contraire du pigeon. Les deux enveloppes : une autre affaire de choix ? Il existe un paradoxe classique qui fait aussi appel à un choix de garder ou de changer, mais dont le ressort et les conclusions ne sont pas du tout les mêmes. La situation est la suivante. On propose à un candidat deux enveloppes qui contiennent chacune une somme d'argent. Lorsque le candidat a ouvert son enveloppe, on lui dit que l'une des enveloppe contient le double de l'autre. Il a alors le choix de garder l'enveloppe qu'il vient de prendre ou alors de choisir l'autre enveloppe à la place. Pour fixer les idées, supposons que la première enveloppe contienne 100€. On lui dit qu'il aurait tout intérêt à changer car il y a 1 chance sur 2 que la deuxième enveloppe contienne 50€ et 1 chance sur 2 qu'elle contienne 200€. Dans le premier cas, il perdrait 50€, dans le second, il gagnerait 100€, ce qui donnerait une espérance de gain globale de +25€, d'où l'intérêt de changer d'enveloppe. Convainquant ? Là où cela se complique c'est que, contrairement au cas du jeu de Monty Hall où l'animateur apporte une vraie information après le choix du candidat, ici l'information donnée aurait tout aussi bien être fournie dès le début du jeu. En fait, on peut tenir le résultat simple suivant : dès le premier choix on a 1 chance 2 de tomber sur l'enveloppe la plus fournie et le fait de changer d'enveloppe ne modifie pas cette probabilité. En termes plus mathématiques, on peut dire que les enveloppes contiennent respectivement une somme de M et 2M. On fait un arbre à deux feuilles M et 2M - avec probabilité 1/2 sur chaque branche - qui représente le choix du candidat, et on peut calculer l'espérance de gain : on trouve 3M/2 que l'on garde l'enveloppe ou qu'on en change. Problème ! Où est le biais ? Il se trouve dans la manière de présenter les choses dans le premier raisonnement qui suppose que le choix est équiprobable entre les paires d'enveloppes {M,2M} et {M/2,M}. Or ceci est impossible. En effet, il faudrait déjà pour cela disposer d'un nombre infini de paires d'enveloppes (par exemple l'ensemble des paires {2^k,2^{k+1}) où k décrit les entiers relatifs). Sur un tel univers, on ne peut pas espérer une équiprobabilité. On peut néanmoins s'amuser à modifier légèrement les conditions de l'expérience. On propose un choix parmi 10 paires d'enveloppes qui contiennent les sommes {1,2},{2,4},{4,8},...,,{512,1024} : hormis 1 et 1024, une même somme se trouvent dans deux enveloppes. Une fois choisie la paire d'enveloppes, le candidat tire une des deux enveloppes et révèle la somme qu'elle contient. Si on lui donne l'information que cette somme n'est pas la somme maximale dans le jeu, alors il a intérêt à changer d'enveloppe. Quand bien même la somme maximale ne sera tirée qu'une fois sur 20, cette information suffit à justifier la stratégie de changer d'enveloppe. |
On peut s'amuser à modifier les conditions du jeu. En considérant toujours qu'il n'y a qu'un seul lot, notons n le nombre de portes total, c1 le nombre de portes qu'on peut choisir au début, e le nombre de portes que l'animateur ouvre en fonction et c2 le nombre de portes qu'on peut ouvrir si on décide de changer (auquel cas on ne garde aucune des portes choisies au départ). On a donc n qui vaut au moins c1+c2+e.