CMAGXX une application MODULEF pour le calcul du champ magnétique induit par un objet uniformément aimanté.

Nous avons développé un code de calcul organisé autour de la structure de programmes MODULEF pour résoudre le problème de magnétostatique suivant: calculer le champ magnétique induit par un objet métallique, constitué d'un matériau paramagnétique, soumis à une induction magnétique uniforme .
Cette application nécessite le logiciel  d'éléments finis MODULEF pour fonctionner.  MODULEF peut être obtenu gratuitement auprès de L'INRIA Rocquencourt à l'adresse http://www-rocq.inria.fr/modulef/
 

Si $\Omega$ désigne le domaine de $\mathbb{R} ^3$ occupé par l'objet, le problème s'écrit en termes d'équations aux dérivées partielles: trouver  et  vérifiant

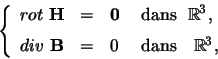$$\left\{\begin{array}{ccll}rot\ \ensuremath{\mathbf{H}} &=&...... 0 & \mbox{\ dans \ }\ \mathbb{R} ^3 ,\\\end{array}\right .$$ (1)

avec pour condition à l'infini

$$\lim_{\vert x\vert \rightarrow \infty}\ensuremath{\mathbf{B}} (x)= \ensuremath{\mathbf{B_0}} .$$ (2)

Les champs  et  sont liés au vecteur aimantation  par la relation $\dps \ensuremath{\mathbf{B}} = {\mu_0} (\ensuremath{\mathbf{H}} + \ensuremath{\mathbf{M}} )$. Pour un milieu paramagnétique,  et  sont liés par une loi de comportement linéaire. Nous supposons ici que le milieu $\Omega$ est uniformément aimanté avec une aimantation donnée par

$$\ensuremath{\mathbf{M}} = \frac{\chi_m}{\mu_0}\ \ensuremath{\mathbf{B_0}} ,$$ (3)

où la constante $\chi_m$ est la susceptibilité magnétique du matériau.
 
 

Nous avons établi et étudié une méthode de calcul de l'induction magnétique secondaire (ou de réaction) $\ensuremath{\mathbf{B'}} = \ensuremath{\mathbf{B}} - \ensuremath{\mathbf{B_0}}$spécifique à ce problème. La nécessité d'écrire un code de calcul bien adaptée à ce problème plutôt que d'utiliser des codes plus généraux de calcul en électromagnétisme nous est apparu lors de l'étude des artefacts de susceptibilité magnétique en Imagerie par Résonnace Magnétique (IRM). Dans ce cas précis, l'objet $\Omega$ est un implant médical métallique et l'induction magnétique  est celle engendrée par l'aimant de l'imageur et utilisée pour obtenir l'image IRM. Si l'on souhaite simuler numériquement les artefacts de susceptibilité magnétique, il faut être en mesure de calculer de manière rapide et précise le champ induit sur un maillage très fin autour de l'implant. De plus, les résultats de ce calcul doivent être facilement utilisables par le code de reconstruction de l'artefact.
 
 

La méthode de calcul de l'induction magnétique $\ensuremath{\mathbf{B'}}$ est basée sur une formule de représentation intégrale. À partir des résultats classique de la théorie du potentiel, nous montrons, voir [Balac97], que l'induction magnétique secondaire solution du problème (1) s'écrit,

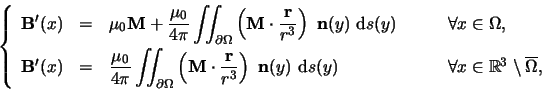$$\left\{\begin{array}{ccll}\ensuremath{\mathbf{B}} '(x) &=&......athbb{R} ^3\setminus\overline{\Omega} , \\\end{array}\right.$$ (4)

où $\ensuremath{\mathbf{r}} = x - y$. Dans la situation qui nous intéresse l'aimantation  est constante et connue. Le calcul de l'induction magnétique secondaire se ramène donc au calcul d'une intégrale surfacique.

Lorsque la frontière $\Sigma$ du domaine $\Omega$ est formée (ou possède) des faces planes, il est possible de calculer l'intégrale dans (4) de manière exacte. Lorsque la surface $\Sigma$ possède des portions non planes, un calcul analytique de l'intégrale sur ces portions n'est plus envisageable. L'idée consiste alors à effectuer un maillage de la surface $\Sigma$ à l'aide de triangles et à approcher $\Sigma$ par interpolation d'ordre deux à partir de la triangulation. On obtient alors une surface approchée $\Sigma_h$ formée de triangles courbes (des morceaux de quadriques). On décompose l'intégrale sur $\Sigma_h$ en une somme d'intégrales sur chacun des triangles courbes. L'intégrale sur chaque triangle est calculée en utilisant une formule de quadrature numérique. Nous avons établi que l'erreur d'approximation se comporte en O(h⁴), hdésignant le pas du maillage de la surface. Lorsque le point P est très proche de la surface (en pratique si la distance de Pà $\Sigma$ est plus petite que $3\ h$) on est confronté à un comportement quasi-singulier de l'intégrale. Pour traiter cette singularité numérique nous avons adapté une méthode utilisée par K.E. Atkinson dans son code de résolution d'équations intégrales de surface [Atkinson89].
 
 

Les deux méthodes de calcul de l'intégrale qui viennent d'être décrite sont utilisées conjointement dans notre code de calcul. Les différentes étapes permettant le calcul de l'induction magnétique sont les suivantes.

• On effectue une triangulation de la surface $\Sigma$ de l'implant.
• Dans le cas où la surface $\Sigma$ est courbe, on construit la surface approchée $\Sigma_h$ obtenue par interpolation d'ordre deux à partir de la triangulation.
• On calcule les intégrales sur chaque triangle de la triangulation, soit analytiquement, soit numériquement.

Nous présentons la méthode de calcul de l'intégrale et le programme CMAGXX mettant en oeuvre la méthode.