Pour calculer l'intégrale sur ![]() nous
utilisons une méthode analytique. Nous tirons profit du fait que
dans ce cas particulier la normale
nous
utilisons une méthode analytique. Nous tirons profit du fait que
dans ce cas particulier la normale ![]() est constante sur chaque triangle. Pour
obtenir la valeur de
est constante sur chaque triangle. Pour
obtenir la valeur de ![]() au point
au point ![]() , il suffit de calculer pour chaque triangle K
de la triangulation appartenant à
, il suffit de calculer pour chaque triangle K
de la triangulation appartenant à ![]() ,
l'intégrale
,
l'intégrale
Désignons par Q1,Q2,Q3
les sommets du triangle K. On note Q0 la
projection du point P sur le plan défini par K.
Nous introduisons les triangles K1, K2
et K3, (voir la Figure 1), de sommets respectifs ![]() et
et ![]() . Nous décomposons
alors l'intégrale sur K en la somme de trois
intégrales sur les triangles K1, K2
et K3
. Nous décomposons
alors l'intégrale sur K en la somme de trois
intégrales sur les triangles K1, K2
et K3
Intéressons-nous au calcul de l'intégrale sur le
triangle Kk de sommets ![]() où
où ![]() et
et ![]() ,
, ![]() . Nous
introduisons un nouveau repère
. Nous
introduisons un nouveau repère ![]() associé au triangle Kken
prenant pour origine Q0 et pour vecteurs de la base
orthonormée
associé au triangle Kken
prenant pour origine Q0 et pour vecteurs de la base
orthonormée
Dans ce nouveau repère les sommets ont pour
coordonnées
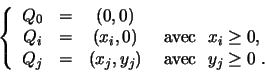
Soit (x,y) les coordonnées du point
générique Q dans le repère ![]() et soit
et soit ![]() .
Nous avons
.
Nous avons ![]() Par
conséquent les composantes de l'intégrale
Par
conséquent les composantes de l'intégrale 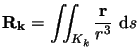 dans
le repère
dans
le repère ![]() sont
sont
| R1 | = | 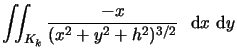 |
|
| = | 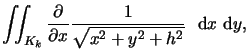 |
||
| R2 | = | 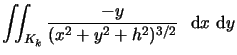 |
(8) |
| = | 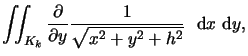 |
||
| R3 | = | 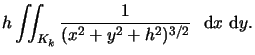 |
Le calcul de ces intégrales est effectué dans
[Balac97]. Posons
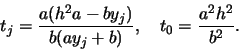
| F(a,b,u) | = | 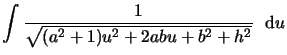 |
|
| = | 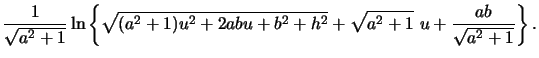 |
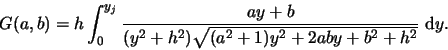
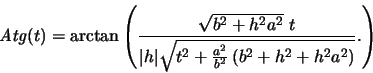
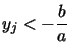 ,
, 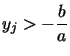 ,
, 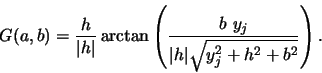
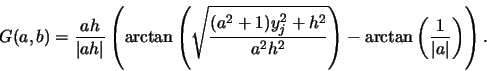
On a alors les expressions suivantes pour les composantes de
l'intégrale 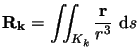 dans
le repère
dans
le repère ![]() ,
,
On obtient alors ![]() donnée par (7)
en calculant
donnée par (7)
en calculant ![]() pour k=1,2,3
par les formules (9), puis en
sommant ces trois termes après avoir exprimé les vecteurs
pour k=1,2,3
par les formules (9), puis en
sommant ces trois termes après avoir exprimé les vecteurs ![]() dans la base d'origine.
dans la base d'origine.