Présentation de la méthode de calcul de l'induction

Nous souhaitons calculer l'induction magnétique secondaire pour un implant métallique paramagnétique d'aimantation constante à partir des formules de représentation intégrale (4). Il s'agit de calculer l'intégrale surfacique

$$\mathcal{I}(x) = \int\!\!\!\int_{\Sigma} \left( \ensuremath{\... ...}} }{r^3} \right) \ensuremath{\mathbf{n}} (y) \mbox{ d}s (y) .$$ (5)

Nous considérons une triangulation ${\mit T_h}$ de la surface $\Sigma$, c'est-à-dire une décomposition de $\Sigma$ en une réunion finie de triangles K,

$$\Sigma = \bigcup_{K\in {\mit T_h}} K ,$$

telle que,

• deux triangles ont leur intersection qui est soit vide, soit réduite à un sommet commun, soit réduite à une arête commune;
• toute arête est contenue dans exactement deux triangles distincts.

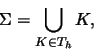
Nous distinguons les deux cas suivants:

• $\Sigma$ (ou une partie de $\Sigma$) est formée de surfaces planes,
• $\Sigma$ (ou une partie de $\Sigma$) est formée de surfaces courbes.

Nous adoptons une méthode de calcul de l'intégrale spécifique pour chacun de ces deux cas. Nous notons $\Sigma_p$ la partie de $\Sigma$ constituée de surfaces planes et $\Sigma_c$ la partie de $\Sigma$ constituée de surfaces courbes (non-planes). On a

$$\mathcal{I}(x) = \int\!\!\!\int_{\Sigma_p} \left( \ensuremat... ...}} }{r^3} \right) \ensuremath{\mathbf{n}} (y) \mbox{ d}s (y) .$$ (6)

L'intégrale sur $\Sigma_p$ est calculée de manière exacte. Pour calculer l'intégrale sur $\Sigma_c$ nous avons recours à une intégration numérique. Nous décrivons ces deux méthodes.
 

• Calcul de l'intégrale de surface pour les parties planes
• Calcul numérique de l'intégrale de surface