| |
(9) |
La méthode de calcul de cette intégrale consiste
à approcher la surface ![]() par une
surface
par une
surface ![]() obtenue par interpolation quadratique
par morceaux à partir d'un maillage de la surface
obtenue par interpolation quadratique
par morceaux à partir d'un maillage de la surface ![]() . On décompose l'intégrale sur
. On décompose l'intégrale sur ![]() en une somme d'intégrales sur les triangles
en une somme d'intégrales sur les triangles ![]() formant la surface
formant la surface ![]() . La
normale
. La
normale ![]() est approchée par la normale
au triangle
est approchée par la normale
au triangle ![]() et
l'intégrale est évaluée à l'aide d'une
formule de quadrature numérique.
et
l'intégrale est évaluée à l'aide d'une
formule de quadrature numérique.
On suppose que ![]() est l'image d'un domaine D polygonal fermé de
est l'image d'un domaine D polygonal fermé de
![]() par un
par un
![]() -difféomorphisme
F,
-difféomorphisme
F,
![]() .
.
Pour chaque domaine D, on introduit une triangulation
![]() de D au sens des triangulations usuelles en
éléments finis,
de D au sens des triangulations usuelles en
éléments finis,
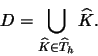
Remarque: s'il n'existe pas de
![]() -difféomorphisme F tel que
-difféomorphisme F tel que
![]() ,
il est possible de décomposer la surface
,
il est possible de décomposer la surface ![]() en J morceaux
en J morceaux
![]() pour lesquels
pour lesquels ![]() est l'image d'un domaine Djpolygonal fermé de
est l'image d'un domaine Djpolygonal fermé de
![]() par un
par un
![]() -difféomorphisme
Fj.
-difféomorphisme
Fj.
On désigne par
![]() l'élément générique de la triangulation
l'élément générique de la triangulation
![]() .
Ses sommets sont notés
.
Ses sommets sont notés
![]() et
et
![]() .
Sans restreindre la généralité, on supposera que D est un triangle
rectangle isocèle.
.
Sans restreindre la généralité, on supposera que D est un triangle
rectangle isocèle.
On obtient une triangulation ![]() de la surface
de la surface ![]() en prenant
l'image par F de la triangulation
en prenant
l'image par F de la triangulation
![]() de D.
L'image du triangle
de D.
L'image du triangle
![]() par l'application F est noté K.
On note S1, S2 et S3 ses sommets qui sont définis par
par l'application F est noté K.
On note S1, S2 et S3 ses sommets qui sont définis par
![]() .
.
Soit ![]() le triangle de référence
le triangle de référence
| (10) |
| (11) |
Pour approcher la surface ![]() on remplace l'application F,
pour chaque triangle
on remplace l'application F,
pour chaque triangle ![]() , par
, par ![]() l'interpolant de Lagrange de
degré 2 sur
l'interpolant de Lagrange de
degré 2 sur ![]() . L'interpolant
. L'interpolant ![]() vérifie
vérifie
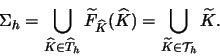 |
(14) |
Nous avons
![]() donnée par (10) qui s'écrit
donnée par (10) qui s'écrit
| = | 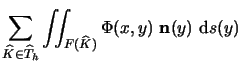 |
||
| = | 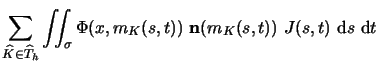 |
(15) |
| (16) |
Il est en général mal aisé pour une surface ![]() quelconque
d'expliciter l'application mK et de calculer J.
Pour pouvoir calculer
quelconque
d'expliciter l'application mK et de calculer J.
Pour pouvoir calculer
![]() ,
nous avons donc recours à l'interpolant
,
nous avons donc recours à l'interpolant
![]() d'ordre 2 de mK donné en (14).
Ceci nous amène à considérer l'approximation suivante de
d'ordre 2 de mK donné en (14).
Ceci nous amène à considérer l'approximation suivante de
![]() ,
,
| (18) |
| (19) |
Il n'est pas possible de calculer l'intégrale dans (18) de
manière exacte.
Nous utilisons une méthode d'intégration numérique.
Nous avons mis en évidence que des difficultés numériques liées
à l'utilisation d'une formule de quadrature numérique apparaissaient
quand le point x se situait à proximité de la surface ![]() .
Bien que les intégrales ne soient pas à proprement parler singulières,
la précision de l'évaluation numérique se dégrade sérieusement
en raison de la grande rapidité des variations de l'intégrant au voisinage
de la surface (il se comporte en fonction de la distance à la surface r,
comme r-2).
.
Bien que les intégrales ne soient pas à proprement parler singulières,
la précision de l'évaluation numérique se dégrade sérieusement
en raison de la grande rapidité des variations de l'intégrant au voisinage
de la surface (il se comporte en fonction de la distance à la surface r,
comme r-2).
Ce type d'intégrales quasi-singulières se retrouve lors de
la mise en ![]() uvre des méthodes d'équation intégrale de frontière.
Deux approches sont possibles afin de calculer avec précision les
intégrales singulières [#!Huang93!#].
La première consiste à utiliser des transformations géométriques
(changements de variables) afin d'affaiblir la singularité.
La seconde consiste à augmenter le nombre de n
uvre des méthodes d'équation intégrale de frontière.
Deux approches sont possibles afin de calculer avec précision les
intégrales singulières [#!Huang93!#].
La première consiste à utiliser des transformations géométriques
(changements de variables) afin d'affaiblir la singularité.
La seconde consiste à augmenter le nombre de n![]() uds de quadrature, soit en
augmentant l'ordre de la formule de quadrature,
soit en divisant le domaine d'intégration.
Nous avons adopté cette dernière solution, en raison de la simplicité de
sa mise en
uds de quadrature, soit en
augmentant l'ordre de la formule de quadrature,
soit en divisant le domaine d'intégration.
Nous avons adopté cette dernière solution, en raison de la simplicité de
sa mise en ![]() uvre et de son efficacité.
Nous reprenons une méthode introduite par K.E. Atkinson dans
[#!Atkinson85b!#], [#!Atkinson89!#].
Cette méthode consiste à distinguer deux types de formules de quadrature
en fonction de la distance du point P au triangle
uvre et de son efficacité.
Nous reprenons une méthode introduite par K.E. Atkinson dans
[#!Atkinson85b!#], [#!Atkinson89!#].
Cette méthode consiste à distinguer deux types de formules de quadrature
en fonction de la distance du point P au triangle
![]() sur lequel
doit être évaluée l'intégrale.
sur lequel
doit être évaluée l'intégrale.
Pour calculer
- Si
Si ![]() , alors
l'intégrant est considéré comme étant
régulier (on veut dire par là que ni l'intégrant,
ni ses dérivées n'ont de fortes variations ou ne
deviennent très grands). Dans ce cas, on utilise la formule de
quadrature à trois points, du second ordre,
, alors
l'intégrant est considéré comme étant
régulier (on veut dire par là que ni l'intégrant,
ni ses dérivées n'ont de fortes variations ou ne
deviennent très grands). Dans ce cas, on utilise la formule de
quadrature à trois points, du second ordre,
- Si ![]() , alors l'intégrant
est de type "quasi-singulier"; lorsque le point x est pris
proche d'un triangle
, alors l'intégrant
est de type "quasi-singulier"; lorsque le point x est pris
proche d'un triangle ![]() , l'intégrant devient très grand
et varie dans de grandes proportions en fonction du point
, l'intégrant devient très grand
et varie dans de grandes proportions en fonction du point ![]() . La méthode d'intégration
doit être à même de prendre en compte ce
comportement quasi-singulier de l'intégrant. Nous avons recours
à la formule de quadrature à sept points, d'ordre 5,
référencée (T2:5-1) dans [#!Stroud71!#] p.
314,
. La méthode d'intégration
doit être à même de prendre en compte ce
comportement quasi-singulier de l'intégrant. Nous avons recours
à la formule de quadrature à sept points, d'ordre 5,
référencée (T2:5-1) dans [#!Stroud71!#] p.
314,
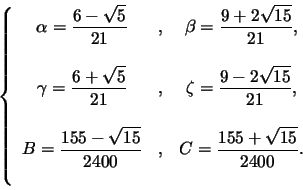
Les valeurs des paramètres Nd et ![]() sont fixées de manière empirique.
sont fixées de manière empirique.