Tests statistiques usuels
A partir des résultats d'estimation avec la méthode des Moindres Carrés Ordinaires d'un modèle de régression linéaire simple ou multiple on peut effectuer différents tests statistiques.
Ils portent sur la valeur des paramètres et sur les propriétés des aléas. L'objectif est de réaliser des tests pour valider les résultats d'un point de vue statistique mais aussi pour analyser les résultats d'un point de vue économique.
- Test de contraintes sur les paramètres
- Test de stabilité des paramètres
- Test de normalité des aléas
- Tests d'homoscédasticité des aléas
- Tests de non autocorrélation des aléas
- Test d'erreurs de mesure
Il existe par ailleurs des tests plus spécifiques liés à l'utilisation de l'estimateur des variables instrumentales
Les tests de contraintes sont basés sur la distribution d’une part de l’estimateur des MCO et d’autre part de la variance estimée des aléas. Les tests d'une contrainte sont des tests de Student, en revanche, les tests de plusieurs contraintes sont des tests de Fisher.
C Test d'une contrainte
Pour tester une contrainte linéaire de la forme r’B=q avec r de dimension (K,1) et q un scalaire on calcule la statistique de Student suivante :
![]() avec un risque
a
de 5% ou 10%
avec un risque
a
de 5% ou 10%
Si la
statistique calculée est plus faible en valeur absolue que la valeur tabulée on
accepte l’hypothèse nulle
![]() , l’hypothèse alternative étant
, l’hypothèse alternative étant
![]()
Le test de significativité des paramètres du modèle est un cas particulier de ce test.
C Test de plusieurs contraintes
Pour effectuer un
test de plusieurs contraintes tel que
![]() avec R une matrice d’ordre (J,K) , J correspondant au nombre
de contraintes, on doit calculer la statistique de Fisher suivante :
avec R une matrice d’ordre (J,K) , J correspondant au nombre
de contraintes, on doit calculer la statistique de Fisher suivante :
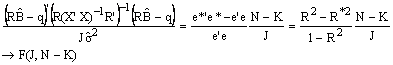
avec e le vecteur des résidus du modèle estimé sans les contraintes et R2 son coefficient de détermination, et e* le vecteur des résidus du modèle estimé avec les contraintes et R*2 son coefficient de détermination. L'hypothèse nulle est acceptée lorsque la statistique calculée est inférieure à la valeur tabulée. Les tests de modèles emboîtés et de significativité globale de la régression utilisent cette procédure de test.
APPLICATIONS
:
Analyse de l’investissement en France sur la période 1970-1998,
Analyse de la demande d’essence aux Etats-Unis entre 1960-1995
Le test de chow est le test standard, il propose de tester la stabilité du modèle pour une date fixée, connue à priori. En revanche les tests de stabilité basés sur les résidus récursifs cherchent à détecter la présence d'une date de rupture.
C Test de Chow
Le test de Chow peut s'écrire sous la forme d'un test de plusieurs
contraintes. On considère une date susceptible d'avoir induit une modification
de l'équation de comportement, on note n0 cette date et on cherche à
tester si les paramètres sont identiques sur l'ensemble de la période 1,..,N ou
si les paramètres sont différents sur les sous- périodes 1,..n0 et n0+1,..N,
autrement dit on effectue le test suivant :
![]() avec B1 le vecteur de paramètre sur la première période et B2 le vecteur sur la seconde. Sous l’hypothèse nulle il y a
stabilité, il s'agit d'un modèle avec K contraintes car chaque paramètre doit
être identique sur les deux sous-périodes. Sous l'hypothèse alternative, on a un
modèle sans contraintes, il faut dans ce cas estimer le modèle sur les deux
sous-périodes pour obtenir 2K paramètres estimés.
avec B1 le vecteur de paramètre sur la première période et B2 le vecteur sur la seconde. Sous l’hypothèse nulle il y a
stabilité, il s'agit d'un modèle avec K contraintes car chaque paramètre doit
être identique sur les deux sous-périodes. Sous l'hypothèse alternative, on a un
modèle sans contraintes, il faut dans ce cas estimer le modèle sur les deux
sous-périodes pour obtenir 2K paramètres estimés.
On calcule la statistique de Fisher :
![]()
La somme des carrés des résidus e*'e* est déduite de l'estimation de l'équation sur l'ensemble de la période et la somme des carrés des résidus e'e correspond à la somme de la somme des carrés des résidus de l'estimation sur chaque sous période.
Si la statistique calculée est inférieure à la valeur tabulée on accepte l’hypothèse de stabilité. La date n0 ne constitue pas une date de rupture, il n’y a pas de changement structurel.
C Test de stabilité basé sur les résidus récursifs
Pour calculer les résidus récursifs on doit estimer le modèle de régression linéaire pour un nombre d'observations r allant de K à N.
Soit er l’erreur de prévision ex-post sur
l’observation yr : ![]() avec :
avec :
![]() et
et ![]() le paramètre
le paramètre ![]() estimé avec un nombre d’observations égale à r-1.
estimé avec un nombre d’observations égale à r-1.
L’espérance de cette erreur est nulle et sa variance est donnée par :
![]()
On définit les résidus
récursifs wr
de la manière suivante :![]()
Le test du CUSUM consiste à représenter graphiquement la série cumulée de ces
résidus :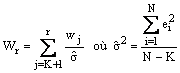
Pour un risque
a=5%, la région de confiance du test du CUSUM est
donnée par :
![]()
Le test du CUSUM of Square donne une représentation
graphique de la série suivante : 
Pour tester la stabilité on regarde si la série Sr
reste compris entre deux
droites tracées
parallèlement dont les équations sont :![]() où
où
![]() = r-K/N-K et c0
est une valeur
= r-K/N-K et c0
est une valeur
déterminée en fonction de K et N (la table correspondante peut-être trouvée dans
Johnston et Dinardo).
Pour effectuer les tests de contraintes on suppose au préalable que les aléas sont distribués selon une loi normale. Cette hypothèse peut-être testée avec la statistique de Jarque Béra. La procédure est la suivante:
- On estime le modèle avec la méthode des MCO
- On calcule les coefficients d'asymétrie (skewness) et d'aplatissement (Kurtosis) des résidus
- On calcule la statistique de Jarque-Bera:
avec
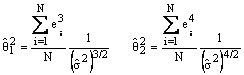
cette statistique suit une distribution du
à 2 degrés de liberté et pour une valeur calculée inférieure à la valeur tabulée on accepte l’hypothèse nulle de normalité.
Si l'hypothèse d'homoscédasticité n'est pas satisfaite l'estimateur des MCO n'est pas efficace. Il reste non biaisé mais il n'est plus BLUE, il existe un estimateur plus précis sans biais des paramètres : l'estimateur des Moindres Carrés Pondérés (estimateur des MCG dans le cas de l'hétéroscédasticité). Dans les tests d'homoscédasticité l'hypothèse nulle s'écrit :
![]()
C Test de White
Le test de White est un test asymptotique dans lequel il n'est pas nécessaire de spécifier les variables à l'origine de l'hétéroscédasticité. Si le modèle est de la forme
on doit :
- Estimer l'équation avec les MCO et en déduire les résidus ei
- Estimer la relation suivante :
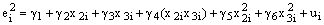
avec ui un aléa (de manière générale on utilise en variable explicative les variables en niveau, le produit des variables et les variables au carré)- On calcule la statistique NRe2, le coefficient de détermination étant le coefficient de détermination du modèle estimé lors de l'étape 2.
On ne rejette pas l'hypothèse nulle si la statistique NRe2 est inférieure à la valeur tabulé d'un c2 à 5 degrés de liberté, le degré de liberté est égal au nombre de paramètres estimés lors de la seconde étape moins un.
CTest de Golfeld et Quandt
Ce test est appliqué lorsqu'on pense qu'une variable explicative est responsable du problème d'hétéroscédasticité autrement dit l'hypothèse alternative est :
ou f est une fonction de la variable xki, par exemple f(xki) = xki2 .
Dans ce cas on procède de la manière suivante :
1ère étape : trier par ordre croissant des observations en fonction de la variable xk
2ème étape : scinder l’échantillon en 2, en omettant les c observations centrales
3ème étape : estimer la relation avec chaque échantillon composé de N-c/2 observations
4ème étape : tester avec un test de Fisher l’égalité des variances des deux estimations.
Calculer la statistique
Mettre au numérateur la variance estimée la plus élevée. Si la valeur calculée Fcal est plus élevée que la valeur tabulée on refuse l’hypothèse nulle d’homoscédasticité. La puissance du test dépend, en autre, du nombre d'observations c exclues. En pratique, pour un nombre total de 30 observations on peut par exemple omettre 6 observations centrales.
On considère ici le problème d' autocorrélation d'ordre 1 des aléas, on cherche à déterminer dans le cas de données temporelles si et=r et-1+ut avec r un coefficient d’autocorrélation compris entre les valeurs -1 et 1 et u un aléa d’espérance nulle, homoscédastique et non autocorrélé (c’est un bruit blanc). Le test usuel dans le cas d’un modèle statique est le test de Durbin Watson, dans le cas d’un modèle dynamique on applique la statistique h de Durbin. Sous l'hypothèse nulle on a r=0
C Le test de Durbin-Watson (cas d'un modèle statique)
Le test de Durbin Watson utilise les résidus obtenus avec l’estimation du modèle par les MCO. Sous l’hypothèse nulle les aléas ne sont pas autocorrélés d’ordre 1, sous l’hypothèse alternative il y a autocorrélation positive ou négative. La statistique de Durbin Watson s’écrit de la manière suivante :

cette statistique est très proche du coefficient d’autocorrélation de l’échantillon

On montre que la statistique d est approximativement égale à
2(1-![]() ), ainsi une valeur de d proche de 0 signifie une
autocorrélation positive, une valeur proche de 4 une autocorrélation négative et
une valeur proche de 2 la non autocorrélation.
), ainsi une valeur de d proche de 0 signifie une
autocorrélation positive, une valeur proche de 4 une autocorrélation négative et
une valeur proche de 2 la non autocorrélation.
La distribution de la statistique d oscille entre deux distributions dl et du, le règle de décision est la suivante :
0 < d < dl : autocorrélation positive
dl < d < du : zone d’indécision
du < d < 4-du : pas d’autocorrélation
4-du < d < 4 : autocorrélation négative
On peut appliquer ce test notamment lorsque le modèle comporte une constante et lorsque les variables explicatives sont non aléatoires.
Lorsque les aléas sont autocorrélés (dans un modèle statique) on doit appliquer la méthode des MCG. Mais le coefficient d'autocorrélation étant généralement inconnu on doit utiliser des procédures de correction de l'autocorrélation : Cochrane Orcutt, Hildreth-Lu, Prais-Winter,...
C Le test h de Durbin (cas d'un modèle dynamique)
Dans le cas d'un modèle dynamique on doit calculer la statistique h de Durbin :
![]()
avec N le nombre d’observations, d la statistique de Durbin-Watson et
![]() la variance
estimée du coefficient de la variable endogène décalée dans l’estimation du
modèle avec la méthode des MCO. La statistique h est distribuée selon une loi
normale si elle est inférieure à 1,645 (pour un risque de 5%) l’hypothèse nulle
de non autocorrélation est retenue. Si h prend une valeur négative un test
similaire peut-être effectué.
la variance
estimée du coefficient de la variable endogène décalée dans l’estimation du
modèle avec la méthode des MCO. La statistique h est distribuée selon une loi
normale si elle est inférieure à 1,645 (pour un risque de 5%) l’hypothèse nulle
de non autocorrélation est retenue. Si h prend une valeur négative un test
similaire peut-être effectué.
Si ![]() prend une valeur supérieure à 1 on ne peut pas calculer la
statistique h de Durbin. On peut procéder alors de la manière suivante :
prend une valeur supérieure à 1 on ne peut pas calculer la
statistique h de Durbin. On peut procéder alors de la manière suivante :
1. estimer le modèle dynamique avec la méthode des MCO
2. estimer un modèle dont la variable endogène est le vecteur des résidus MCO (e) et les variables explicatives les variables du modèle dynamique (xk k=1,..K et yt-1) et et-1.
3. si le coefficient de la variable et-1 est significativement différent de 0 on peut rejeter l’hypothèse nulle de non autocorrélation.
Lorsque l’hypothèse nulle de non autocorrélation est rejetée il faut estimer le modèle avec la méthode de la variable instrumentale.
Ce test s’applique lorsqu’on veut tester si une variable
explicative comporte une erreur de mesure par rapport
à la variable théorique du modèle économique.
Lorsqu’un problème d’erreur de mesure se présente dans un modèle on doit
appliquer l’estimateur des variables instrumentales (VI) car l’estimateur des
MCO est non convergent.
Sous l’hypothèse nulle (pas d’erreur de mesure) les estimateurs MCO et VI sont
convergents mais l’estimateur des MCO est efficace tandis que l’estimateur des
VI est non efficace. Sous l’hypothèse alternative l’estimateur des MCO est non
convergent tandis que l’estimateur des VI est convergent. Hausman suggère de
calculer la statistique de Wald suivante :

où VVI
et VMCO sont les matrices de variance-covariance estimées des
paramètres estimés, d’une part, avec la méthode des MCO
![]() et d’autre part, avec la méthode des VI
et d’autre part, avec la méthode des VI
![]() . Si la statistique de Wald calculée est inférieure à sa
valeur tabulée on accepte l’hypothèse nulle et on applique la méthode des MCO.
Sinon, on applique l’estimateur des VI.
. Si la statistique de Wald calculée est inférieure à sa
valeur tabulée on accepte l’hypothèse nulle et on applique la méthode des MCO.
Sinon, on applique l’estimateur des VI.
Dans le cas d’un modèle de régression simple, on montre que le test précédent est équivalent à un test de significativité du coefficient de la série des résidus (e) dans le modèle augmenté :
![]()
où u est l’aléa de l’équation augmentée.
- Test d'exogénéité de Spencer et Beck
APPLICATIONS
:
Simulation d'un modèle macroéconomique en
économie fermée
Le modèle de Klein
(modèle macroéconomique dynamique)
Dans
un modèle à plusieurs équations on peut s’interroger sur l’exogénéité d’une
variable explicative notée x* dans une équation.
Soient ![]() l’estimateur des doubles moindres carrés des paramètres de
l’équation qui suppose que la variable x* est exogène et
l’estimateur des doubles moindres carrés des paramètres de
l’équation qui suppose que la variable x* est exogène et ![]() l’estimateur des VI des paramètres de l’équation qui suppose
que la variable x* est endogène.
l’estimateur des VI des paramètres de l’équation qui suppose
que la variable x* est endogène.
Sous l’hypothèse nulle d’exogénéité, les deux estimateurs sont convergents mais
l’estimateur des DMC est efficace. Sous l’hypothèse alternative seul
l’estimateur des VI est convergent. Le test de Spencer de Berk (version du test
d’Hausman adapté à une équation d’un modèle à équations simultanées) consiste à
calculer la statistique de Wald suivante :
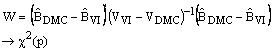
où VVI
et VDMC sont les matrices de variance-covariance estimées des
paramètres estimés, d’une part, avec la méthode des DMC
![]() et d’autre part, avec la méthode des VI
et d’autre part, avec la méthode des VI
![]() . Si la statistique de Wald calculée est inférieure à sa
valeur tabulée on accepte l’hypothèse nulle et on applique la méthode des DMC.
Sinon, on applique l’estimateur des VI. Le degré de liberté du test (p)
correspond au nombre de variables dont on teste l’exogénéité dans l’équation du
modèle. (La version d’Hausman du test utilise l’estimateur des DMC et des TMC).
. Si la statistique de Wald calculée est inférieure à sa
valeur tabulée on accepte l’hypothèse nulle et on applique la méthode des DMC.
Sinon, on applique l’estimateur des VI. Le degré de liberté du test (p)
correspond au nombre de variables dont on teste l’exogénéité dans l’équation du
modèle. (La version d’Hausman du test utilise l’estimateur des DMC et des TMC).
- Test de validité des instruments (test de Sargan)
Ce test se pratique lorsqu'on applique l'estimateur des variables instrumentales, plus précisément lorsque le nombre de d'instrument (p) est supérieur au nombre de variables explicatives. Il s'agit de vérifier la validité des instruments. Soit Z la matrice des instruments, qui comporte un nombre de lignes égal au nombre d'observations et p colonnes, sous l'hypothèse nulle on teste si E(Z' e) = 0 .
Les étapes du test sont les suivantes:
1°) estimer le modèleavec la méthode des variables instrumentales
avec Pz = Z(Z’Z)-1Z’ et calculer la variance
où N correspond au nombre d’observations et ei au résidu de l’estimation précédente.
2°) estimer le modèle de régressionoù
correspond à un vecteur de paramètre de dimension (p,1) et u à un aléa. On note
le vecteur des valeurs prédites du vecteur e.
3°) en déduire la statistique S égale àet distribuée selon une loi du chi deux à p-K degré de liberté.
Si la statistique S est plus faible que la valeur tabulée on ne refuse pas l’hypothèse nulle et on considère que les p instruments sont valides.