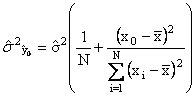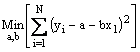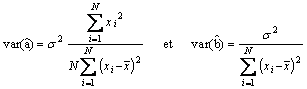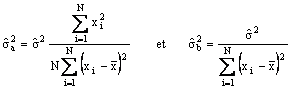Le modèle de régression linéaire simple
- Présentation du modèle
- Méthode d'estimation des Moindres Carrés Ordinaires (MCO)
- Propriétés des estimateurs MCO
- Equation d'analyse de la variance et qualité de l'ajustement
- Inférence statistique
- Prévision
Problème : estimer les paramètres du modèle
yi=a+bxi+ei
avec:
i = 1,...N, N étant le nombre d'observations
yi : la variables expliquée (variable endogène)
xi : la variable explicative (variable exogène)
ei
: un aléa
Hypothèses :
- xi
est supposée non
aléatoire
-
la limite de la variance de
la variable xi est strictement positive
-
ei
est une variable aléatoire
- E(ei)=0
ce qui implique que : E(yi)=a+bxi
-
Var(ei)=s2
, les aléas sont homoscédastiques (la variance est
constante) d'où Var(yi)=s2
-
Cov(ei,ej)=0
avec i différent de j, les aléas ne sont pas autocorrélés d'où Cov(yi,yj)=0
La méthode des MCO consiste à minimiser la somme des carrés des aléas
A partir des conditions du premier ordre on obtient les paramètres estimés :

Les estimateurs des MCO sont BLUE (Best Linear Unbiaised Estimator) et convergents :
C Ils peuvent s'écrire sous la forme d'une combinaison linéaire des observations yi
C Ils sont non biaisé :
C Parmi les estimateurs non biaisés, leur variance est la plus faible (ils sont efficaces)
C L'estimateur des MCO converge en probabilité vers la valeur des paramètres a et b
Sous l'hypothèse de normalité des aléas, les estimateurs des MCO sont des estimateurs du maximum de vraisemblance.
Soit f la fonction de densité de la loi normale, le logarithme de la fonction de vraisemblance s’écrit :
Méthode du maximum de vraisemblance conduit à choisir les estimateurs de a et b tels que la fonction LogL est maximale ou bien tels que la somme des carrés des aléas est minimisée.
La droite de régression de l’échantillon est
donnée par![]() et l’écart entre les valeurs observées et les valeurs
estimées de y est appelé le résidu. La série des résidus (notée e) a une moyenne
nulle et on montre que la variance de y est la somme de la variance de
et l’écart entre les valeurs observées et les valeurs
estimées de y est appelé le résidu. La série des résidus (notée e) a une moyenne
nulle et on montre que la variance de y est la somme de la variance de
![]() et de la variance des résidus :
et de la variance des résidus :
![]()
La qualité de l’ajustement est mesurée par le
coefficient de corrélation (r2 x,y)entre la variable
expliquée et la variable explicative. Il est identique au coefficient de
détermination (R2) donné par le rapport entre la variance de
![]() et la variance de y. Ce coefficient est compris entre 0 et
1. Une valeur proche de 1 indique que la qualité de l’ajustement est bonne.
et la variance de y. Ce coefficient est compris entre 0 et
1. Une valeur proche de 1 indique que la qualité de l’ajustement est bonne.

Un R2 égal à 0,9 signifie que 90% des variations de la variable endogène sont expliquées par le modèle.
Les estimateurs
des MCO sont distribués selon un loi normale.
Cependant, afin d’effectuer des
tests statistiques il faut estimer la variance des aléas. Un estimateur non
biaisé de ![]() est donné par la somme des carrés des résidus divisée par
le nombre d’observations moins le nombre de paramètres estimés :
est donné par la somme des carrés des résidus divisée par
le nombre d’observations moins le nombre de paramètres estimés :
![]()
et la distribution statistique de la
variance estimée des aléas est une loi du Chi-deux :![]()
Ainsi il est possible de calculer la variance estimée des paramètres
et la
distribution des statistiques ![]() est une distribution de Student avec un degré de
liberté égal au nombre d’observations moins le nombre de paramètres estimés
est une distribution de Student avec un degré de
liberté égal au nombre d’observations moins le nombre de paramètres estimés![]() car ces statistiques sont le rapport d'une statistique
distribuée selon une loi normale et d'une statistique dont le carré est
distribué selon une loi du Chi-deux.
car ces statistiques sont le rapport d'une statistique
distribuée selon une loi normale et d'une statistique dont le carré est
distribué selon une loi du Chi-deux.
Le test de significativité des paramètres consiste alors à tester l’hypothèse nulle d’égalité à 0 de chaque paramètre successivement. L’hypothèse est acceptée lorsque la valeur du paramètre estimé rapportée à son écart-type est inférieure en valeur absolue à la statistique de student pour un seuil de risque donné a.
C
Pour donner un
intervalle de confiance de la prévision de la variable y, pour une valeur x0
de x donnée, il faut déterminer l'espérance et la variance de l’erreur de prévision notée e0 ,![]()
L’espérance de l’erreur de prévision est nulle et sa variance est donnée par :

La statistique
![]() est par conséquent distribuée selon une loi normale
d’espérance nulle et de variance égale à celle de l’erreur de prévision. La
variance des aléas étant estimée par
est par conséquent distribuée selon une loi normale
d’espérance nulle et de variance égale à celle de l’erreur de prévision. La
variance des aléas étant estimée par
![]() l’intervalle de confiance de y sachant que la variable x
est égale à x0 s’écrit pour un niveau de risque
a:
l’intervalle de confiance de y sachant que la variable x
est égale à x0 s’écrit pour un niveau de risque
a:
![]()
avec :

C
On peut également donner un
intervalle de confiance de E(y/x=x0). Dans ce cas, la statistique
![]() est distribuée selon une loi normale d’espérance nulle et
de variance
est distribuée selon une loi normale d’espérance nulle et
de variance
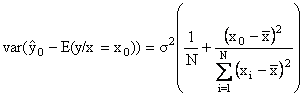
l’intervalle de confiance de E(y/x=x0), pour un niveau de risque a, est donné par :
![]()
avec :