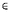
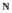 à valeurs dans {0, 1} de la manière suivante : on associe
0 à pile et 1 à face et on dispose de deux pièces de monnaie, une honnête et une truquée qui donne face avec
probabilité 3/4 ;
à valeurs dans {0, 1} de la manière suivante : on associe
0 à pile et 1 à face et on dispose de deux pièces de monnaie, une honnête et une truquée qui donne face avec
probabilité 3/4 ; On génère une suite de variables aléatoires Y = (Y n)n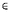
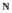 à valeurs dans {0, 1} de la manière suivante : on associe
0 à pile et 1 à face et on dispose de deux pièces de monnaie, une honnête et une truquée qui donne face avec
probabilité 3/4 ;
à valeurs dans {0, 1} de la manière suivante : on associe
0 à pile et 1 à face et on dispose de deux pièces de monnaie, une honnête et une truquée qui donne face avec
probabilité 3/4 ;

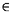 CM(E = {0, 1},
CM(E = {0, 1}, 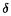 0, N) avec un noyau markovien N défini en termes d’une matrice
stochastique P que vous spécifierez.
0, N) avec un noyau markovien N défini en termes d’une matrice
stochastique P que vous spécifierez.
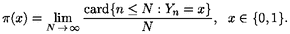
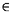 {0, 1}, estimées ci-dessus, calculer
{0, 1}, estimées ci-dessus, calculer 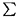 x
x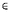 E
E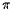 (x)P(x, y).
Qu’observez-vous ?
(x)P(x, y).
Qu’observez-vous ?
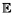 x
x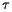 x, pour x
x, pour x 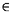 E.
E.
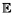 x
x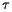 x.
x.
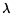 i corresposndantes. Écrire la décomposition spectrale de P.
i corresposndantes. Écrire la décomposition spectrale de P.
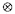 ui et des valeurs propres.
ui et des valeurs propres.
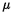 n(x) =
n(x) = 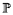 0(Y n = x) pour x = 0, 1.
0(Y n = x) pour x = 0, 1.
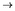
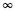
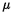 n(x) =
n(x) = 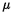
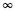 (x) est-elle compatible avec l’observation expérimentale ?
(x) est-elle compatible avec l’observation expérimentale ?
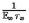 se compare avec
se compare avec 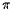 (x) ?
(x) ?L’animation en ligne permet de simuler une chaîne de Markov avec un nombre arbitraire d’états.