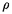 ,
,
Lorsque l’équipement de cette salle de travaux pratiques a été décidé en 1995, les responsables de l’Institut ont envisagé deux options : soit d’équiper la salle d’un gros serveur de calcul et de N terminaux soit de l’équiper d’un petit serveur de fichiers et de N stations indépendantes. Le choix final a reposé sur plusieurs facteurs tels que coût d’acquisition, maintenance, fiabilité, disponibilité, efficacité calculatoire, temps de réponse du serveur, . . . . Afin d’évaluer ce dernier facteur pour l’option d’un gros serveur de calcul, on a procédé à une simulation de la charge du serveur lors d’une séance de travaux pratiques.
Dans la suite de cet exercice, on utilisera une version simplifiée du modèle initialement étudié qui n’intègre pas tous les paramètres qui ont été pris en compte dans l’étude réaliste. Les hypothèses de base de ce modèle simplifié sont que
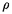 ,
,
On veut estimer la moyenne de la longueur totale des périodes durant lesquelles l’occupation du serveur dépasse un certain seuil de charge s.
Avant de commencer la partie expérimentale de la simulation, il faut lire ce qui suit. Cependant, cette partie de la modélisation peut être traitée de manière théorique, loin des ordinateurs.
Soit (Tk,i )k=1,...,N,i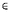
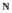 une famille de variables aléatoires indépendantes et identiquement distribuées selon une loi
exponentielle de paramètre
une famille de variables aléatoires indépendantes et identiquement distribuées selon une loi
exponentielle de paramètre 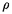 . On note
. On note
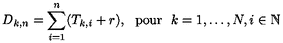
et, pour t 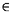 [0,
[0, 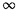 [,
[,
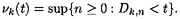
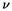 k(D).
k(D).
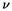 k(D) <
k(D) < 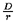 .
.
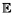 (
(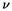 k(D)).
k(D)).
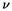 k(D) et
k(D) et 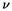 k(D) + 1 sont-elles des temps d’arrêt par rapport à la suite de
tribus (Fk,n)n
k(D) + 1 sont-elles des temps d’arrêt par rapport à la suite de
tribus (Fk,n)n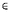
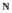 où Fk,n =
où Fk,n = 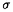 (Tk,1, ..., Tk,n), pour k = 1, ..., N ?
(Tk,1, ..., Tk,n), pour k = 1, ..., N ?
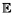 (D
(D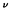 k(D)+1) = (
k(D)+1) = (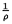 + r)
+ r)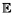 (
(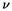 k(D) + 1).
k(D) + 1).
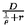 - 1.
- 1.
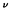 k(t)). Interpréter Ok(t). Dessiner un exemple de trajectoire
typique du processus Ok(t) en fonction de t.
k(t)). Interpréter Ok(t). Dessiner un exemple de trajectoire
typique du processus Ok(t) en fonction de t.
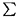 k = 1NOk(t) et
k = 1NOk(t) et
![m = E[c({t (- [0,D] : O(t) > s})],](nte34x.gif)
où 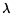 est la mesure de Lebesgue sur [0, D]. Interpéter m.
est la mesure de Lebesgue sur [0, D]. Interpéter m.
On utilisera les données numériques suivantes :
| D (en secondes) | 3600 |
| r (en secondes) | 30 |
| N | 24 |
| s | 8 |
| Nombre | 20 |
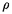 tel que (1 + Nombre)(
tel que (1 + Nombre)(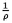 + r) = D.
+ r) = D.
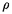 .
.
INTEGER Tab(0:3599) DATA Tab/3600*0/ |