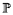 [X < x]. Si FX est
inversible, montrer que FX - 1(U) a même loi que X, où U est une v.a. de loi uniforme sur [0, 1].
[X < x]. Si FX est
inversible, montrer que FX - 1(U) a même loi que X, où U est une v.a. de loi uniforme sur [0, 1].
Application : pour 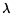 > 0, montrez que Y
> 0, montrez que Y 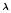 = - 1
= - 1
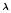 log U est une v.a. de loi exponentielle de paramètre
log U est une v.a. de loi exponentielle de paramètre
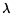 .
.
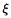 n)n>0 une suite de v.a.i.i.d. positives, indépendantes des v.a. (Xn)n>0, représentant
la demande d’eau pour la période ]n - 1, n]. Le barrage a une capacité totale C et Zn représente le
niveau à la fin de la période ]n - 1, n]. Montrez que
n)n>0 une suite de v.a.i.i.d. positives, indépendantes des v.a. (Xn)n>0, représentant
la demande d’eau pour la période ]n - 1, n]. Le barrage a une capacité totale C et Zn représente le
niveau à la fin de la période ]n - 1, n]. Montrez que
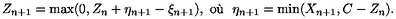
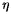 n.
n.
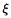 1 est une v.a. de loi exponentielle d’intensité
1 est une v.a. de loi exponentielle d’intensité 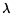 d, et que X1 est une v.a. exponentielle
d’intensité
d, et que X1 est une v.a. exponentielle
d’intensité 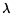 p. Évaluez par simulation l’espérance du nombre de jours de “panne sèche” par an pours
diverses valeurs des paramètres Z0, C,
p. Évaluez par simulation l’espérance du nombre de jours de “panne sèche” par an pours
diverses valeurs des paramètres Z0, C, 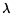 p, et
p, et 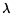 d. Interprétez vos résultats numériques.
d. Interprétez vos résultats numériques.