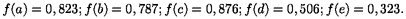4 Problème de Dirichlet discret sur une partie finie du réseau bi-dimensionnel
4.1 Définitions
Soit S = D 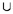 B une partie finie de
B une partie finie de 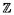 2 telle que :
2 telle que :
- D et B n’ont aucun point en commun et D /= Ø,
- chaque point de D a 4 voisins dans S,
- chaque point de B a au moins un voisin dans D,
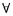 P, Q
P, Q 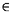 S, il existe une suite de points P1, ..., Pi
S, il existe une suite de points P1, ..., Pi 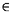 D formant un chemin de P à Q.
D formant un chemin de P à Q.
D est l’ensemble des points intérieurs à S, et B est le bord de S.
Une fonction f définie sur S est dite harmonique si :

Le problème de Dirichlet consiste à déterminer une fonction harmonique sur S, connaissant les valeurs de f sur
le bord B.
4.2 Questions
- Montrer le principe du maximum : une fonction harmonique définie sur S prend sa valeur maximum
et sa valeur minimum sur le bord.
- En déduire le principe d’unicité de Dirichlet : si f et g sont deux fonctions harmoniques sur S
coïncidant sur le bord, alors f = g sur S. (Utiliser le fait que la différence de deux fonctions
harmoniques est une fonction harmonique).
- Nous allons retrouver le principe d’unicité de Dirichlet, par une approche probabiliste, et donner
une expression de la valeur de f sur D, connaissant ses valeurs sur B. Soit (Xn)n>1 une suite de
v.a.i.i.d. à valeurs dans
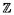 2, telle que
2, telle que
![P[X = (1,0)] = P[X = (- 1,0)] = P[X = (0,-1)] = P[X = (0,1)] = 1.
1 1 1 1 4](nte14x.gif)
Soit x 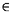 D et (Sn)n>0 la marche aléatoire sur
D et (Sn)n>0 la marche aléatoire sur 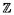 2 définie par
2 définie par
Soit T le temps d’entrée dans B, défini par T = inf{n > 1 : Sn 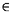 B}, et (SnT)n>0 la marche aléatoire
arrêtée au temps T.
B}, et (SnT)n>0 la marche aléatoire
arrêtée au temps T.
- Soit f harmonique sur S. Montrer que (f(SnT))n>0 est une martingale relativement à la
filtration (
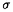 (X0 = x, X1, ..., Xn))n>0.
(X0 = x, X1, ..., Xn))n>0.
- En déduire le principe d’unicité de Dirichlet et montrer que :
![f(x) = Ex[f(ST)],](nte16x.gif)
où 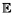 x signifie que la marche aléatoire part de x.
x signifie que la marche aléatoire part de x.
- Utilisez la question précédente pour écrire un algorithme de simulation Monte-Carlo calculant les valeurs
approchées d’une fonction harmonique sur une partie finie S de
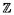 2, connaissant ses valeurs sur le
bord.
2, connaissant ses valeurs sur le
bord.
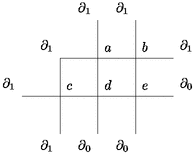
- Testez votre programme sur l’exemple suivant avec D = {a, b, c, d, e} (déterminez une valeur approchée de
f aux points a, b, c, d, e avec des conditions au bord f(
 0) = 0 et f(
0) = 0 et f( 1) = 1.
1) = 1.
- Montrez que le problème discret de Dirichlet sur S
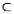
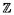 2 peut se résoudre exactement en se ramenant à un
système d’équations linéaires. On pourra résoudre exactement par cette méthode l’exemple proposé , ou
admettre que la solution est :
2 peut se résoudre exactement en se ramenant à un
système d’équations linéaires. On pourra résoudre exactement par cette méthode l’exemple proposé , ou
admettre que la solution est :
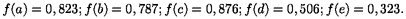
Comparez vos résultats numériques avec les valeurs théoriques.
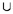 B une partie finie de
B une partie finie de 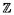 2 telle que :
2 telle que :
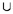 B une partie finie de
B une partie finie de 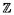 2 telle que :
2 telle que :
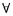 P, Q
P, Q 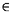 S, il existe une suite de points P1, ..., Pi
S, il existe une suite de points P1, ..., Pi 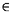 D formant un chemin de P à Q.
D formant un chemin de P à Q.
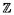 2, telle que
2, telle que
![P[X = (1,0)] = P[X = (- 1,0)] = P[X = (0,-1)] = P[X = (0,1)] = 1.
1 1 1 1 4](nte14x.gif)
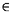 D et (Sn)n>0 la marche aléatoire sur
D et (Sn)n>0 la marche aléatoire sur 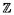 2 définie par
2 définie par 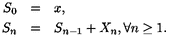
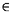 B}, et (SnT)n>0 la marche aléatoire
arrêtée au temps T.
B}, et (SnT)n>0 la marche aléatoire
arrêtée au temps T.
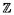 2, connaissant ses valeurs sur le
bord.
2, connaissant ses valeurs sur le
bord.
 0) = 0 et f(
0) = 0 et f( 1) = 1.
1) = 1.
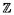 2 peut se résoudre exactement en se ramenant à un
système d’équations linéaires. On pourra résoudre exactement par cette méthode l’exemple proposé , ou
admettre que la solution est :
2 peut se résoudre exactement en se ramenant à un
système d’équations linéaires. On pourra résoudre exactement par cette méthode l’exemple proposé , ou
admettre que la solution est :