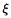 i )i>1 une suite de varianles aléatoires indépendantes et identiquement distribuées selon la loi
uniforme sur {-1, 1}. Soit (Sn)n>0 la suite des somme partielles des variables aléatoires (
i )i>1 une suite de varianles aléatoires indépendantes et identiquement distribuées selon la loi
uniforme sur {-1, 1}. Soit (Sn)n>0 la suite des somme partielles des variables aléatoires (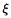 i), à savoir
i), à savoir
Soit (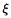 i )i>1 une suite de varianles aléatoires indépendantes et identiquement distribuées selon la loi
uniforme sur {-1, 1}. Soit (Sn)n>0 la suite des somme partielles des variables aléatoires (
i )i>1 une suite de varianles aléatoires indépendantes et identiquement distribuées selon la loi
uniforme sur {-1, 1}. Soit (Sn)n>0 la suite des somme partielles des variables aléatoires (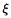 i), à savoir
i), à savoir
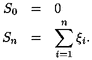
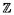 . On introduit le temps aléatoire
T = inf {n > 1 : Sn = 1}. Le but de cet exercice est de déterminer certaines caractéristiques de la loi de
T.
. On introduit le temps aléatoire
T = inf {n > 1 : Sn = 1}. Le but de cet exercice est de déterminer certaines caractéristiques de la loi de
T.
L’animation en ligne permet de visualiser diverses réalisations de la marche aléatoire. Pour une petite valeur de n (commencer avec n = 10) cliquer plusieurs fois sur le bouton de lancement de simulation. Ensuite augmenter la valeur de n à 100 et répéter plusieurs fois. Faire de même avec n = 1000.
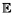 [T] : on calculera la moyenne empirique de
T sur un échantillon obtenue par une boucle réalisant MC réalisations de T. Puisque T peut être très grand,
imposer une limite supérieure MAXT et un compteur d’échecs NBECH de façon que si T n’a pu être
déterminé après MAXT étapes, on incrémente le compteur NBECH d’une unité et on passe à une nouvelle
trajectoire. Pour éviter la recompilation à chaque changement de valeurs, on pourra définir les
paramètres MAXT et MC comme des variables à entrer au clavier. Afficher l’estimation de
[T] : on calculera la moyenne empirique de
T sur un échantillon obtenue par une boucle réalisant MC réalisations de T. Puisque T peut être très grand,
imposer une limite supérieure MAXT et un compteur d’échecs NBECH de façon que si T n’a pu être
déterminé après MAXT étapes, on incrémente le compteur NBECH d’une unité et on passe à une nouvelle
trajectoire. Pour éviter la recompilation à chaque changement de valeurs, on pourra définir les
paramètres MAXT et MC comme des variables à entrer au clavier. Afficher l’estimation de 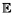 [T] et
NBECH.
[T] et
NBECH.
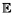 [T] est-il compatible avec la fonction génératrice
[T] est-il compatible avec la fonction génératrice 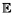 [aT ] = 1-
[aT ] = 1-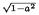 a ?
a ?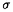 (
(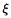 1, ...,
1, ..., 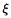 n), montrer que M(
n), montrer que M(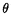 )n =
)n = 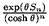 est une martingale et que T
est un temps d’arrêt.
est une martingale et que T
est un temps d’arrêt.
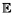 [M(
[M(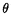 )nT], où M(
)nT], où M(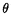 )nT est la martingale arrêtée au temps T.
)nT est la martingale arrêtée au temps T.
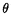 > 0, définir M(
> 0, définir M(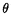 )T = M(
)T = M(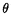 )l sur {T = l} (l = 1, 2, ...), et M(
)l sur {T = l} (l = 1, 2, ...), et M(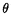 )T = 0 sur {T =
)T = 0 sur {T = 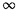 }. Montrer
que lim n
}. Montrer
que lim n 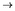
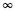 M(
M(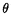 )nT = M(
)nT = M(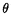 )T .
)T .
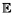 [M(
[M(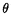 )T ] = 1 pour
)T ] = 1 pour 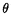 > 0. Utiliser la définition du temps d’arrêt pour établir la
formule concernant la fonction génératrice donnée dans la partie expérimentale (suggestion : poser
a =
> 0. Utiliser la définition du temps d’arrêt pour établir la
formule concernant la fonction génératrice donnée dans la partie expérimentale (suggestion : poser
a = 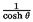 ).
).
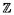 est dite récurrente
nulle).
est dite récurrente
nulle).