Génération de variables aléatoires; principes d’une simulation

1 Génération de variables aléatoires; principes d’une simulation

Écrire le programme FORTRAN suivant :

         SUBROUTINE UNIF ( IX, U )
         INTEGER K1, IX
         REAL U
         K1 = IX / 127773
         IX = 16807 * ( IX - K1 * 127773 ) - K1 * 2836
         IF ( IX .LT. 0 ) IX = IX + 2147483647
         U = IX * 4.656612875e-10
         END
 
         PROGRAM Simulation
         REAL U
         INTEGER IX, I
         WRITE (*,*) ’ Initialisez le generateur’
         READ (*,*) IX
         DO 10 I = 1, 20
         CALL UNIF ( IX, U )
         WRITE (*,*) IX, U
 10      CONTINUE
         END

Sauver ce programme dans un fichier, compilez-le en tapant f77 -u nom-de-fichier et exécutez-le. Essayez différentes valeurs de ix. Qu’observez-vous ? À quoi ressemble la suite des nombres U ainsi obtenue ?

Ce programme est aussi accessible par téléchargement.

Pour vérifier que vous avez programmé correctement, un essai de ce programme peut être effectué en interactif.

Copiez le fichier contenant le programme précédent en un autre fichier et modifiez la partie principale du programme Simulation en :

         PROGRAM Histogramme
         REAL U
         INTEGER I, IX, K, M, HIST (0:9)
         K = 10
         WRITE (*,*) ’ Initialisez le generateur’
         READ (*,*) IX
         DO 10 I = 1, 10000
         CALL UNIF ( IX, U )
         M = K * U
         HIST (M) = HIST (M) +1
 10      CONTINUE
         WRITE (*,*) (HIST (M), M = 0, 9)
         END

Recompilez et re-exécutez le programme. Pouvez-vous formuler une hypothèse en ce qui concerne la nature des nombres U?

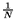
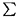Modifier le programme Simulation précédent pour qu’il lise le paramètre entier N et au lieu d’effectuer 20 boucles il en effectue N. Ajouter les commandes qu’il faut pour que S_N = _{i = 1}^NU_i soit calculé et affiché à la fin de la boucle. Faites des essais avec N = 10, 100, 1000. Quelle est votre conclusion ?
Vérifier votre programme à l’aide de l’animation en ligne.
(Principe d’une simulation) Utiliser le premier programme pour générer un suite de variables aléatoires (U_i ) (Il est inutile de stocker cette suite ; il suffit d’utiliser les valeurs au fur et à mesure de leur production) pour calculer la somme $4 sum n 1 Sn = -- ----2- nk=1 1+ Ui$
pour différentes valeurs de n, par exemple, n = 10, 100, 1000, 10000, 100000, 1000000 et comparez le résultat avec 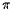. Pour éviter la recompilation à chaque changement de valeurs, on pourra définir le paramètre n comme une variable à entrer au clavier.
Vérifier votre programme à l’aide de l’animation en ligne.
Pouvez-vous montrer que dans un certain sens — à préciser — on a S_n 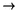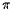? Pouvez-vous proposer une méthode générale de simulation des espérances ?
Soit
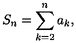
$sum n Sn = ak, k=2$
avec
1. a_k = 1/( log k),
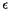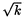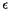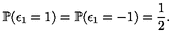
2. a_k = _k/( log k), où (_k) est une suite de variables aléatoires indépendantes et identiquement distribuées selon la loi $P(e1 = 1) = P(e1 = -1) = 1. 2$
Calculer S_n pour n = 10, 100, 1000, 10000, 100000, 1000000 dans les deux cas. Avez-vous une conjecture sur limS_n ? Pouvez-vous justifier cette conjecture ?

[next] [front] [up]