One can hear semitoric systems

---

After several years of work, we can finally claim: yes, one can hear semitoric systems!

What does this mean? Semitoric systems are one of the most simple yet extremely rich family of completely integrable systems with two degrees of freedom. Essentially, they are those who possess a global $S^1$ symmetry. The real definition is a bit more technical: one requires non-degenerate singularities, connectedness of fibers of the ‘energy-momentum’ map, and properness of the Hamiltonian function generating the $S^1$ action.

Now suppose you have a quantum version of these: two commuting operators $(\hat J,\hat H)$ whose underlying classical symbols form a semitoric system $F$ on some symplectic manifold $(M,ω)$. Suppose you “observe” the quantum system like a spectroscopist observing a molecule: you obtain the quantum spectrum; or, more precisely, the joint quantum spectrum of the commuting operators $(\hat J,\hat H)$. From this data, in the semiclassical limit $ħ\to 0$, can you “compute” $(M,ω)$ and $F$?

In this paper¹ with Yohann Le Floch, we prove that the answer is yes, in a strong way: you may extract from the spectrum, in a constructive way, a complete set of symplectic invariants. It remains to apply the classification result obtained with Álvaro Pelayo²'³ to recover $(M,ω)$ and $F$ from these invariants.

---

In the special case of toric systems, the result was previously obtained in this paper⁴ with Laurent Charles and Álvaro Pelayo: from the joint spectrum, one can recover, in the limit $ħ\to 0$, the image of the momentum map, which is a Delzant polytope, and Delzant’s theorem ensures that this is enough to characterize the system.

For more general semitoric systems, there are many more classifying invariants than just the momentum image. In the case of systems “of Jaynes–Cummings type” (semitoric systems with one focus-focus singularity) we previously proved with Álvaro and Yohann the injectivity part: if two such systems have the same joint spectrum, then the classical systems must be isomorphic, see ⁵.

---

The core of our new work¹ is to find explicit formulas for computing all classifying invariants.

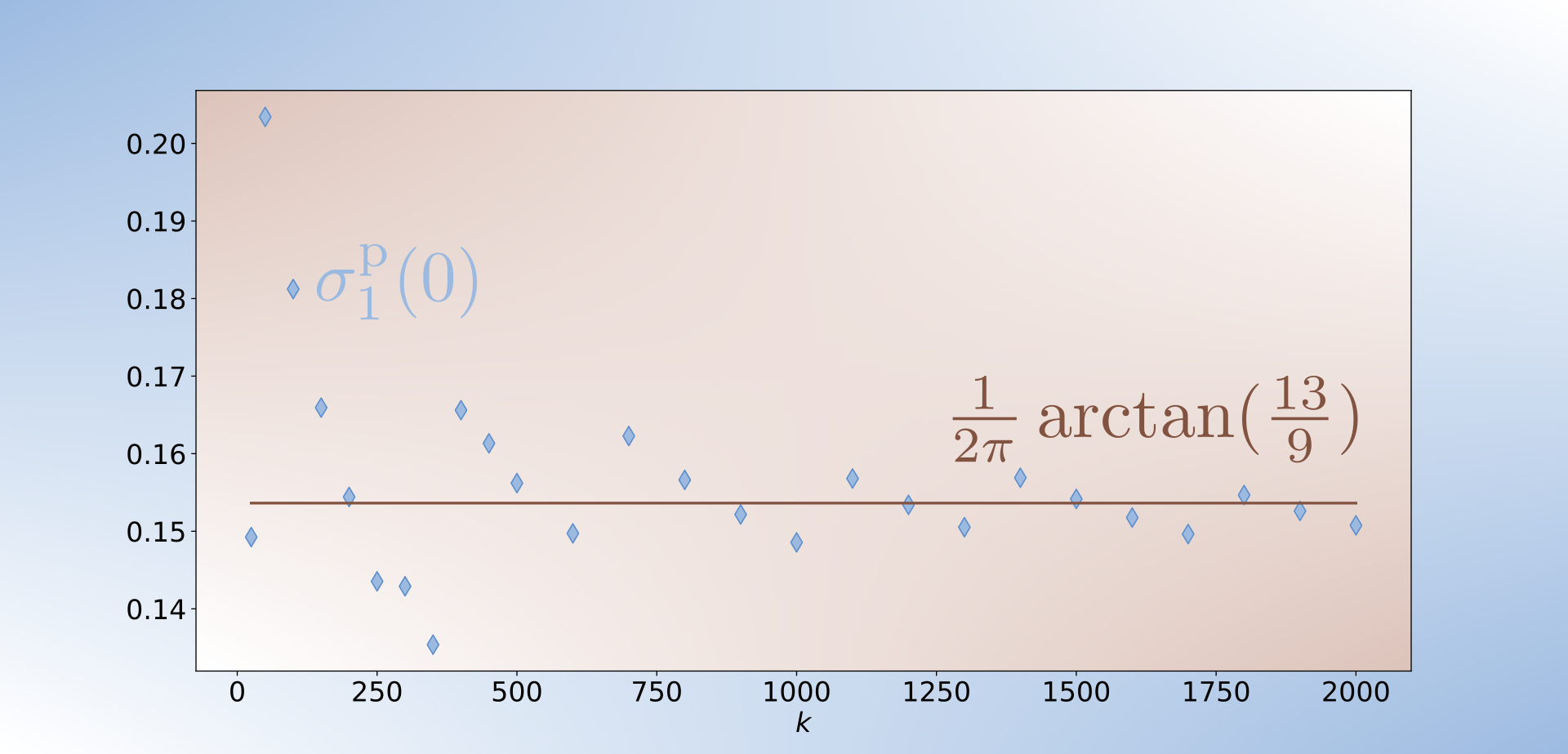
The picture above illustrates how to recover, from the joint spectrum, one of the trickiest invariants: the twisting index combined with one of the linear terms of the Taylor series. The blue diamonds are the quantities obtained from the spectrum, while the brown line is the theoretical value for the particular system under study (spin-orbit coupling on $S^2\times S^2$). Going to the right on this graph corresponds to the semiclassical limit $\hbar\to 0$.

---

It would be very interesting, now, to understand whether and how this inverse spectral problem could fail by relaxing some of the hypothesis in the definition of semitoric systems…

---

1. Y. Le Floch and S. Vũ Ngọc, “The inverse spectral problem for quantum semitoric systems.” Preprint arXiv 2104.06704, April 2021 ↩︎

2. Á. Pelayo and S. Vũ Ngọc, “Constructing integrable systems of semitoric type,” Acta Math., vol. 206, pp. 93–125, 2011. ↩︎

3. Á. Pelayo and S. Vũ Ngọc, “Semitoric integrable systems on symplectic 4-manifolds,” Invent. Math., vol. 177, no. 3, pp. 571–597, 2009. ↩︎

4. L. Charles Á. Pelayo S. Vũ Ngọc, “Isospectrality for Quantum Toric Integrable Systems,” Ann. Sci. École Norm. Sup. 43, pp. 815-849, 2013. ↩︎

5. Y. Le Floch Á. Pelayo S. Vũ Ngọc, “Inverse spectral theory for semiclassical Jaynes-Cummings systems,“ Math. Ann. 364 (3), pp. 1393-1413, 2016. ↩︎