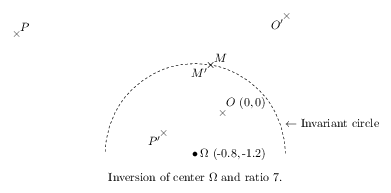
\input fig4tex.tex \figinit{cm} % 1. Characteristic points \figpt 0:$\Omega$ \figcoord{1}(-0.8,-1.2) % Inversion center \def\Rinv{7}\def\sRinv{2.64575} % Inversion ratio and sqrt(ratio) \figpt 1:$O$ \figcoord{0}(0,0) % Origin O \figptinv 11 :$O'$= 1 /0,\Rinv/ % Its image O' by the inversion \figptrot 2 := 11 /0,90/\figpthom 2:$P$=2 /0,1.3/% Compute another point P... \figptinv 12 :$P'$= 2 /0,\Rinv/ % ... and its image P' by the inversion \figptell 21 :$M$: 0;\sRinv,\sRinv (80,0) % Point M lying on the invariant circle... \figptinv 22 :$M'$= 21 /0,\Rinv/ % ... and its image M' by the inversion % 2. Creation of the graphical file \figdrawbegin{} % Draw (half of) the invariant circle \figset (dash=4) \figdrawarccirc 0;\sRinv(0,180) \figdrawend % % 3. Writing text on the figure \figvisu{\figBoxA}{Inversion of center $\Omega$ and ratio \Rinv.}{ % Show the invariant circle \figptell 5 :: 0;\sRinv,\sRinv (20,0) \figwritee 5:$\leftarrow$ Invariant circle(4pt) % Show the involved points \figset write(mark=$\figBullet$)\figwritee 0:(4pt) % Inversion center \figset write(mark=$\times$)\figwritene 1,2,21:(4pt) % Points O, P, M,... \figwritesw 11,12,22:(4pt) % ...and their images O', P', M' by the inversion } \centerline{\box\figBoxA} \bye