 |
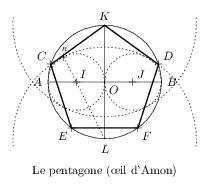
\input fig4tex.tex % construction du pentagone - methode egyptienne connue sous le nom %d'oeil d'Amon - Le cercle de centre K et de rayon LR n'est present %que pour visualiser l'oeil. %Il ne sert pas dans la construction du pentagone %%%%%%%%%%%% % pts caracteristiques %%%%%%%%%%%%% \figinit{2truecm} % % centre et "sommets" du cercle trigonometrique \figpt 1:(0,0) \figpt 2:(0,1) \figpt 3:(1,0) \figpt 4:(-1,0) \figpt 5:(0,-1) % centres des petits cercles interieurs \figptbary 6:[1,4; 1,1] \figptbary 7:[1,3; 1,1] % direction de la droite (LI) \figvectP 8 [5,6] \figvectU 9 [8] % point R : intersection C(I,1/2) et droite (LI) \figpttra 10 := 6 /0.5, 9/ % distance LR = rayon des grands cercles en pointille \figget distance=\Value[10,5] % points C et D : intersection C(O,1) et C(L,LR) \figptsintercirc 11 [1,1 ; 5,\Value] % longueur d'un cote du pentagone \figget distance=\Longueur[2,11] % construction des points E et F pour finir le pentagone \figptsintercirc 13 [1,1 ; 11,\Longueur] \figptsintercirc 16 [1,1 ; 14,\Longueur] %%%%%%%%%%%%%% % fichier graphique %%%%%%%%%%%%%%%% \figdrawbegin{} \figdrawcirc 1 (1) \figdrawline[3,4]\figdrawline[2,5] \figset(dash=5) \figdrawcirc 6(0.5)\figdrawcirc 7(0.5) \figdrawarccirc 5 ; \Value (-5,185) \figdrawarccirc 2 ; \Value (175,365) \figdrawline[5,10] \figreset{general} \figset(width=1) \figdrawline[12,2,11,14,17,12] \figdrawend %%%%%%%%%%%%% % writing %%%%%%%%%%%%% \figvisu{\figBoxA}{Le pentagone (\oe il d'Amon)}{ \figwritese 1:$O$(0.1) \figwriten 2:$K$(0.1) \figwritee 3:$B$(0.1) \figwritew 4:$A$(0.1) \figwrites 5:$L$(0.1) \figset write(mark=+) \figwritene 6:$I$(0.1) \figwritene 7:$J$(0.1) \figwritenw 11:$C$(0.1) \figwritene 12:$D$(0.1) \figwritesw 14:$E$(0.1) \figwritese 17:$F$(0.1) \figwriten 10:$\scriptscriptstyle{R}$(0.1) } \centerline{\box\figBoxA} \bye |