Every data read in the data file is
checked and reported here, along with its meaning. If an error is
encountered during this stage, the execution stops. Three main classes
of error can be found :
- Error during the read instruction. For example, a real data is
given while an integer is expected.
- Error due to an invalid data. For example, a value is out of the
prescribed bounds.
- Error due to a logical conflict between the current data and a
previous one.
These kinds of error may be intermingled.
When an error of the first kind is detected, a message is printed to
the standard output, pointing out the data file record reached when
the error has been found.
For the other kinds of error, a message explaining the problem is
written into this file and also to the standard output.
Once every data has been taken into account, the computation begins. The roots
of the symbol associated to the system of equations and the vectors of
the solution basis are printed whenever the set of elasticity
coefficients changes. Every parameter governing the computation is
printed before the singularities exponents. In the automatic computation
mode, the rectangular domain used to search for the exponents is printed,
and then the exponents found (a rough approximation followed by the
accurate estimation finally kept). Some more information messages may be
printed, mainly concerning the multiplicity and the precision.
If a problem occurs during computation time, a warning or error message
is written into this file and also to the standard output. Such a
message begins with ***, followed by the name of the subroutine
where the problem is detected, and then an explanatory message.
Here are the most common situations leading to a message to be printed:
- The exponent has a ``high" multiplicity and the precision requested
is difficult to obtain. Moreover the
subdivision algorithm may have
reached the limit of the smaller dimension of the rectangular search
domain. The last approximation is then printed, which is generally not
so bad. The user may check this ; he can, for example, restart a
computation with a smaller search domain enclosing the exponent.
- The subdivision algorithm fails. This is a more troublesome
situation since some of, or even all, the exponents may not have been
computed. The best thing to do is to change the initial search domain,
and even to split it in smaller ones if there are too many exponents,
and then start a new computation.
This file contains the values of the angular singular functions
associated to one exponent or several. Some additional informations
are also given in order to make the graphical postprocessing easier.
The structure of the file is organized according to the following
scheme :
 0
(in radians) number K of subdomains
0
(in radians) number K of subdomains
 1
(in radians) number n1 of abscissa evaluated
in the subdomain 1
1
(in radians) number n1 of abscissa evaluated
in the subdomain 1
.
.
 K
(in radians) number nK of abscissa evaluated
in the subdomain K
K
(in radians) number nK of abscissa evaluated
in the subdomain K
Re ( )
Im (
)
Im ( )
)
M
dimension d of the space
SepT Param
Name of the data file (without extension)
n1 values of the function f(1) for subdomain 1
.
.
nK values of the function f(1) for subdomain K
.
.
.
n1 values of the function f(M) for subdomain 1
.
.
nK values of the function f(M) for subdomain K
where
M is the number of singular functions f(i),
i = 1, . . . M associated to  ,
,
SepT is the separation threshold between real and complex exponents,
Param is the value of the parameter governing the computation.
For the subdomain number i, the ni values of the
function are given in ni records (or lines) of the form :
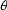 Re (
f1(
Re (
f1(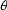 )
)
Im (
f1(
)
)
Im (
f1(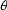 )
)
. . .
Re (
fd(
)
)
. . .
Re (
fd(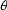 )
)
Im (
fd(
)
)
Im (
fd(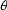 )
)
)
)
where fj is the jth component of the
function, j = 1, . . . d.
This whole block of values is repeated for each exponent found. As this
may lead to a great amount of information, this output is cleary
intended for a small number of exponents.
0 (in radians) number K of subdomains
1 (in radians) number n1 of abscissa evaluated in the subdomain 1
K (in radians) number nK of abscissa evaluated in the subdomain K
) Im (
)
![]() Re (
f1(
Re (
f1(![]() )
)
Im (
f1(
)
)
Im (
f1(![]() )
)
. . .
Re (
fd(
)
)
. . .
Re (
fd(![]() )
)
Im (
fd(
)
)
Im (
fd(![]() )
)
)
)