We now describe the data needed by the program.
*F**** Toute ligne commencant par * est ignoree. . . .
Each item is numbered and must be given in this order. It corresponds to one or several values of a certain type, what we specify using capital letters with the following meaning:
|
|
|||||||||||||||
-
(SI)
Dimension of the space
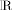 d
: d = 2 or 3.
d
: d = 2 or 3. -
(SI)
Number K of subdomains
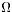 k
composing
k
composing 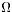 .
.
The maximum number is set to 4, since more complicated arrangements are unusual. Note that this limit may be increased if needed by modifying the settings of the program, detailed in the appendix.
-
(GI)
Code value corresponding to the context of computation.
A code value must be given for each subdomain
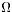 k .
It specifies the characteristics of the material in the subdomain
according to the following convention:
k .
It specifies the characteristics of the material in the subdomain
according to the following convention: -
(GR)
Elasticity coefficients cp q for each subdomain
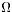 k .
k .
According to the context, the coefficients to give are :
- in dimension 2
- in dimension 3
-
(GR)
Angles (in degrees) defining the geometry of the subdomains.
The angles
 k ,
k = 0,. . . K , are such that
k ,
k = 0,. . . K , are such that
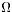 k
lies between
k
lies between
 k-1
and
k-1
and  k .
k .
-
(GI) Boundary conditions.
The two boundaries are defined by the angles
 0 and
0 and
 K .
For each of them, a code corresponding to a boundary condition has to be
given according to the following table:
K .
For each of them, a code corresponding to a boundary condition has to be
given according to the following table:
-
(SI) Action to be performed.
It is given as an integer whose value is 10 a1 + a0 where a0 defines the main action and a1 an optional one. The possible values for a0 are:
- 0 : Manual computation. This is mainly used for tests. The program reads the data until this one ; the following data are not taken into account. Then, it enters in interactive mode. The user has to search for the exponents manually in circular regions of the right part of the complex plane by giving the center and the radius of the circle surrounding this region. First of all, the user has to set the number of points to compute the integrals over this circle ; then he gives the coordinates of the center and the radius. A loop is then executing where the user can change the center and/or the radius, depending on the results obtained. The results consist of the exponent found, its multiplicity and the value of the characteristic determinant.
- 1 : Automatic computation. The exponents are searched in the rectangle defined in the next data item. The program automatically scans this region of the complex plane and prints all the exponents found along with their multiplicity.
- 2 : Automatic computation with rotation of axes.
Available in dimension 3 only.
This action involves the action 1. Moreover, the axes are rotated as if
the point
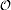 was
moving along a circle according to the settings given below in the
ACTION2 item. The rotation can only be done around the
axis x1 , x2 or x3 .
The geometry of the domains is unchanged during the rotation.
For each position of the point, the computations corresponding to the
action 1 are performed.
was
moving along a circle according to the settings given below in the
ACTION2 item. The rotation can only be done around the
axis x1 , x2 or x3 .
The geometry of the domains is unchanged during the rotation.
For each position of the point, the computations corresponding to the
action 1 are performed.
- 3 :
Automatic computation with variation of the geometry.
This action involves the action 1. Moreover, the position of a boundary
is modified. This boundary may be external (corresponding to
 0
or
0
or  K)
or internal, between two adjacent subdomains. The settings have to be
given below in the ACTION3 item. For each position of the
boundary, the computations corresponding to the action 1 are performed.
K)
or internal, between two adjacent subdomains. The settings have to be
given below in the ACTION3 item. For each position of the
boundary, the computations corresponding to the action 1 are performed.
- 4 : Automatic computation with orientation of the materials. Available in dimension 3 only. This action involves the action 1. Moreover, the fiber direction of each material can be rotated around the axis x1 , x2 or x3 . The settings have to be given below in the ACTION4 item. The geometry of the domains is unchanged during the rotation. For each orientation of the materials, the computations corresponding to the action 1 are performed.
- 5 : Automatic computation with edge tracking.
Available in dimension 3 only.
This action involves the action 1. It is a generalization of the action 2.
The point
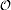 is
supposed to move along an arbitrary smooth curve. This implies that the
axes are rotated and that the geometry of the domains may change.
The settings have to be given below in the ACTION5 item.
For each position of the point, the computations corresponding to the
action 1 are performed.
is
supposed to move along an arbitrary smooth curve. This implies that the
axes are rotated and that the geometry of the domains may change.
The settings have to be given below in the ACTION5 item.
For each position of the point, the computations corresponding to the
action 1 are performed.
Actions with number greater than 1 are devised for computations depending on a parameter which can produce a significant amount of results. For that reason, the optional action is usually used only with actions 0 or 1. The optional action is related to the computation of singular functions. The possible values for a1 are:
- 0 : No optional action.
- 1 : Computation of the kernel of the
characteristic matrix
A(
 ).
).
A basis of the kernel is given along with the corresponding singular value(s) obtained from the SVD decomposition of A( ).
).
- 2 : Computation of the kernel of
A(
 )
and computation of the singular functions and the stress functions.
)
and computation of the singular functions and the stress functions.
This action involves the previous one. Moreover, the angular singular function associated to each exponent is computed and result in two forms:- a text file containing a list of points that can be processed by any graphical software,
- a text file containing a Matlab script that can be executed in the Matlab environment and produces a graph of the fonction.
-
(GR) Rectangular domain where to search for the roots.
This data is necessary when the action number is greater than 0. It consists of the bounds of the domain where the exponents are to be found. The values must be given in the following order: minimum and maximum real part, minimum and maximum imaginary part. The minimum real part must be greater than the threshold Sr.
-
(GC) Keyword related to the action, if its number is
> 1.
This is a character string that must have the form 'ACTIONi ' where i is the value of a0 . Note the space after i. The program looks for this keyword that marks the beginning of the additional data corresponding to the action. Several such keywords may be present in the file: only the data immediately following the keyword corresponding to the selected action is processed.
-
(GIR) Additional data that characterizes the action.
According to the action number, additional data are requested:
- a0 = 2 : The computation point is moving
along a circular curve lying in one of the three main planes, between
the angles
 1 and
1 and
 2 .
The local axes are rotated around one of the absolute axes
xj .
The additional data consist of the definition of the computation points,
that is:
2 .
The local axes are rotated around one of the absolute axes
xj .
The additional data consist of the definition of the computation points,
that is:
- (GR) the 3 angles in degrees: starting angle
 1,
end angle
1,
end angle  2,
step (
2,
step (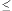
 2 -
2 -
 1),
1),
- (SI) the number j of the rotation axis xj.
- (GR) the 3 angles in degrees: starting angle
- a0 = 3 : The geometry of the domain is
modified through the displacement of a frontier separating two
subdomains, or an external boundary.
The displacement is limited by the position of the two adjacent frontiers.
The additional data consist of the definition of the successive positions
of the frontier, that is:
- (SI) the number k of the concerned frontier
(0
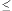 k
k
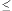 K),
K),
- (GR) the 3 angles in degrees: starting angle
(
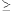
 k-1 ),
end angle (
k-1 ),
end angle ( 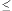
 k+1 ),
step (
k+1 ),
step ( 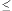
 k+1 -
k+1 -
 k-1 ).
k-1 ).
- (SI) the number k of the concerned frontier
(0
- a0 = 4 : The direction of the fiber of
each material can be rotated around one of the absolute axes
xj. The additional data consist of the definition of
the successive orientations of the materials, that is:
- for each subdomain, one record of the form R R I respectively corresponding to the starting angle, the step (in degrees) and the number j of the rotation axis xj,
- (GI) the number of steps to do and the domain number that defines the abscissa angle on the graphs.
- To fix a material, just take a 0 step ; the rotation axis is without any importance but must be present.
- The number of steps is the same for every material.
- Generally, we want to change the orientation of one material ; the last data is then straightforward. However, when several materials are moving together, one can (and must) choose a "leader" in order to handle the results. This data is not used by the program for the computation ; it is just inserted in the output in order to facilitate the post-processing.
- a0 = 5 : The computation point is moving
along a three dimensional curve, corresponding to an edge of the domain.
At each point, one must know:
- the position of the local axes, which is given by a rotation matrix R . Let B = (x1, x2, x3) the reference basis, in wich the coefficients of the rigidity matrices are given, and B' = (x'1, x'2, x'3) the local basis. The matrix R is defined by R = [ B' ]B , that is Ri j = cos (xi, x'j ).
- the geometry of the subdomains
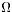 k.
k.
- (SR) the value of the parameter that characterizes the position of the point. It is usually an angle or an arc length. This data is not used by the program for the computation ; it is just inserted in the output in order to facilitate the post-processing.
- (GR) the 9 coefficients of the rotation matrix R given row-wise.
- (GR) the angles
 k ,
k = 0,. . . K , (in degrees) defining
the geometry of the subdomains.
k ,
k = 0,. . . K , (in degrees) defining
the geometry of the subdomains.
- For this action, the data file must end with a data set of the previous form since the program reads the data until it reaches the end of file mark. Nothing else is allowed, except comment lines.
- a0 = 2 : The computation point is moving
along a circular curve lying in one of the three main planes, between
the angles
In the following, the domains are assumed to be numbered counterclockwise.
| Code | Context | Dimension |
|---|---|---|
| 1 | Isotropic elasticity | 2 or 3 |
| 2 | Axisymetric orthotropic elasticity | 2 |
| 3 | Orthotropic elasticity | 2 |
| 4 | General elasticity | 2 or 3 |
An orthotropic material is defined by c16 = c26 = 0. In the axisymetric case, we have moreover c11 = c22 .
| Code 1 : | Lamé
coefficients |
| Code 2 : | coefficients c11 , c12 , c66 |
| Code 3 : | coefficients c11 , c12 , c22 , c66 |
| Code 4 : | coefficients c11 , c12 , c16 , c22 , c26 , c66 |
| Code 1 : | Lamé
coefficients |
| Code 4 : | the 21 coefficients given in the following order |
| c11, | c12 , | . . . | c16 |
| c22 , | . . . | c26 | |
| . | |||
| . | |||
| c66 |
Note that only the order is important, not the structure. For example, the coefficients can be given one per line.
Except a comment line, no separation is allowed between each group of coefficients.
| Code | Type of boundary condition |
|---|---|
| 1 | Dirichlet |
| 2 | Neumann |
| 3 | Mixed normal Dirichlet - tangent Neumann |
| 4 | Mixed tangent Dirichlet - normal Neumann |
| 5 | Transmission |
Note that transmission is allowed only if
![]() K
=
K
=
![]() 0
+ 2
0
+ 2![]() .
.
None of the following items is necessary if the
action number is 0.
None of the following items is necessary if the
action number is 1.