Suivant: il n'y en a pas Précédent:Programmer sous Matlab
Voir: Table des matière - Index - Accueil
![]()
![]()
![]()
Suivant: il n'y en a pas Précédent:Programmer
sous Matlab
Voir: Table des matière
- Index - Accueil
 |
fplot('nomf', [xmin , xmax])
où
Illustrons par des exemples les trois façons d'utiliser la
commande fplot. On obtient le
graphe
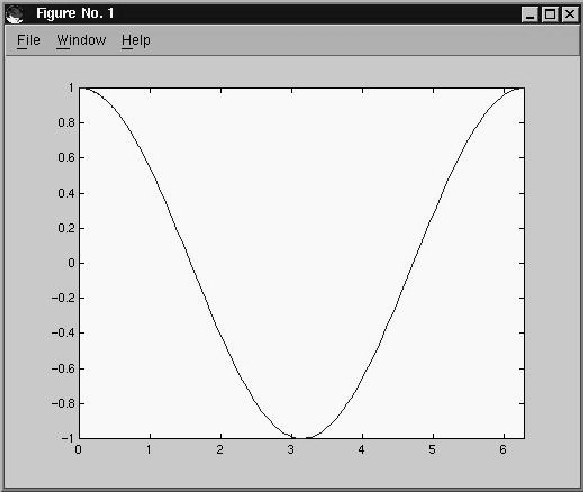
de la fonction incorporée sinus entre ![]() et
et ![]() par l'instruction:
par l'instruction:
fplot('sin',[-2*pi 2*pi]).
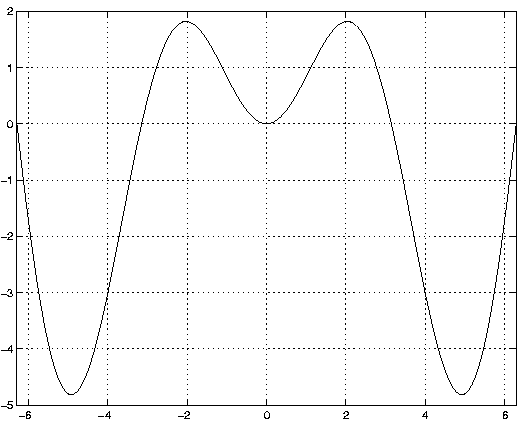
Pour tracer le graphe de la fonction h(x) = x sin(x) entre ![]() et
et ![]() ,
on peut
définir la fonction utilisateur
h dans le fichier h.m
de la manière suivante (attention de bien lire x.*sin(x)
et non pas x*sin(x)):
,
on peut
définir la fonction utilisateur
h dans le fichier h.m
de la manière suivante (attention de bien lire x.*sin(x)
et non pas x*sin(x)):
function y=h(x)On obtient alors le graphe de la fonction h par l'instruction: fplot('h', [-2*pi 2*pi]).
y=x.*sin(x);
 |
Il est possible de tracer plusieurs fonctions sur la même figure. Il faut pour cela utiliser la commande fplot de la manière suivante:
fplot('[nomf_1 , nomf_2 , nomf_3]', [xmin , xmax])
où nomf_1,
nomf_2,
nomf_3
est soit le nom d'une fonction MATLAB
incorporée,
soit une expression définissant une fonction de la variable x,
soit le nom d'une fonction utilisateur.
Il est également possible de gérer les bornes des
valeurs
en ordonnées. Pour limiter le graphe aux ordonnées
comprises
entre les valeurs ymin
et ymax on passera
commesecond
argument de la commande fplot le
tableau [xmin,
xmax, ymin,
ymax].
Une autre possibilité pour gérer les bornes des valeurs
en
ordonnées est d'utiliser la commande axis
après utilisation de la commande fplot.
La syntaxe est axis([xmin,
xmax, ymin,
ymax]).
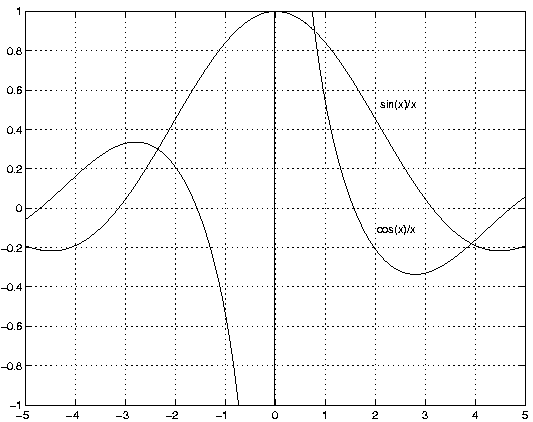
Voici un exemple dont le résultat est affiché à la figure 6:
>> fplot('[sin(x)/x , cos(x)/x]', [-5, 5, -1, 1])
>>
On comprend très vite l'intérêt de gérer les
bornes des valeurs en ordonnées si l'on exécute la
commande
fplot('cos(x)/x',
[-5, 5]) pour tracer le graphe de la fonction cos(x)/x
entre -5 et 5. La figure, qui n'est pas vraiment esthétique,
n'est
pas reproduite ici (-:.
 |
Voici par exemple une autre façon de tracer le graphe de la
fonction
h(x)
= x sin(x) entre ![]() et
et ![]() ,
,
>> x=[-2*pi:0.01:2*pi]; y = x.*sin(x);Essayez aussi
>> plot(x,y)
>>
>> x=[-2*pi:1:2*pi]; y = x.*sin(x);Dans cet exemple on a défini un vecteur x de valeurs équi-réparties entre
>> plot(x,y)
>>
On peut spécifier à MATLAB
quelle
doit être la couleur d'une courbe, quel doit être le style
de trait et/ou quel doit être le symbole à chaque point (xi
, yi). Pour cela on donne un troisième
paramètre
d'entrée à la commande plot
qui est une chaîne de 3 caractères de la forme 'cst'
avec c désignant
la
couleur
du trait,
s le symbole
du point et t le type
de trait. Les possibilités sont les suivantes:
| y | jaune | . | point | - | trait plein |
| m | magenta | o | cercle | : | pointillé court |
| c | cyan | x | marque x | - | pointillé long |
| r | rouge | + | plus | -. | pointillé mixte |
| g | vert | * | étoile | ||
| b | bleu | s | carré | ||
| w | blanc | d | losange | ||
| k | noir | v | triangle (bas) | ||
| ^ | triangle (haut) | ||||
| < | triangle (gauche) | ||||
| > | triangle (droit) | ||||
| p | pentagone | ||||
| h | hexagone |
Les valeurs par défaut sont c = b, s = .
et
t
= - ce qui correspond à un trait plein bleu reliant les
points
entre eux. Il n'est pas obligatoire de spécifier chacun des
trois
caractères. On peut se contenter d'en spécifier un ou
deux.
Les autres seront les valeurs par défaut. La commande grid
permet d'obtenir un quadrillage de la figure, voir par exemple la
figure
6.
Il est possible de tracer plusieurs courbes sur la même figure
en spécifiant plusieurs tableaux x1, y1, x2,
y2,
..., comme paramètres de la commande plot.
Si l'on souhaite que les courbes aient une apparence différente,
on utilisera des options de couleurs et/ou de styles de traits
distincts
après chaque couple de vecteurs x, y.
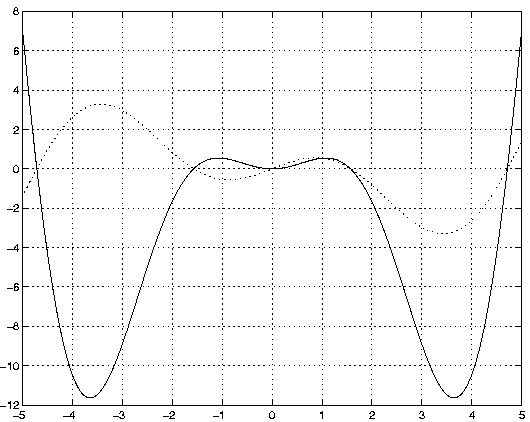
Voici un exemple dont le résultat est affiché à la figure 7. On trace sur l'intervalle [-5, 5] la fonction x² cos(x) en trait plein bleu et la fonction x cos(x) en trait pointillé rouge.
>> x = [-5:0.01:5];
>> y = x.^2.*cos(x); z = x.*cos(x);
>> plot(x,y,'b-',x,z,'r:');
>>
 |
Voici un autre exemple amusant (la commande whitebg permet de passer la fenêtre graphique en inverse vidéo).
>> N=200;
>> x = rand(1,N); y = rand(1,N);
>> plot(x,y,'bd'), whitebg
>>
>> x = [1:10:1000]; y = x.^3;
>> loglog(x,y)
>>
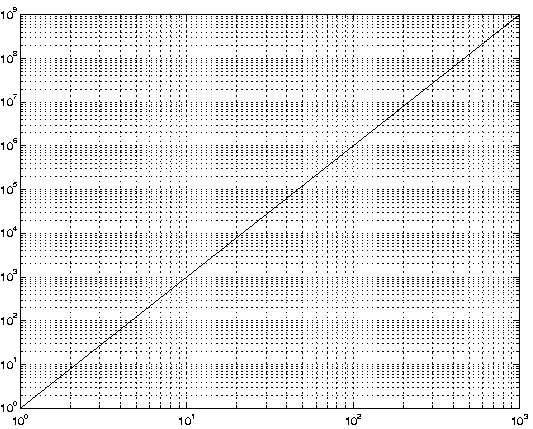 |
xlabel(' légende ')
pour obtenir le mot légende en légende. La commande ylabel fait de même pour l'axe des ordonnées. La commande title permet de donner un titre à la figure. La syntaxe est
title(' le titre')
pour obtenir comme titre le titre.
On peut aussi écrire un texte donné à une position
précise sur la figure grâce à la commande text.
La syntaxe est text(posx,posy,'
un
texte ') où posx
et posy sont les
coordonnées
du point (dans le système associé au dessin) où
doit
débuter l'écriture du texte un
texte. La commande gtext
permet quant à elle de placer le texte à une position
choisie
sur la figure à l'aide de la souris. La syntaxe est gtext('
un
texte '). Une mire, que l'on
déplace
en utilisant la souris, apparaît. Il suffit d'un <<
clic-souris >> pour que le texte
apparaisse à
la position sélectionnée.
Il est possible avec ces commandes d'afficher une valeur contenue dans une variable au milieu de texte. Pour cela on construit un tableau de type chaîne de caractères en convertissant la valeur contenue dans la variable en une chaîne de caractères grâce à la commande num2str. Par exemple, supposons que la variable numex contienne le numéro de l'exemple traité, disons 5. On obtiendra pour titre de la figure Exemple numero 5 par l'instruction: title(['Exemple numero ', num2str(numex)]).
L'exemple suivant dont le résultat est affiché à la figure 9 illustre l'utilisation des différentes commandes permettant de légender une figure.
>> P = 5;
>> t = [0:.01:2];
>> c = 12*exp(-2*t) - 8*exp(-6*t);
>> plot(t,c); grid
>> xlabel('temps en minutes')
>> ylabel('concentation en gramme par litre')
>> title(['evolution de la concentration du produit ', num2str(P), ...
' au cours du temps '])
>> gtext('concentration maximale')
>>
![\includegraphics[scale=0.7]{gr1520.ps}](images/img68.gif) |
>> e = exp(1);
>> figure
>> hold on
>> fplot('exp',[-1 1])
>> fplot('log',[1/e e])
>> plot([-1:0.01:e],[-1:0.01:e])
>> grid
>> hold off
>>
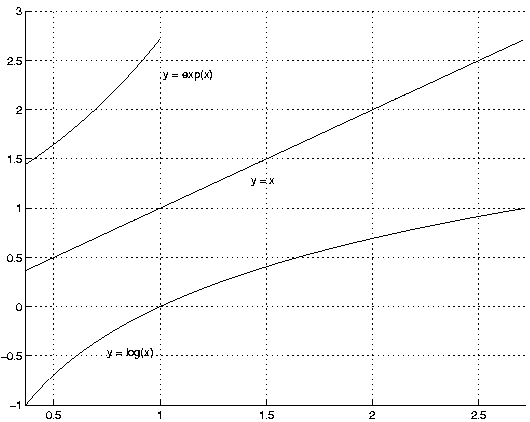 |
On dispose donc de deux façons de superposer plusieurs courbes sur une même figure. On peut soit donner plusieurs couples de vecteurs abscisses/ordonnées comme argument de la commande plot, soit avoir recours à la commande hold on. Suivant le contexte on privilégiera l'une de ces solutions plutôt que l'autre.
Il est possible de décomposer une fenêtre en sous-fenêtres et d'afficher une figure différente sur chacune de ces sous-fenêtres grâce à la commande subplot. La syntaxe est
subplot(m,n,i)
où
>> figure
>> subplot(2,3,1), fplot('cos',[0 4*pi]), title('cosinus'), grid
>> subplot(2,3,2), fplot('sin',[0 4*pi]), title('sinus'), grid
>> subplot(2,3,3), fplot('tan',[-pi/3 pi/3]), title('tangente'), grid
>> subplot(2,3,4), fplot('acos',[-1 1]), title('arc-cosinus'), grid
>> subplot(2,3,5), fplot('asin',[-1 1]), title('arc-sinus'), grid
>> subplot(2,3,6), fplot('atan',[-sqrt(3) sqrt(3)]), title('arc-tangente'), grid
>>
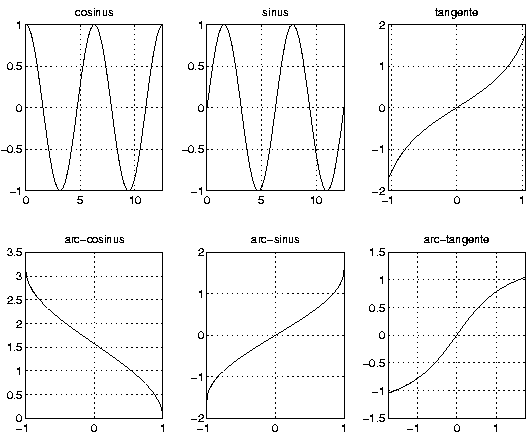 |
print -f<num> -d<format> <nomfic>
où
| ps | : | PostScript noir et blanc |
| psc | : | PostScript couleur |
| eps | : | PostScript Encapsulé noir et blanc |
| epsc | : | PostScript Encapsulé couleur |
| jpeg | : | Format d'image JPEG |
| tiff | : | Format d'image TIFF |
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);On peut également écrire une fonction utilisateur g.m,
>> Z = X.*exp(-X.^2-Y.^2);
>> contour(X,Y,Z)
>>
function x3 = g(x1,x2)et exécuter
x3 = x1.*exp(-x1.^2-x2.^2);
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);Dans les 2 cas on obtient le résultat présenté à la figure 12.
>> Z = g(X,Y);
>> contour(X,Y,Z)
>>
![\includegraphics[scale=0.7]{gr1358.ps}](images/img76.gif) |
Le nombre de lignes de niveau est déterminé de manière automatique à partir des valeurs extrêmes prises par la fonction sur le domaine considéré. Pour imposer le nombre n de lignes de niveau à afficher, il suffit d'appeler la fonction contour avec la valeur n comme quatrième paramètre, contour(X,Y,Z,n).
Il existe deux manières d'afficher les valeurs des lignes de niveau sur la figure. Si l'on souhaite afficher les valeurs pour toutes les lignes de niveau, on utilise la commande clabel de la manière suivante:
>> [C,h] = contour(X,Y,Z,n)Si l'on souhaite afficher uniquement les valeurs de quelques lignes de niveau, on utilise la commande clabel de la manière suivante:
>> clabel(C,h)
>> [C,h] = contour(X,Y,Z,n)On peut alors grâce à la souris sélectionner les lignes de niveau pour lesquelles on souhaite afficher la valeur.
>> clabel(C,h,'manual')
Ainsi pour tracer 30 lignes de niveau de la fonction z = (x -1)2 + 10 (x2 -y)2 sur le domaine [-1 , 1] x [-1 , 1] et pour choisir à l'aide de la souris les lignes de niveau pour lesquelles l'isovaleur doit être affichée, on exécute:
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);Le résultat est présenté à la figure 13.
>> Z = (X-1).^2 + 10*(X.^2-Y).^2;
>> [C,h] = contour(X,Y,Z,30);
>> clabel(C,h,'manual')
>>
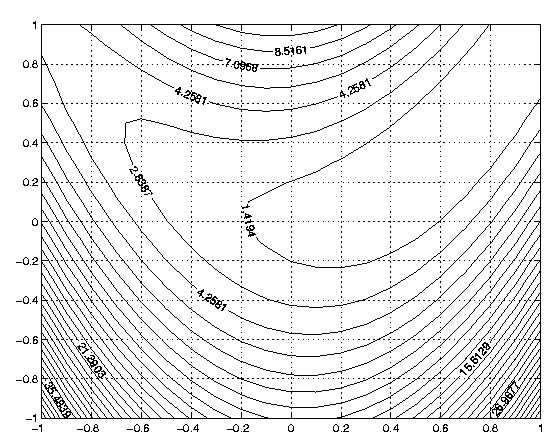 |
Il est possible de modifier la palette des couleurs en utilisant la commande colormap. En tapant help graph3d dans la fenêtre de contrôle MATLAB, vous obtiendrez toutes les palettes de couleurs disponibles. A vous de les tester pour obtenir le meilleur effet (-:. La commande colormap(gray) permet d'utiliser une palette en dégradé de gris, ce qui est très utile si l'on souhaite une impression de la figure sur une imprimante noir et blanc.
La commande contourf s'utilise de la même manière que la commande contour. Elle permet d'afficher, en plus des lignes de niveau, un dégradé continu de couleurs qui varie en fonction des valeurs prises par la fonction. La figure 14 présente un exemple d'utilisation de la commande contourf obtenu de la manière suivante:
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);
>> Z = (X-1).^2 + 10*(X.^2-Y).^2;
>> contourf(X,Y,Z,30);
>> colormap(cool);
>>
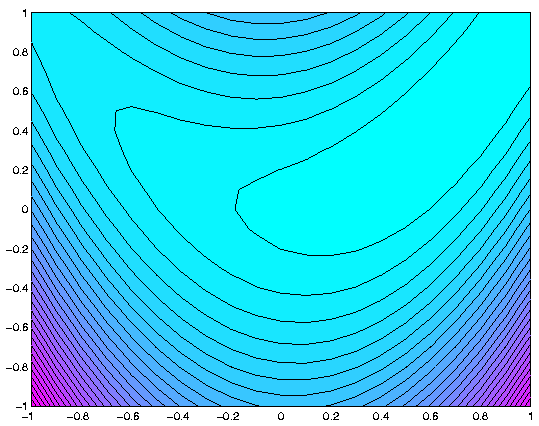 |
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);Si la fonction est définie comme une fonction utilisateur dans le fichier g.m,
>> Z = X.*exp(-X.^2-Y.^2);
>> mesh(X,Y,Z)
>>
function x3 = g(x1,x2)on exécute:
x3 = x1.*exp(-x1.^2-x2.^2);
>> [X,Y] = meshgrid(-2:.2:2, -2:.2:2);Dans les 2 cas on obtient le résultat présenté figure 15.
>> Z = g(X,Y);
>> contour(X,Y,Z)
>>
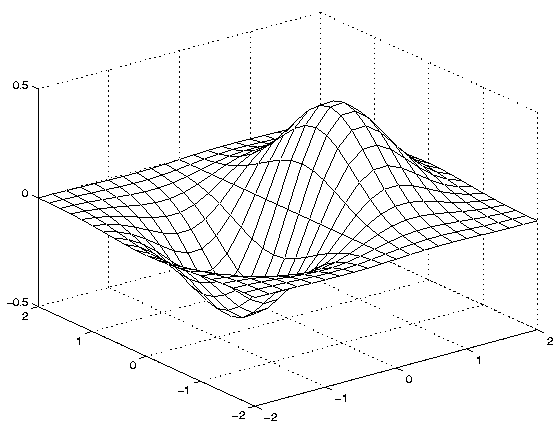 |
Par défaut les valeurs extrêmes en z sont
déterminées
automatiquement à partir des extremums de la fonction sur le
domaine
spécifié. Il est possible de modifier ces valeurs (et
également
les valeurs extrèmes en abscisses et ordonnées) par la
commande
axisdont
la syntaxe est axis(xmin xmax
ymin ymax z_min z_max). Si vous
n'êtes
pas satisfait du résultat, l'instruction axis
auto restaure la figure originale. La figure 16
montre par exemple le résultat de l'instruction axis([
-2 2 -2 2 -2 2]).
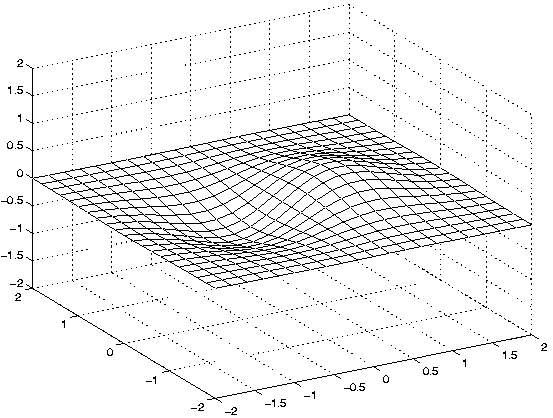 |
I
l est également possible de modifier le point de vision
grâce
à la commande view. La
commande
view a deux arguments qui sont l'angle de vision horizontal et l'angle
de vision vertical en degré. Par défaut ces angles ont
repectivement
les valeurs -37.5o et 30o. La figure
17
montre par exemple le résultat de l'instruction view(37.5,30).
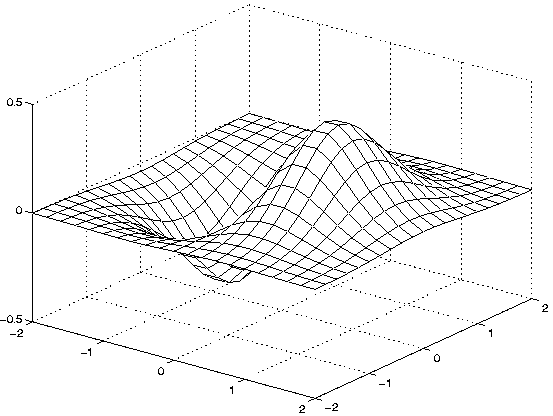 |
Les commandes meshc et
meshz
s'utilisent de la même manière que la commande mesh.
La commande meshc permet
d'afficher
des lignes de niveau sous la surface dans le plan z=zmin.
La commande meshz permet de
tracer
une boite sous la surface. Un exemple d'utilisation de ces commandes
est
présenté à la figure 18.
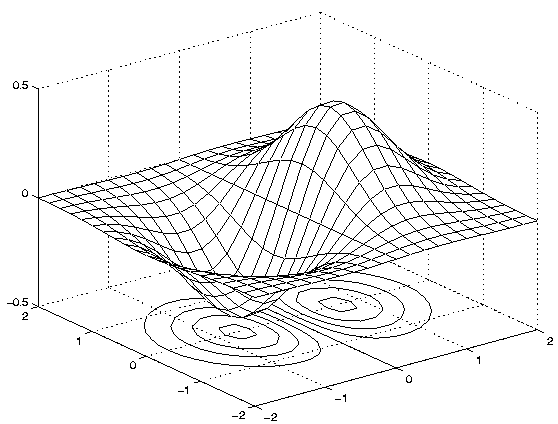
|
La fonction G = (g1, g2,
g3)
peut être définie directement par une expression MATLAB
ou être définie comme une fonction utilisateur. Pour
tracer
la surface paramétrée d'équation (E)
pour umin< u < umax et vmin<
v < vmax on procède de la manière
suivante:
sur le domaine ![]() avec un maillage de maillage de longueur h=0.2, on
exécute:
avec un maillage de maillage de longueur h=0.2, on
exécute:
>> [U,V] = meshgrid(0:.2:2*pi, 0:.2:2);Si la fonction est définie comme une fonction utilisateur dans le fichier G.m,
>> X = V.*cos(U);
>> Y = V.*sin(U);
>> Z = 2*U;
>> surf(X,Y,Z)
function [x1, x2, x3] = G(u,v)on exécute:
x1 = v.*cos(u);
x2 = v.*sin(u);
x3 = 2*u;
>> [U,V] = meshgrid(0:.2:2*pi, 0:.2:2);Dans les 2 cas on obtient le résultat présenté figure 19.
>> [X,Y,Z] = G(U,V);
>> surf(X,Y,Z)
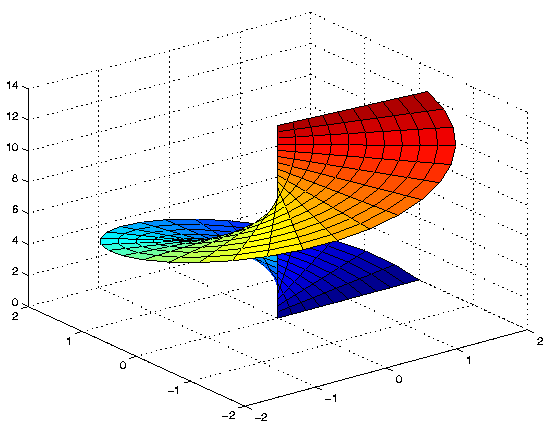 |
 (c)
Stéphane Balac - Centre de Mathématiques - INSA de Lyon
(c)
Stéphane Balac - Centre de Mathématiques - INSA de Lyon