Débuter avec MATLAB

Suivant: Calculer avec MATLAB Précédent:Présentation et généralités
Voir: Table des matière - Index - Accueil

Types de données et variables

Les vecteurs

Les matrices

La structure sparse

Particularités de MATLAB

Comme tout langage de programmation MATLAB permet de définir des données variables. Une variable est désignée par un identificateur qui est formé d'une combinaison de lettres et de chiffres. Le premier caractère de l'identificateur doit nécessairement être une lettre. Attention, MATLAB différencie majuscules et minuscules! Ainsi X33 et x33 désignent deux variables distinctes. Les variables sont définies au fur et à mesure que l'on donne leurs noms (identificateur) et leurs valeurs numériques ou leurs expressions mathématiques. L'utilisation de variables avec MATLAB ne nécessite pas de déclaration de type ou de dimension. Le type et la dimension d'une variable sont déterminés de manière automatique à partir de l'expression mathématique ou de la valeur affectée à la variable. Une variable peut être de type réel, complexe, chaîne de caractères ou logique. Pour MATLAB toute variable est considérée comme étant un tableau d'éléments d'un type donné. MATLAB différencie trois formes particulières de tableaux. Les scalaires qui sont des tableaux à une ligne et une colonne. Les vecteurs qui sont des tableaux à une ligne ou à une colonne. Les matrices qui sont des tableaux ayant plusieurs lignes et colonnes. Une variable MATLAB est donc toujours un tableau que l'on appelle variable scalaire, vecteur ou matrice suivant la forme du tableau.

Les types de données

Les 4 types de données MATLAB

Les trois principaux types de variables utilisés par MATLAB sont les types réel, complexe et chaîne de caractères. Il n'y a pas de type entier à proprement parler. Le type logique est associé au résultat de certaines fonctions. Signalons qu'il est inutile (impossible) de déclarer le type d'une variable. Ce type est établi automatiquement à partir des valeurs affectées à la variable. Par exemple les instructions x = 2; z = 2+i; rep = 'oui'; définissent une variable x de type réel, une variable z de type complexe et une variable rep de type chaîne de caractères.

>> clear
>> x = 2; z = 2+i; rep = 'oui';
>> whos
  Name      Size         Bytes  Class

  rep       1x3              6  char array
  x         1x1              8  double array
  z         1x1             16  double array (complex)

Grand total is 5 elements using 30 bytes
>>

Comme on ne définit pas de manière explicite le type d'une variable, il est parfois utile de pouvoir le déterminer. Cela est possible grâce aux commandes ischar, islogical et isreal. ischar(x) retourne 1 si x est de type chaîne de caractères et 0 sinon. islogical(x) retourne 1 si x est de type logique et 0 sinon. La commande isreal(x) est à utiliser avec discernement: elle retourne 1 si x est réel ou de type chaîne de caractères ((-:) et 0 sinon (x est complexe à partie imaginaire non nulle ou n'est pas un tableau de valeurs réelles ou de caractères).

>> ischar(rep)
ans =
     1
>> ischar(x)
ans =
     0
>> isreal(z)
ans =
     0
>> isreal(x)
ans =
     1
>> isreal(rep)
ans =
     1
>>

Le type complexe

L'unité imaginaire est désignée par i ou j. Les nombres complexes peuvent être écrits sous forme cartésienne a+ib ou sous forme polaire r e^it. Les différentes écritujres possibles sont a+ib, a+i*b, a+b*i, a+bi et r*exp(it) ou r*exp(i*t) avec a, b, r et t des variables de type réel. Les commandes imag, real, abs, angle permettent de passer aisément de la forme polaire à la forme cartésienne et réciproquement. Si z est de type complexe, les instructions im imag(z) et real(z)retournent la partie imaginaire et la partie réelle de z. Les instructions abs(z) et angle(z) retournent le module et l'argument de z. On fera attention au fait que les identificateurs i et j ne sont pas réservés. Aussi il est possible que des variables de noms i et j aient été redéfinies au cours d'un calcul antérieur et soient toujours actives. Si c'est la cas, on peut soit détruire ces deux variables (clear i j), i et j redeviennent alors l'unité imaginaire, soit ré-affecter à i ou à j la valeur unité imaginaire par l'instruction i = sart(-1). On se méfiera donc des boucles d'indices i et j dans lesquelles on manipule des variables de type complexe (-:. On fera également attention à ne pas laisser d'espace autour de l'unité imaginaire afin d'éviter de mauvaises interprétations des données dans certains cas. Comparez par exemple,

>> z = [1+i, 2, 3i]
z =
   1.0000 + 1.0000i   2.0000                  0 + 3.0000i
>> y = [1+i, 2, 3 i]
y =
   1.0000 + 1.0000i   2.0000             3.0000               0 + 1.0000i
>>

Le type chaîne de caractères

Une chaîne de caractères est un tableau de caractères. Une donnée de type chaîne de caractères (char) est représentée sous la forme d'une suite de caractères encadrée d'apostrophes simples ('). Une variable de type chaîne de caractères étant interprétée comme un tableau de caractères, il est possible de manipuler chaque lettre de la chaîne en faisant référence à sa position dans la chaîne. La concaténation de chaînes de caractères s'effectue selon les règles de manipulation des tableaux, voir le paragraphe 2.3. L'exemple suivant présente différentes manipulations d'une chaîne de caractères.

>> ch1 = 'bon'
ch1 =
bon
>> ch2 = 'jour'
ch2 =
jour
>> whos
  Name      Size         Bytes  Class

  ch1       1x3              6  char array
  ch2       1x4              8  char array

Grand total is 7 elements using 14 bytes

>> ch = [ch1,ch2]
ans =
bonjour
>> ch(1), ch(7), ch(1:3)
ans =
b
ans =
r
ans =
bon
>> ch3 = 'soi';
>> ch = [ch(1:3), ch3, ch(7)]
ans = 
bonsoir
>>

Si une chaîne de caractères doit contenir le caractère apostrophe (') celui-ci doit être doublé dans la chaîne (ainsi pour affecter le caractère apostrophe (') à une variable on devra écrire '''', soit 4 apostrophes (-:).

>> rep = 'aujourd'hui'
??? rep = 'aujourd'hui
                   |
Missing operator, comma, or semi-colon.

>>  rep = 'aujourd''hui'
rep =
aujourd'hui
>>  apos = ''''
apos =
'
>>

La chaîne de caractères vide s'obtient par 2 apostrophes ''. La commande isempty permet de tester si une variables de type chaîne de caractères est vide ou non. La commande strcmp permet de tester si deux chaines de caractères sont égales ou non.

Le type logique

Le type logique (logical) possède 2 formes: 0 pour faux et 1 pour vrai. Un résultat de type logique est retourné par certaines fonctions ou dans le cas de certains tests. Dans l'exemple qui suit on considère une variable x contenant la valeur 123 et une variable y définie par l'expression mathématique y = exp(log(x)). On teste si les variables x et y contiennent les mêmes valeurs. La variable tst est une variable de type logique qui vaut 1 (vrai) les valeurs sont égales et 0 (faux) sinon. Suivant la valeur de tst, on affiche la phrase x est egal a y ou la phrase x est different de y. Dans l'exemple proposé, compte-tenu des erreurs d'arrondis lors du calcul de exp(log(123)), la valeur de la variable y ne vaut pas exactement 123. On pourra également considérer le cas où x=12.

>> x = 123; y = exp(log(x));
>> tst = ( x==y );
>> if tst, disp('x est egal a y '), else disp('x est different de y '), end
x est different de y
>> whos
  Name      Size         Bytes  Class

  tst       1x1              8  double array (logical)
  x         1x1              8  double array
  y         1x1              8  double array

Grand total is 3 elements using 24 bytes

>> format long
>> x, y, tst
x =
   123
y =
     1.229999999999999e+02
tst =
     0
>> format, clear
>>

Les vecteurs

Définir un vecteur

On définit un vecteur ligne en donnant la liste de ses éléments entre crochets ([ ]). Les éléments sont séparés au choix par des espaces ou par des virgules. On définit un vecteur colonne en donnant la liste de ses éléments séparés au choix par des points virgules (;) ou par des retours chariots (touche Entrée/Enter). On peut transformer un vecteur ligne x en un vecteur colonne et réciproquement en tapant x' (' est le symbole de transposition). Il est inutile de définir la longueur d'un vecteur au préalable. Cette longueur sera établie automatiquement à partir de l'expression mathématique définissant le vecteur ou à partir des données. On peut obtenir la longueur d'un vecteur donné grâce à la commande length. Un vecteur peut également être défini << par blocs >> selon la même syntaxe. Si par exemple x₁, x₂ et x₃ sont trois vecteurs (on note x1, x2 et x3 les variables MATLAB correspondantes), on définit le vecteur bloc (x₁ | x₂ | x₃ ) par l'instruction X = [x1 x2 x3].

>> x1 = [1 2 3], x2 = [4,5,6,7], x3 = [8; 9; 10]
x1 =
     1     2     3
x2 =
     4     5     6     7
x3 =
     8
     9
    10
>> length(x2), length(x3)
ans =
     4
ans =
     3
>> whos
  Name      Size         Bytes  Class

  x1        1x3             24  double array
  x2        1x4             32  double array
  x3        3x1             24  double array

Grand total is 10 elements using 80 bytes

>> x3'
ans =
     8     9    10
>> X = [x1 x2 x3']
X =
     1     2     3     4     5     6     7     8     9    10
>>

Les éléments d'un vecteur peuvent être manipulés grâce à leur indice dans le tableau. Le k-ieme élément du vecteur x est désignée par x(k). Le premier élément d'un vecteur a obligatoirement pour indice 1. En pratique ceci impose de faire des translations d'indices si par exemple on souhaite définir une suite (x₀ , x₁ , ... , x_n). Le terme x₀ de la suite correspondra à l'élément x(1) du vecteur et le terme x_N à l'élément x(N+1). Il est possible de manipuler plusieurs éléments d'un vecteur simultanément. Ainsi les éléments k à l du vecteur x sont désignés par x(k:l). On peut également manipuler facilement les éléments d'un vecteur dont les indices sont en progression arithmétique. Ainsi si l'on souhaite extraire les éléments k, k+p, k+2p,..., k+Np = l, on écrira x(k:p:l). Plus généralement, si K est un vecteur de valeurs entières, X(K) retourne les éléments du vecteur X dont les indices sont les éléments du vecteur K. Reprenons l'exemple précédent.

>> X(5)
ans =
     5
>> X(4:10)
ans =
     4     5     6     7     8     9    10
>> X(2:2:10)
ans =
     2     4     6     8    10
>> K = [1 3 4 6]; X(K)
ans =
     1     3     4     6 
>>

Il est très facile de définir un vecteur dont les composantes forment une suite arithmétique. Pour définir un vecteur x dont les composantes forment une suite arithmétique de raison h, de premier terme a et de dernier terme b, on écrira x = a:h:b. Si a-b n'est pas un multiple de h, le dernier élément du vecteur x sera a + Ent((a-b)/h) h où Ent est la fonction partie entière. La commande linspace permet de définir un vecteur x de longueur N dont les composantes forment une suite arithmétique de premier terme a et de dernier terme b (donc de raison (a-b)/N). Les composantes du vecteur sont donc linéairement espacés. La syntaxe est x = linspace(a,b,N).

>> x = 1.1:0.1:1.9
x =
  Columns 1 through 7 
    1.1000    1.2000    1.3000    1.4000    1.5000    1.6000    1.7000
  Columns 8 through 9 
    1.8000    1.9000
>> x = 1.1:0.2:2
x =
    1.1000    1.3000    1.5000    1.7000    1.9000
>> x = linspace(1.1,1.9,9)
ans =
  Columns 1 through 7 
    1.1000    1.2000    1.3000    1.4000    1.5000    1.6000    1.7000
  Columns 8 through 9 
    1.8000    1.9000
>>

Vecteurs spéciaux

Les commandes ones, zeros et rand permettent de définir des vecteurs dont les éléments ont respectivement pour valeurs 0, 1 et des nombres générés de manière aléatoire.

ones(1,n)	:	vecteur ligne de longueur n dont tous les éléments valent 1
ones(m,1)	:	vecteur colonne de longueur m dont tous les éléments valent 1
zeros(1,n)	:	vecteur ligne de longueur n dont tous les éléments valent 0
`zeros(m,1)`	:	vecteur colonne de longueur m dont tous les éléments valent 0
`rand(1,n)`	:	vecteur ligne de longueur n dont les éléments sont générés de manière aléatoire entre 0 et 1
`rand(m,1)`	:	vecteur colonne de longueur m dont les éléments sont générés de manière aléatoire entre 0 et 1

Les matrices

Définir une matrice

On a déjà vu que l'on définissait la matrice

en tapant A = [ 1 3; 4 2 ]. D'une façon générale, on définit une matrice en donnant la liste de ses éléments entre crochets. Signalons que MATLAB admet d'autres façons d'écrire les matrices. Les éléments d'une ligne de la matrice peuvent être séparés au choix par un blanc ou bien par une virgule (,). Les lignes quant à elles peuvent être séparées au choix par le point-virgule (;) ou par un retour chariot. Par exemple, on peut aussi écrire la matrice A de la manière suivante,

>> A = [1,3;4,2]
A =
     1     3
     4     2

>> A = [1 3
        4 2]
A =
     1     3
     4     2
>> A = [1,3
        4,2]
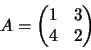
A =
     1     3
     4     2
>>

Un élément d'une matrice est référencé par ses numéros de ligne et de colonne. A(i,j) désigne le i-ième élément de la j-ièmeligne ligne de la matrice A. Ainsi A(2,1) désigne le premier élément de la deuxième ligne de A,

>> A(2,1)
ans =
      4
>>

La commande size permet d'obtenir les dimensions d'une matrice A donnée. On peut soit obtenir de manière séparée le nombre de lignes et de colonnes par les instructions size(A,1)et size(A,2)respectivement, soit obtenir le nombre m de lignes et le nombre n de colonnes par l'instruction [m,n] = size(A).

On peut construire très simplement une matrice << par blocs >> . Si A, B, C, D désignent 4 matrices (aux dimensions compatibles), on définit la matrice bloc,

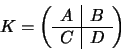
par l'instruction K = [A B ; C D]. Voici un exemple de construction par blocs de la matrice

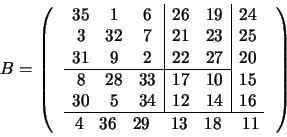
$\begin{displaymath}B = \left(\begin{array}{c}\begin{array}{c c c \vert c c \......& 18 & \phantom{\vert} 11\\\end{array}\end{array}\right)\end{displaymath}$

>> A11 = [35 1 6; 3 32 7; 31 9 2];
>> A12 = [26 19; 21 23; 22 27];
>> A21 = [ 8 28 33; 30 5 34];
>> A22 = [17 10; 12 14];
>> B11 = [ A11 A12; A21 A22 ]
B11 =
    35     1     6    26    19
     3    32     7    21    23
    31     9     2    22    27
     8    28    33    17    10
    30     5    34    12    14
>> B12 = [ 24 25 20 15 16]';
>> B = [ B11 B12];
>> B21 = [ 4 36 29 13 18 11];
>> B = [ B ; B21]
B =
    35     1     6    26    19    24
     3    32     7    21    23    25
    31     9     2    22    27    20
     8    28    33    17    10    15
    30     5    34    12    14    16
     4    36    29    13    18    11
>>

Matrices spéciales

Certaines matrices se construisent très simplement grâce à des commandes dédiées. Citons les plus utilisées:

`eye(n)`	:	la matrice identité de dimension n
`ones(m,n)`	:	la matrice à `m` lignes et `n` colonnes dont tous les éléments valent 1
`zeros(m,n)`	:	la matrice à `m` lignes et `n` colonnes dont tous les éléments valent 0
`rand(m,n)`	:	une matrice à `m` lignes et `n` colonnes dont les éléments sont générés de manière aléatoire entre 0 et 1

Signalons que si les entiers m et n sont égaux on peut se contenter de ne spécifier qu'une seule valeur de dimension: ones(n) est la matrice carrée de dimension n dont tous les éléments valent 1. Mentionnons enfin la commande magic(n) qui permet d'obtenir une matrice magique de dimension n.

>> eye(3)
ans =
     1     0     0
     0     1     0
     0     0     1
>> ones(3,2)
ans =
     1     1
     1     1
     1     1
>> zeros(2)
ans =
     0     0
     0     0
>> rand(2,3)
ans =
    0.4565    0.8214    0.6154
    0.0185    0.4447    0.7919
>> magic(6)
ans =
    35     1     6    26    19    24
     3    32     7    21    23    25
    31     9     2    22    27    20
     8    28    33    17    10    15
    30     5    34    12    14    16
     4    36    29    13    18    11
>>

Manipuler des matrices

Le symbole deux-points (:) permet d'extraire simplement des lignes ou des colonnes d'une matrice. Le j-ieme vecteur colonne de la matrice A est désigné par A(:,j). C'est simple, il suffit de traduire le symbole deux-points (:) par << tout >>. Ainsi A(:,j) désigne toutes les lignes et la j-ieme colonne de la matrice A. Bien entendu, la i-ieme ligne de la matrice A est désignée par A(i,:).

>> A = magic(5)
A =
    17    24     1     8    15
    23     5     7    14    16
     4     6    13    20    22
    10    12    19    21     3
    11    18    25     2     9
>>  A(1,:)
ans =
    17    24     1     8    15
>>  A(:,2)
ans =
    24
     5
     6
    12
    18
>>

Si l'on souhaite échanger les colonnes 2 et 3 de la matrice A une première possibilité consiste à exécuter:

>> v = A(:,2); A(:,2) = A(:,3); A(:,3) = v;
A =
    17     1    24     8    15
    23     7     5    14    16
     4    13     6    20    22
    10    19    12    21     3
    11    25    18     2     9
>>

On peut également extraire plusieurs lignes ou colonnes simultanément. Si J est un vecteur d'entiers, A(:,J)est la matrice issue de A dont les colonnes sont les colonnes de la matrice A d'indices contenus dans le vecteur J. De même A(J,:)est la matrice issue de A dont les lignes sont les lignes de la matrice A d'indices contenus dans le vecteur J. D'une façon plus générale, il est possible de n'extraire qu'une partie des éléments des lignes et colonnes d'une matrice. Si L et C sont deux vecteurs d'indices, A(L,C)désigne la matrice issue de la matrice A dont les éléments sont les A(i,j) tels que i soit dans L et j soit dans C.

>> A = magic(5)
A =
    17    24     1     8    15
    23     5     7    14    16
     4     6    13    20    22
    10    12    19    21     3
    11    18    25     2     9
>> L = [1 3 5]; C = [3 4];
>> A(L,C)
ans =
     1     8
    13    20
    25     2
>> A(1:2:5,3:4)
ans =
     1     8
    13    20
    25     2
>>

Dans la dernière instruction, on a utilisé la forme spéciale permettant de définir un vecteur dont les composantes sont en progression arithmétique, voir le paragraphe 2.3. Une seconde possibilité pour échanger les lignes 2 et 3 de la matrice A consiste à exécuter:

>> J = [1 3 2 4]; A = A(:,J)
A =
    17     1    24     8    15
    23     7     5    14    16
     4    13     6    20    22
    10    19    12    21     3
    11    25    18     2     9
>>

Il existe des commandes MATLAB permettant de manipuler globalement des matrices. La commande diag permet d'extraire la diagonale d'une matrice: si A est une matrice, v=diag(A) est le vecteur composé des éléments diagonaux de A. Elle permet aussi de créer une matrice de diagonale fixée: si v est un vecteur de dimension n, A=diag(v) est la matrice diagonale dont la diagonale est v.

>> A=eye(3); diag(A)
ans =
     1
     1
     1
>> v=[1:3]
v =
     1 2 3
>> diag(v)
 ans =
     1 0 0
     0 2 0
     0 0 3
>>

On n'est pas obligé de se limiter à la diagonale principale ... La commande diagadmet un second paramètre k pour désigner la k sur-diagonale (si k>0) ou la k sous-diagonale (si k<0).

>> A = [4 5 6 7 ; 3 4 5 6
        2 3 4 5; 1 2 3 4]
A =
     4     5     6     7
     3     4     5     6
     2     3     4     5
     1     2     3     4
>> diag(A,1)
ans =
     5
     5
     5
>> diag(A,-2)
ans =
     2
     2
>>

On construit à l'aide de la commande diagtrès simplement des matrices tridiagonales . Par exemple la matrice correspondant à la discrétisation par différences finies du problème de Dirichlet en dimension 1 s'obtient ainsi

>> N=5;
>> A=diag(2*ones(N,1)) - diag(ones(N-1,1),1) - diag(ones(N-1,1),-1)
A =
     2    -1     0     0     0
    -1     2    -1     0     0
     0    -1     2    -1     0
     0     0    -1     2    -1
     0     0     0    -1     2
>>

On dispose également de la commande tril permet d'obtenir la partie triangulaire inférieure (l pour lower) d'une matrice. La commande triupermet d'obtenir la partie triangulaire supérieure (u pour upper) d'une matrice.

>> A = [ 2 1 1 ; -1 2 1 ; -1 -1 2]
A =
     2     1     1
    -1     2     1
    -1    -1     2
>> triu(A)
ans =
     2     1     1
     0     2     1
     0     0     2
>> tril(A)
ans =
     2     0     0
    -1     2     0
    -1    -1     2
>>

Comme pour la commande diag, les commandes triu et triladmettent un second paramètre k. On peut ainsi obtenir la partie triangulaire supérieure (ou inférieure) à partir de la k diagonale. Ainsi,

>> tril(A,-1)
ans =
     0     0     0
    -1     0     0
    -1    -1     0
>> tril(A,1)
ans =
     2     1     0
    -1     2     1
    -1    -1     2
>>

On obtient la transposée de la matrice Aà coefficients réels en tapant A'. Si la matrice est à coefficients complexes, A'retourne la matrice adjointe de A.

>> A = [0 1 2; -1 0 1; -2 -1 0]
A =
     0     1     2
    -1     0     1
    -2    -1     0
>> A'
ans =
     0    -1    -2
     1     0    -1
     2     1     0
>>

La structure sparse

On appelle matrice creuse (le terme anglais est sparse matrix ) une matrice comportant une forte proportion de coefficients nuls. De nombreux problèmes issus de la physique conduisent à l'analyse de systèmes linéaires à matrice creuse. L'intérêt de telles matrices résulte non seulement de la réduction de la place mémoire (on ne stocke pas les zéros) mais aussi de la réduction du nombre d'opérations (on n'effectuera pas les opérations portant sur les zéros). Par défaut dans MATLAB une matrice est considérée comme pleine (ou full en anglais), c'est-à-dire que tous ses coefficients sont mémorisés. Si M est une matrice, la commande sparse(M) permet d'obtenir la même matrice mais stockée sous la forme sparse. Si l'on a une matrice stockée sous la forme sparse, on peut obtenir la même matrice stockée sous la forme ordinaire par la commande full. Il est possible de visualiser graphiquement la structure d'une matrice grâce à la commandespy. Si M est une matrice, la commandespy(M)ouvre une fenêtre graphique et affiche sous forme de croix les éléments non-nuls de la matrice. Le numéro des lignes est porté sur l'axe des ordonnées, celui des colonnes en abscisse. On obtient également le nombre d'éléments non-nuls de la matrice. La commande nnz permet d'obtenir le nombre d'éléments non-nuls d'une matrice. Reprenons l'exemple de la matrice tridiagonale issue de la discrétisation par différences finies du problème de Dirichlet en dimension 1.

>> N=5;
>> A=diag(2*ones(N,1)) - diag(ones(N-1,1),1) - diag(ones(N-1,1),-1)
A =
     2    -1     0     0     0
    -1     2    -1     0     0
     0    -1     2    -1     0
     0     0    -1     2    -1
     0     0     0    -1     2
>> nnz(A)
ans =
    13  
>> B = sparse(A)
B =
   (1,1)        2
   (2,1)       -1
   (1,2)       -1
   (2,2)        2
   (3,2)       -1
   (2,3)       -1
   (3,3)        2
   (4,3)       -1
   (3,4)       -1
   (4,4)        2
   (5,4)       -1
   (4,5)       -1
   (5,5)        2
>> whos
  Name      Size         Bytes  Class

  A         5x5            200  double array
  B         5x5            180  sparse array
  N         1x1              8  double array

Grand total is 39 elements using 388 bytes
>> spy(A)
>>

$\includegraphics[scale=0.5]{spy.ps}$

Figure 2: Résultat de la commandespy(B).

Pour les très grosses matrices creuses, il n'est bien entendu pas souhaitable d'utiliser une structure pleine (full) pour définir la matrice avant de passer en stockage sparse. La commande sparsepermet de définir une matrice creuse directement sous la forme sparse. On l'utilise de la façon suivante: A = sparse(is,js,s,n,m) pour définir une matrice A à n lignes et m colonnes dont les coefficients sont nuls (et donc non mémorisés) sauf les éléments a_is(l),js(l) qui valent s(l) pour l variant de 1 à L longueur du tableau s (L = length(s)).

>> N=5;
>> s =[2*ones(1,N), -ones(1,N-1), -ones(1,N-1)]
s =
  Columns 1 through 12
     2     2     2     2     2    -1    -1    -1    -1    -1    -1    -1
  Column 13
    -1
>> is = [1:N,1:N-1,2:N]
is =
  Columns 1 through 12
     1     2     3     4     5     1     2     3     4     2     3     4
  Column 13
     5
>> js = [1:N,2:N,1:N-1]
js =
  Columns 1 through 12
     1     2     3     4     5     2     3     4     5     1     2     3
  Column 13
     4
>> B = sparse(is,js,s,N,N)
B =
   (1,1)        2
   (2,1)       -1
   (1,2)       -1
   (2,2)        2
   (3,2)       -1
   (2,3)       -1
   (3,3)        2
   (4,3)       -1
   (3,4)       -1
   (4,4)        2
   (5,4)       -1
   (4,5)       -1
   (5,5)        2
>> A = full(B)
A =
     2    -1     0     0     0
    -1     2    -1     0     0
     0    -1     2    -1     0
     0     0    -1     2    -1
     0     0     0    -1     2        
>>

Les commandes spdiags, speyeet sprandpermettent de construire des matrices diagonales, identités et des matrices dont les éléments sont des nombres aléatoires avec un stockage sparse. Elles s'utilisent de la même manière que leur équivalent diag, eyeetrand pour les matrices pleines.

Suivant: Calculer avec MATLAB Précédent: Présentation et généralités
Voir: Table des matière - Index - Accueil

(c) Stéphane Balac - Centre de Mathématiques - INSA de Lyon