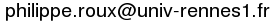Equations aux Différentielles Ordinaires et simulations avec Scilab
Principe de calcul d'une trajectoire
La trajectoire d'un objet dans la trajectoire d'un objet de masse m (ou plutôt son centre de gravité) est donnée par la suite des positions qu'il occupe au cours du temps : r(t)=(x(t),y(t)). Pour calculer les 2 coordonnées x et y de cette position on dispose en général d'une équation différentielle,le plus souvent obtenue par l'application de principes physiques simple (PFD, conservation del'énergie, ...), les dérivées premières de x et y correspondent aux coordonnées de la vitesse de l'objet et les dérivées secondes correspondent aux coordonnées de l'accélération de l'objet :
| équation du mouvement m * a(t)= F(t, r(t), v(t)) |
En général il est impossible de résoudre exactement une équation diférentielle aussi générale que celle qu'on peut rencontrer même avec des systèmes très simples. On cherche alors seulement à calculer à partir des valeurs r(t) v(t) a(t) les valeurs pour un temps t+dt avec dt « petit ». . Pour calculer f(t+dt) à partir de f(t) et f'(t) on utilise la formule f(t+dt)=f(t) +dt*f'(t) qui correspond à l'approximation, pour dt « petit » ,de la dérivée de f :
| f '(t)=df(t)/dt ~(f(t+dt)-f(t))/dt |
|
pour t=0 àT (avec pas de dt) faire
a(t+dt)=F(r(t),v(t))
fin_fairev(t+dt)=v(t)+dt*a(t) r(t+dt)=r(t)+dt*v(t) |
Dans la suite nous allons appliquer cette méthode à la résolution de quelques cas simples .
Le pendule simple
Le mouvement d'un pendule simple (i.e. Formé d'une masse m suspendue à une tige rigide de longueur l ) est entièrement décrit par la connaissance (en fonction du temps t) de l'angle a(t) formé par la tige et la verticale. Si on lache sans vitesse le pendule à partir d'un angle a(0) la fonction a(t) vérifie l'équation :
| d²a/dt²+w² * sin(a)=0 avec da(0)/dt=0, a(0) donné et avec w=(g/l)^(1/2) |
la valeur de a(t) peut être calculée par la méthode décrite ci-dessus :
|
a:= valeur initiale de l'angle du pendule avec la verticale
da:=0 valeur initiale de la vitesse angulaire du pendule dda:=0 valeur intiale de l'accélération angulaire du pendule
pour t=0 àT (avec pas de dt) faire
dda=-w^2*sin(a)
fin_faireda=da+dt*dda a=a+dt*da |
| d²a/dt²+w² * a=0 avec da(0)/dt=0, a(0) donné et avec w=(g/l)^(1/2) |
Les simulations suivantes pendule1.gif et pendule2.gif montrent comment cette approximation est juste pour a(0)<10° et fausse pour des angles importants ( éxécuter le fichier pendule.sce pour vérifier avec d'autres angles).
Le pendule élastique
dans le cas d'un pendule accroché à un ressort (de raideur k) les équations du mouvement deviennent très compliquées car cette fois la longueur du pendule r=r(t) varie en fonction de t et cette variation est couplée à celle de a(t)! Voici d'ailleur les équations du mouvement :
|
rd²a/dt²+2dr/dt * da/dt=g*sin(a) d²r/dt²-(k/m)*(r-r0)=r*(da/dt)²+g*cos(a) |
Le plateau oscillant
Une masse est posée sur un plateau animé d'un mouvement vertical périodique : z_0(t)=sin(w*t) . La masse est donc soumise à 2 forces : son poids P= -m*g et la réaction du plateau R. La réaction est soumise à 2 contraintes :
- tant que la masse reste sur le plateau (z=z_0) la somme des forces doit être égale à l'accélération du plateau (fois m) donc R=m*z_0''(t)-P.
- la réaction ne peut jamais être négative si celà arrive c'est que la masse se décolle du plateau (z>z_0) et donc R=0 et la seule force agissant sur lamasse m est son poids P
|
z_0:= fonction donnant le mouvement du plateau
z:=z_0(0) position initiale de l'object dz:= vitesse verticale de l'objet ddz:=0 accélération verticale de l'objet
pour t=0 àT (avec pas de dt) faire
R=m*z''_0(t)+m*g
si R<0 alors R=0 fin_si ddz= (R/m)-g dz=dz+dt*ddz z=z+dt*dz si z < z_0(t) alors z:=z_0(t) fin_si
fin_faire
|
En calculant l'accélération du plateau il est facile de voir que pour que R puisse prendre (potentiellement au moins) des valeurs négatives il faut que :
| -(w^2)*sin(w*t)+m*g<0 pour un certain t => w>(m*g)^(1/2) |
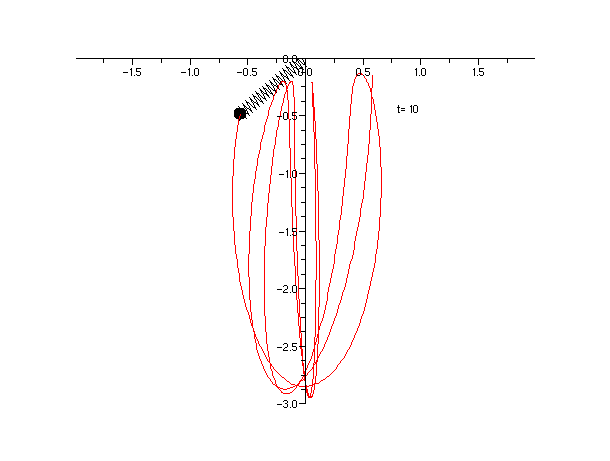
Dans les deux simulations ci-dessous m=1 et g=9.81 ce qui donne une valeur critique pour l'oscillation w= 3.132092 . Dans la première simulation on a fixé w=3 et la masse ne décolle pas dans la seconde on prend w=5 et au bout d'un certain temps on voit la masse décoller nettement du plateau. La procédure de base simul.sceet les animations simul1.gif et simul2.gif
Balle rebondissant dans une boite
Pour modéliser la trajectoire d'une balle qui rebondit dans une boite on considère qu'elle est soumise à son poids(plus un éventuel frottement avec l'air) et que ponctuellement elle subit des chocs (avec les parois de la boites). Ces chocs se traduisent par deux changements instantanés :
- l'accélération devient nulle au contact de la parois(à cause de la réaction de celle-ci)
- la partie de la vitesse perpendiculaire à la parois est réfléchie (modulo une petite perte si on veut tenir compte des frotements lors du choc).
En dehors des chocs la trajectoire (x(t),y(t)) de la balle peut être calculée en résolvant une équation de chute ``libre'' (accélération de la pesanteur g + c -> force de frotement proportionnelle à la vitesse ) :
| x''(t)=-c x'(t) et m z''(t)=-g-c z'(t) |
|
vitesse avant le choc v=(vx,vy)
choc sur un bord --> après le choc v'=(-vx,vy) choc sur le sol --> après le choc v'=(vx,-vy) |
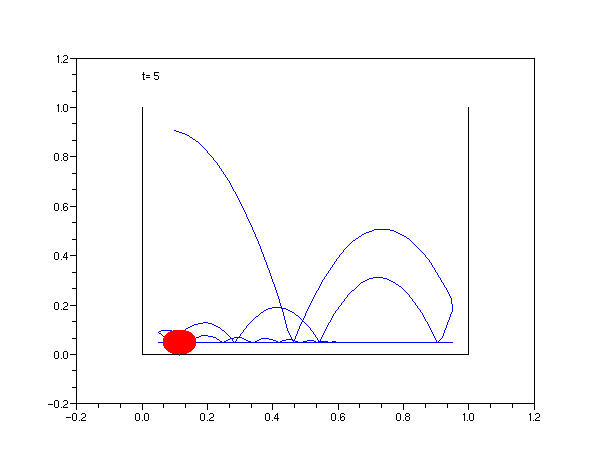
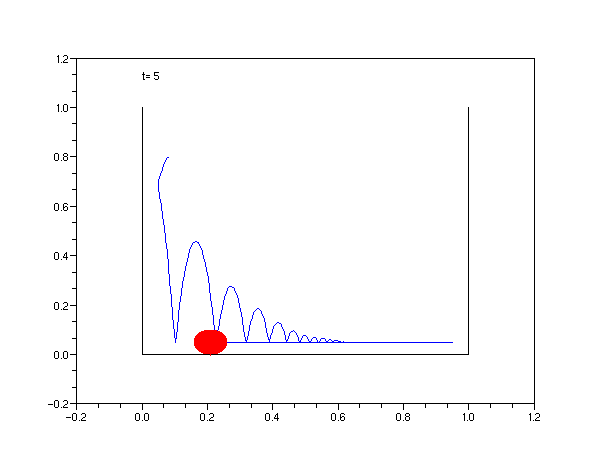
Voir aussi une animation de ce type avec plusieurs balles à l'adresse :
http://www.saphir-control.fr/articles/bouncing%20balls_lm29/article2.html