![]()
We consider the Laplace-Dirichlet equation in a polygonal domain which is perturbed at the scale epsilon near one of its vertices. We assume that this perturbation is self-similar, that is, derives from the same pattern for all values of epsilon.
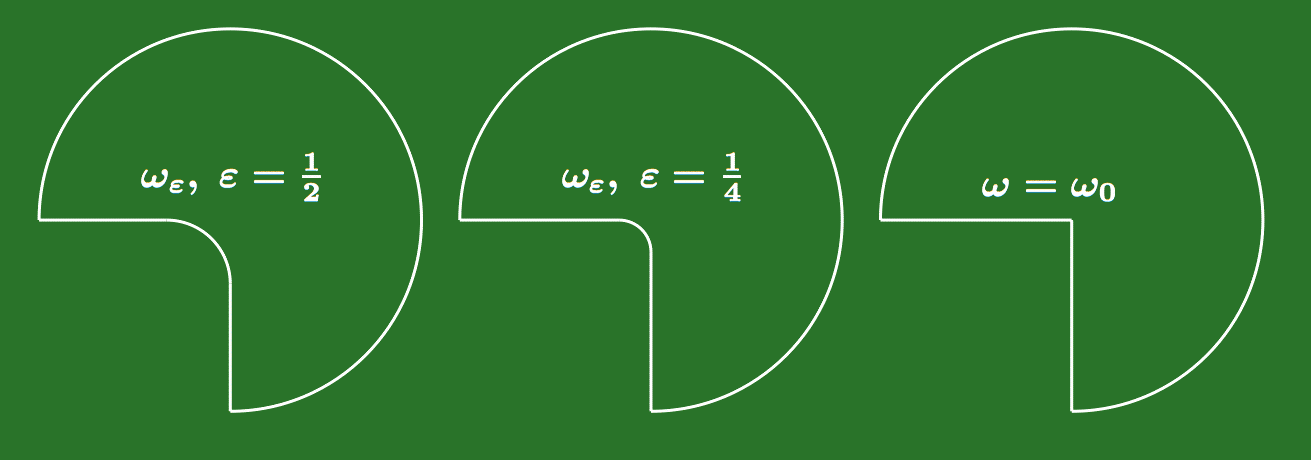
On the base of this model problem, we compare two different approaches for the investigation of solutions as epsilon --> 0 : the method of matched asymptotic expansions and the method of multiscale expansion. The two methods result in distinct expansions, each consisting of terms in slow variables, and terms in rapid variables. We give the formulas allowing to translate each expansion into the other one.
![]()
 |
Slides for the Bad Herrenalb Workshop on Composites, 28 November 2006: PDF file (128 k) |
|
Note CRAS:
PDF file (148 k)
C. R. Acad. Sc. Paris Ser. I 343 (2006), pp 637-642. |
![]()