![]()
Concerning thin structures such as plates and shells, the idea of reducing the equations of elasticity to two-dimensional models defined on the mid-surface seems relevant. Such a reduction was first performed thanks to kinematical hypotheses about the transformation of normal lines to the mid-surface: Let us mention, among others, the Kirchhoff-Love and Reissner-Mindlin models for plates, and the Koiter model for shells.
As nowadays, the asymptotic expansion of the displacement solution of the three-dimensional linear model is fully known at least for plates and clamped elliptic shells, we start from a description of these expansions in order to introduce the two-dimensional models known as hierarchical models: These models extend the classical models, and pre-suppose the displacement to be polynomial in the thickness variable, transverse to the mid-surface.
Because of the singularly perturbed character of the elasticity problem as the thickness approaches zero, boundary- or internal layers may appear in the displacements and stresses, and so may numerical locking effects. We describe how hierarchical models can be discretized by the p-version of finite elements, using refined meshes in the layer regions. Thanks to the very strong approximation properties of piecewise polynomials of high degrees in suitably designed anisotropic meshes, such a discretization may help to overcome locking effects.
Finally, besides the classical characterization of shells as membrane and flexural,
we also present a classification through the low frequency response of shells and give illustrative examples
of modal computations on three characteristic families:
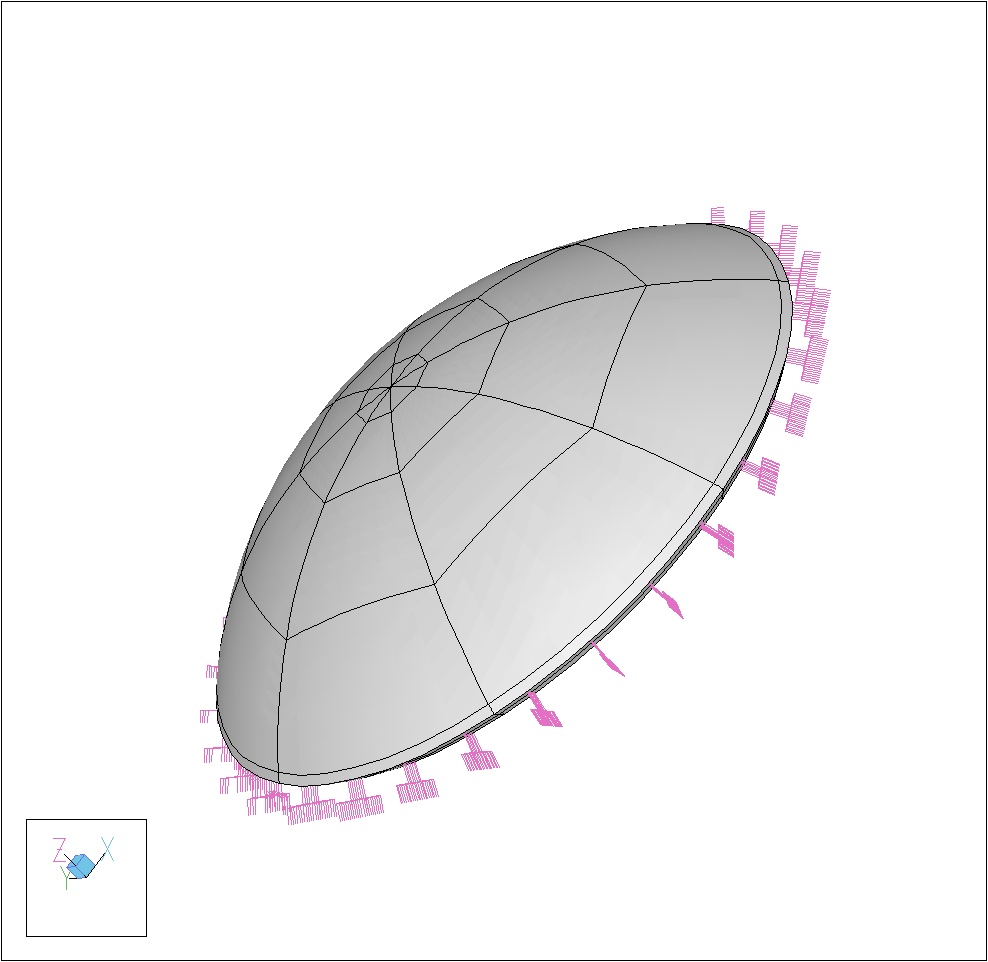
• Clamped spherical shells
• Partially clamped spherical shells (sensitivity)
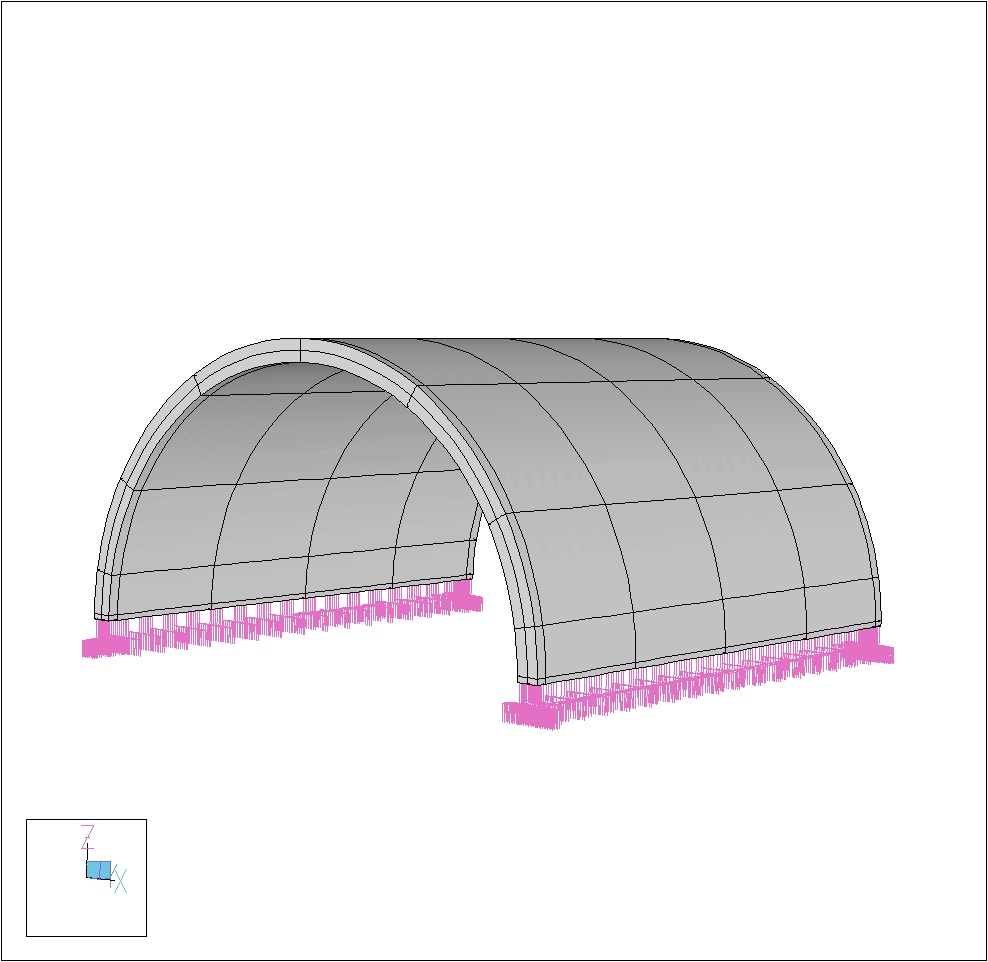
• Partially clamped cylindric shells (inextensional displacements)

![]()
February 2004.
Chapter 8,
Vol. I,
pp. 199-236, in the
Encyclopedia for Computational Mechanics
Edited by Erwin Stein, René de Borst, Thomas J.R. Hughes.
| Pdf file (4.2 MB) |
![]()