![]()
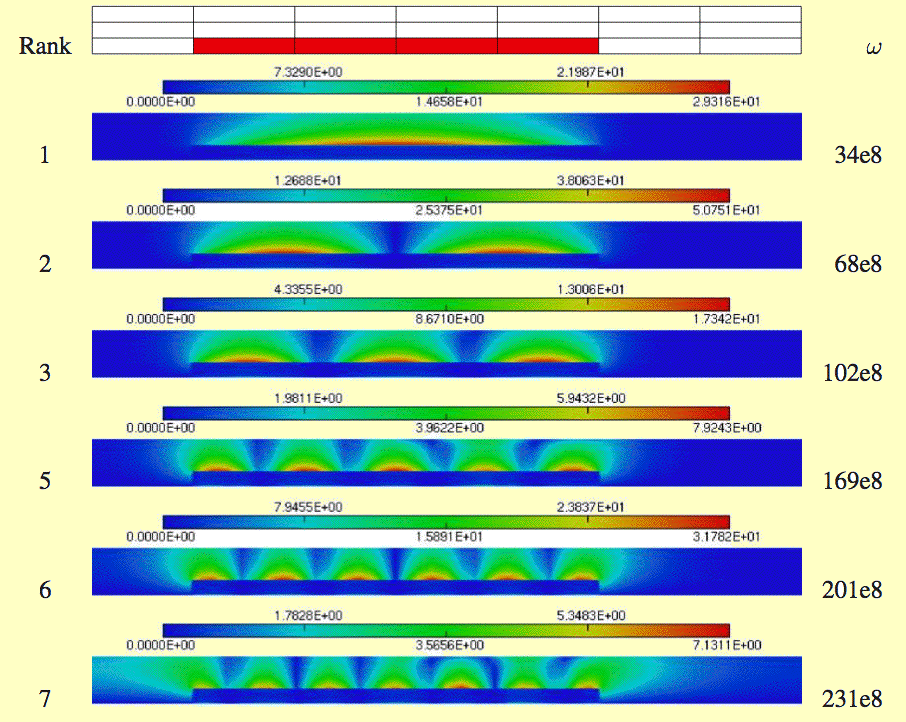
We study several mathematical and numerical models of resonance phenomena arising in Magnetic Resonance Imaging. We begin by describing eigenvalues and eigenfunctions of the Maxwell system with constant coefficients in a three-dimensional cylindrical domain. As particular cases, we find eigenpairs in a circular cylinder and in a circular cylinder with a coaxial circular hole. The corresponding eigenfrequencies give useful approximations of the resonance frequencies of a system consisting of a conducting wire embedded in homogeneous or heterogeneous physiological tissues encountered in MRI. We discretize this system with higher order finite elements and present computations describing the variations of the eigenfrequencies and of the structure of the eigenfunctions with respect to several relevant geometric and physical parameters.
![]()
| Preliminary version: PDF file (908 k) |