De la terminale à la fac: langage et exigence en mathématiques

A la recherche des expressions perdues



Retour

Voici une démonstration incomplète d'un exercice: il y manque des " expressions de liaison " figurant dans la liste ci-dessous:

Expression ainsi alors car comme de plus donc d'où et
N0 1 2 3 4 5 6 7 8 9

Expression il faut il suffit or par conséquent puisque si en effet
N0 10 11 12 13 14 15 16

Remarques:

L'exercice consiste à trouver les expressions manquantes dans la liste proposée.

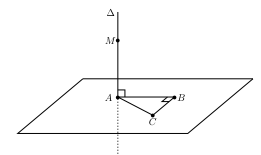
Exercice proposé au lycée

On considère un triangle ABC rectangle en B et Δ la droite perpendiculaire au plan (ABC) et passant par A.
Soit M un point de la droite Δ distinct de A. Montrer que les droites (BM) et (BC) sont perpendiculaires.		 

La droite (AM) est orthogonale à la droite (BC) ..........
une droite perpendiculaire à un plan est orthogonale à
toutes les droites de ce plan.
.............. le triangle ABC est rectangle en B,
........... (BC) et (AB) sont perpendiculaires,
........... (BC) est orthogonale à (AM);..........
 (BA) et (AM) sont sécantes. Pour qu'une droite
 soit perpendiculaire à un plan,
.......... elle soit orthogonale à deux droites sécantes de ce plan,
............ (BC) est perpendiculaire au plan (ABM)
.......... (BC) est perpendiculaire à (BM)
........... (BM) est contenue dans le plan (ABM).

Exercice proposé en DEUG

Montrer que les polynômes P1(X)=X(X-1)(X-2), P2(X)=X(X-1)(X-3), P3(X)=X(X-2)(X-3), P4(X)=(X-1)(X-2)(X-3) forment une base de R3[X].

......... R3[X] est un espace vectoriel de dimension 4,
poue prouver que la famille {P1,P2,P3,P4}
 est une base de R3[X], ......... vérifier qu'elle est libre.
............., dans un espace vectoriel de dimension 4,
toute famille libre de 4 vecteurs est une base de cet espace.
Soient λ1, λ2, λ3 et λ4 des nombres réels tels que
            λ1P1+λ2P2+λ3P3+λ4P4=0.
.........., on sait que, ............ P est le polynôme nul,
.......... pour tout réel a, on a P(a)=0.
.........., en prenant X=0, on obtient
            λ1.0+λ2.0+λ3.0+λ4.(-6)=0.
.......... λ4=0.
 De même, en prenant successivement X=1, on trouve
λ3=0, puis X=2, λ2=0, enfin X=3, λ1=0.
.......... λ1=λ2=λ3=λ4=0.
........., ces quatre polynômes forment une base de
R3[X], .....ils en forment une famille libre.

Autre exercice proposé en DEUG

Soit P appartenant à l'espace vectoriel Rn[X] des polynômes de degré inférieur ou égal à n. On pose u(P)=P+P'.
Montrer qu'on définit ainsi un endomorphisme de Rn[X].
Déterminer la matrice de u dans la base (1,X,X2,...,Xn).
Montrer que u est un automorphisme de Rn[X]. 
Tout d'abord, ....... deg(P)<deg(P'), le degré de u(P) est égal
au degré de P. ......., ....... P∈ Rn[X], on a u(P)∈ Rn[X].
De plus
 u(P1+P2)=(P1+P2)+(P1+P2)'=P1+P1'+P2+P2'=u(P1)+u(P2
et
     u(λP)=(λP)+(λP)'=λ(P+P')=λu(P).
....... u est bien un endomorphisme de Rn[X].
Pour obtenir les colonnes de la matrice M de u dans la base
(1,X,X2,...,Xn), il suffit de calculer les images par u des polynômes
de cette base:
u(1)=1, u(X)=X+1, u(X2)=X2+2X, ..., u(Xn)=Xn+nXn-1.
On obtient
            
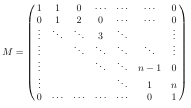Les vecteurs colonnes de la matrice de u forment un système de
générateurs de Im(u). De plus, ce système de
générateurs étant échelonné
inférieurement, c'est un système libre. Il est formé de n+1 vecteurs dans
l'espace vectoriel Rn[X] de dimension n+1. C'est ....... une base
et en particulier un système de générateurs de Rn[X].
On en déduit Im(u)=Rn[X]. ....... u est surjective, donc
c'est un isomorphisme de Rn[X], ......, pour qu'un endomorphisme
d'un espace vectoriel de dimension finie soit un isomorphisme
....... qu'il soit surjectif ou bien injectif.