Le modèle linéaire généralisé

 

 

 

Problème : estimer les paramètres du modèle     yi=b1x1i  + b2x2i + b3x3i +....bKxKi +ei
            
avec:
i = 1,...N,  N étant le nombre d'observations
yi : la variables expliquée  (variable endogène)
xki : les variables explicatives (variables exogènes) k = 1,...K
ei : un aléa

Sous forme matricielle lorsque le modèle comporte une constante, par exemple si x1i prend la valeur 1 quelque soit i=1,...N, le modèle s'écrit:

                  

                   


 Hypothèses :
            - les variables xki sont supposées non aléatoire
         - lorsque N tend vers l'infini l la matrice X'X/N est supposée être égale à une matrice définie positive (X' représente la transposée de la matrice)
         - ei est une variable aléatoire
         - E(ei)=0 ce qui implique que : E(yi)=b1x1i  + b2x2i + b3x3i +....bKxKi
            - la matrice de variance covariance des aléas est différente de s2I, les aléas peuvent être hétéroscédastique et ou autocorrélés

  

Lorsque la matrice de variance covariance des aléas est différente de s2I, l'estimateur des MCO est non biaisé mais il n'est pas efficace. Il existe un estimateur non biaisé des paramètres du modèle dont la variance est plus faible: l'estimateur des MCG.

L'estimateur des MCG est un estimateur des MCO sur un modèle transformé dont les aléas sont homoscédastiques et non autoccorélés (transformation d'Aitken). Soit V la matrice de variance covariance des aléas : l’estimateur des MCO du modèle suivant est BLUE :

 

L’estimateur des MCG est donné par l’expression suivante :

 

et sa matrice de variance covariance s’écrit :

Lorsque la matrice de variance covariance V  est inconnue, on doit chercher un estimateur convergent de W noté . On calcule dans ce cas l’estimateur des Moindres Carrés Quasi Généralisés (MCQG), estimateur convergent des paramètres du modèle.

L’estimateur des MCQG est donné par l’expression suivante :

 

et sa matrice de variance covariance s’écrit :

Deux cas particuliers sont usuellement présentés : le cas de l’hétéroscédasticité et le cas de l’autocorrélation d’ordre 1.

  

Si la variance des aléas n’est pas constante les aléas sont hétéroscédatiques var(ei)=s2i (pour détecter un problème d’hétéroscédasticité se reporter à la fiche sur les tests statistiques). Dans ce cas la matrice de variance covariance des aléas du modèle est donnée par :

                   

             

 

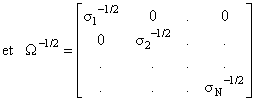
La méthode des MCG consiste alors à estimer avec la méthode des MCO le modèle suivant (on suppose que le modèle comporte une constante) :

           

 

Plus particulièrement, lorsque les tests d’hétéroscédasticité conduisent à retenir une hypothèse selon laquelle la variance des aléas dépend d’une variable explicative, on applique la méthode des MCO sur un modèle dont les observations sont rapportées à l’écart-type des aléas. Par exemple si on constate que var(ei)=s2x23i, le modèle transformé s’écrit :

 

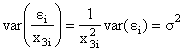
L’estimateur des MCG correspond à l’estimateur des MCO du modèle précédent :

           

 

 

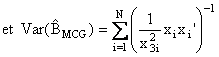
Les valeurs estimées de la variable endogène sont :

  

Lorsque les aléas sont autocorrélés d’ordre 1 (pour les tests se reporter à la fiche sur les tests statistiques) , c’est à dire lorsque  avec ui un aléa bruit blanc dont la variance est égale à , on doit appliquer la méthode des MCG car la matrice de variance covariance des aléas est différente de  s2I.

                      

 

 

 

 

La variance des aléas

 

 

 

 

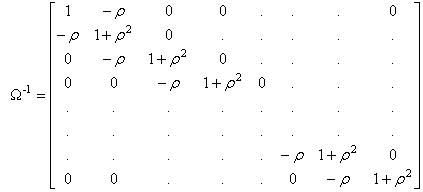
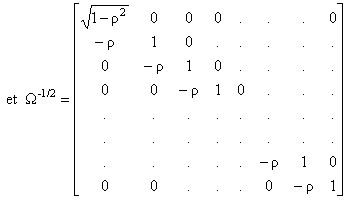
Ainsi, dans le modèle transformé on distingue la première observation pour laquelle :

et les observations i =2,….N pour lesquelles le modèle transformé est le modèle aux quasi différences :

           

L’estimateur des MCG correspond à l’estimateur des MCO sur le modèle transformé précédent, on obtient :

Cependant, généralement le coefficient d’autocorrélation est inconnu et par conséquent la matrice W est également inconnue. Il faut donc rechercher un estimateur convergent de r afin d’appliquer la méthode des moindres carrés quasi généralisés qui permet d’obtenir un estimateur convergent de B.

On dispose de plusieurs méthode d’estimation lorsque la matrice de variance covariance des aléas est inconnue. On distingue les méthodes qui utilisent les observations i = 1,….N et les méthodes qui utilisent les observations i = 2, ….N.

F La procédure de Prais-Winter utilise l’ensemble des observations. Dans cette procédure le coefficient d’autocorrélation est calculé de manière à minimiser la fonction suivante :

 

 

avec e le vecteur des résidus du modèle Y=XB+e estimé avec la méthode des MCO.

La méthode de Prais-Winter consiste dans un premier temps à estimer le modèle avec la méthode des MCO et à calculer la valeur estimée du coefficient d’autocorrélation. Dans un second temps on réestime le modèle avec la méthode des Moindres carrés quasi généralisés avec :

 

 

 

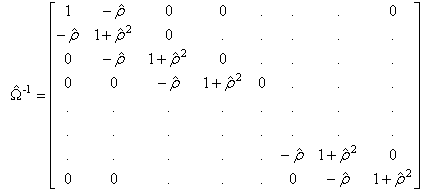
On peut appliquer une procédure itérative en recalculant une valeur de r à partir des résultats d’estimation du modèle précédent.

F La méthode du maximum de vraisemblance repose sur la maximisation du logarithme de la fonction de vraisemblance

               

 

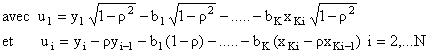
F La procédure de Cochrane Orcutt  utilise les observations i =2,…N. Dans cette procédure le coefficient d’autocorrélation est calculé de manière à minimiser la fonction suivante :

 

avec e le vecteur des résidus du modèle Y=XB+e estimé avec la méthode des MCO.

 La méthode de Cochrane Orcutt consiste dans un premier temps à estimer le modèle avec la méthode des MCO et à calculer la valeur estimée du coefficient d’autocorrélation.

Dans un second temps on réestime le modèle avec la méthode des Moindres carrés quasi généralisés, autrement di on estime avec la méthode des MCO le modèle quasi-différencié :

           

 

On peut appliquer une procédure itérative en recalculant une valeur de r à partir des résultats d’estimation du modèle précédent.

F La méthode de Hildreth-Lu utilise également un nombre d’observation i = 2,…N. On applique les MCO de manière répétée sur le modèle quasi différencié en prenant différentes valeurs du coefficient d’autocorrélation comprises entre -1 et 1. On choisit la valeur de r qui minimise la somme des carrés des résidus du modèle estimé.

Dans un modèle dont les aléas sont autocorrélés d'ordre 1,  la prévision optimale de y à la période N+1 est :