Sur les singularités cuspidales.

On appelle singularité cuspidale tout germe de feuilletage singulier
défini par un champ de vecteurs à singularité isolée à l'origine
du plan complexe, dont la partie linéaire est nilpotente et la partie
quadratique générique. Dans ce cas, il possède
une unique courbe analytique invariante à l'origine qui se redresse
sur le cusp
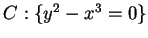 par changement de coordonnées locales.
Par exemple, le feuilletage singulier défini par le champ
par changement de coordonnées locales.
Par exemple, le feuilletage singulier défini par le champ
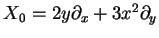 d'intégrale première
d'intégrale première
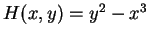 est cuspidal ainsi que toute
perturbation cubique de celui-ci.
est cuspidal ainsi que toute
perturbation cubique de celui-ci.
En particulier, l'espace des modules est énorme (de dimension infinie).
On peut facilement déduire, à l'aide du Théorème de Baire,
l'existence de singularités (cuspidales) qui ne sont polynomiale dans aucun système
de coordonnées locales. L'existence de telles
singularités non algébrique n'était pas établie
jusqu'à ce jour, à ma connaissance. Du coup, le résultat
antérieur ci-dessous montre que la topologie des singularités
cuspidales est très variée.
Théorème (1995) :
Toute singularité cuspidale
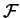 est rigide :
si un germe d'homéomorphisme
est rigide :
si un germe d'homéomorphisme
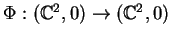 envoit les feuilles de
envoit les feuilles de
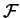 sur celles
d'une autre singularité de feuilletage holomorphe
sur celles
d'une autre singularité de feuilletage holomorphe
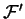 alors ces deux singularités
se correspondent aussi par un changement de coordonnées holomorphe ou
anti-holomorphe.
alors ces deux singularités
se correspondent aussi par un changement de coordonnées holomorphe ou
anti-holomorphe.
|
|



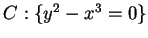 par changement de coordonnées locales.
Par exemple, le feuilletage singulier défini par le champ
par changement de coordonnées locales.
Par exemple, le feuilletage singulier défini par le champ
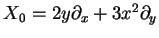 d'intégrale première
d'intégrale première
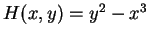 est cuspidal ainsi que toute
perturbation cubique de celui-ci.
est cuspidal ainsi que toute
perturbation cubique de celui-ci.

