Un théorème de préparation pour les feuilletages.

Ce travail est initialement motivé par le problème suivant.
Étant donné un germe de champ de vecteur analytique
à l'origine du plan complexe
trouver un système de coordonnées analytiques locales
dans lequel les coefficients du champ de vecteur sont les plus simples possibles.
C'est en essayant de comprendre un résultat de J. Écalle allant
dans cette direction (voir plus bas) que j'ai découvert la chose suivante.
Dans ce genre de problème, chercher à simplifier les coefficients
revient souvent à chercher un représentant (dans la classe de conjugaison)
admettant un prolongement analytique maximal avec le mois de singularités possibles.
Par exemple, lorsque l'on cherche une forme normale polynomiale,
on cherche en fait un représentant admettant un prolongement analytique
(ou plutôt méromorphe) sur tout le plan projectif complexe !
Les formes normales de Dulac sont les modèles polynomiaux
qui admettent le moins de singularités, c'est à dire dont le feuilletage
global est le plus simple. De la même manière, la forme normale
de Bogdanov-Takens pour les singularités nilpotentes, dont l'analyticité
a été prouvée par E. Strozyna et H. Zoladek, est polynomiale
dans la variable 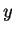 avec degré minimal : le champ de vecteur admet un prolongement
analytique sans fin le long de l'axe vertical, régulier dans la partie finie
et avec un pôle simple à l'infini. Ce genre de résultat se démontre
habituellement par un procédé itératif de changements de coordonnées
(analytiques ou polynomiales) dont il faut contrôler la convergence.
C'est souvent long et difficile. L'idée que j'ai eu est de redémontrer
ces théorèmes de manière géométrique, en construisant
le prolongement analytique par recollement de variétés complexes,
puis par uniformisation. avec degré minimal : le champ de vecteur admet un prolongement
analytique sans fin le long de l'axe vertical, régulier dans la partie finie
et avec un pôle simple à l'infini. Ce genre de résultat se démontre
habituellement par un procédé itératif de changements de coordonnées
(analytiques ou polynomiales) dont il faut contrôler la convergence.
C'est souvent long et difficile. L'idée que j'ai eu est de redémontrer
ces théorèmes de manière géométrique, en construisant
le prolongement analytique par recollement de variétés complexes,
puis par uniformisation.
Le premier résultat que j'obtiens est un "Théorème de Préparation"
pour les feuilletage de codimension 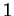 . Notons . Notons
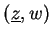 la variable de
la variable de
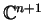 avec avec
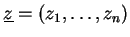 , , 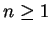 . .
La preuve peut se résumer dans la figure suivante :
Après normalisation, le feuilletage est défini sur un voisinage tubulaire
de la droite projective verticale
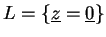 dans dans
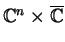 ,
il est régulier et transverse à ,
il est régulier et transverse à 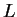 en dehors de l'origine. en dehors de l'origine.
|





