| |
Connaissances |
Licence de Rennes 1 |
| Analyse |
| 
|
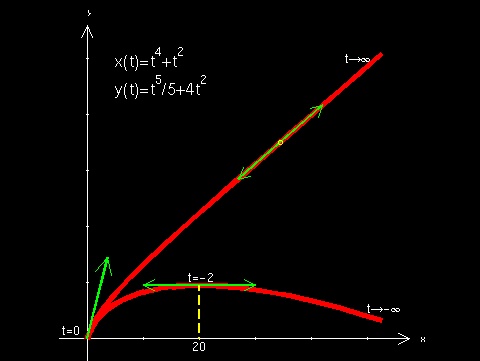
 Analyse
de base : étude de fonctions (continuité,
dérivabilité, formule de Taylor et développements
limités, convexité, branches infinies, fonctions
classiques), nombres complexes, suites et séries,
intégrale de Riemann et primitives, équations
différentielles (premier et second ordre) linéaires
et à variables séparées (équation
homogène, variation de la constante). |
|
A01 - Nombres réels et complexes.
Fonctions classiques.
B01 - Étude locale des fonctions.
B02 - Suites et séries. Primitives
C01. Étude globale des fonctions, intégration.
C02 - Étude de fonctions. Équations
différentielles
D02 - Suite et séries de fonctions |
| |
 Fonctions
de plusieurs variables : continuité, dérivées
partielles, matrice jacobienne, différentielle, intégrale
curviligne, intégrale multiple, surfaces. |
|
D01 - Fonctions de plusieurs variables, intégrales
multiples, courbes paramètrées |
| |
 Équations
différentielles : existence et unicité d'une
solution (théorème de Cauchy-Lipschitz), méthodes
numériques (Euler explicite et implicite, Adams,
convergence et stabilité). |
|
F01 - Équations différentielles
(ou en M1) |
| |
 Intégrale
de Lebesgue : définition, théorème de
convergence dominée, exemples, techniques de calcul. Intégrale
de Lebesgue : définition, théorème de
convergence dominée, exemples, techniques de calcul. |
|
C01. Étude globale des fonctions,
intégration.
(éventuellement E03 - Intégration
et probabilités ou F02 - Intégrale
de Lebesgue et séries de Fourier ou
en M1) |
| |
 Analyse
fonctionnelle hilbertienne: espaces vectoriels normés,
espaces de Banach (complétude, espaces l p
et L p, inégalités de Hölder
et Minkowski), espaces de Hilbert. |
|
F07 - Analyse fonctionnelle hilbertienne |
| Algèbre |
| |
 Algèbre
linéaire : espaces vectoriels (définition,
exemples, sous-espaces vectoriels, famille libre et génératrice,
base, dimension, rang, somme de sous-espaces vectoriels,
produit), applications linéaires (définition,
composition, inverse, exemples, noyau, image, injectives,
surjectives, bijectives, rang, formes linéaires)
et matrices (produits, changement de base, trace, valeurs
propres et vecteurs propres, sous-espaces propres, déterminant,
diagonalisation et triangulation), systèmes linéaires
(existence et unicité d'une solution, pivot de gauss). |
|
B04 - Espaces vectoriels et applications
linéaires.
C05 - Matrices et systèmes linéaires. |
| |
 Algèbre
multilinéaire : applications multilinéaires,
formes bilinéaires, formes quadratiques, produits
scalaires, inégalité de Cauchy-Schwartz, orthonormalisation
de Schmidt, norme euclidienne, produit vectoriel. |
|
D03 - Algèbre multilinéaire |
| Méthodes numériques |
| |
 Méthodes
numériques élémentaires : Résolution
d'équation non linéaires (dichotomie, méthode
de Newton, méthode de la sécante, contraction
et théorème du point fixe), Interpolation
polynômiale (Lagrange, Newton, Hermite) et Intégration
numérique (méthode des trapèzes, de
Simpson, composées, de gauss). |
|
C03 - Méthodes numériques
en analyse |
| |
 Méthodes
numériques de résolution de systèmes
linéaires (méthodes directes: Gauss, factorisation
LU, Cholesky, factorisation QR, Householder; méthodes
itératives: Jacobi, Gauss-Seidel, relaxation) et
de recherche d'éléments propres (Jacobi, Givens-Householder,
QR). |
|
F04 - Algèbre linéaire
numérique |
| |
|
|
| |
|
|
Dernière mise
à jour :
3/4/08
par Fabrice Mahé |