A stiffly stable fully discrete scheme for the damped wave equation using discrete transparent boundary condition

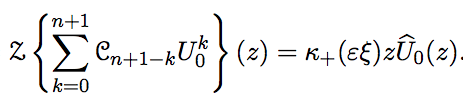
Résumé

We study the stability analysis of the time-implicit central differencing scheme for the linear damped wave equation with boundary. Xin and Xu (J. Differential Equations 2000) prove that the initial-boundary value problem (IBVP) for this model is well-posed, uniformly with respect to the stiffness of the damping, under the so-called stiff Kreiss condition (SKC) on the boundary condition. We show here that the (SKC) is also a sufficient condition to guarantee the uniform stability of the discrete IBVP for the relaxation system independently of the stiffness of the source term, of the space step and of the time step. The boundary is approximated using discrete transparent boundary conditions and the stiff stability is proved using energy estimates and the Z−transform.