Coupling techniques for nonlinear hyperbolic equations. III. The well-balanced approximation of thick interfaces.

Résumé

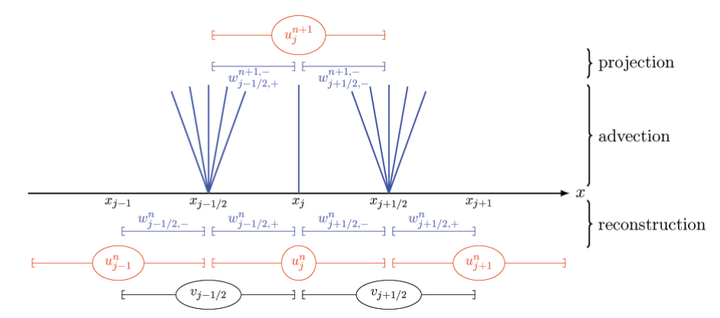
We continue our analysis of the coupling between nonlinear hyperbolic problems across possibly resonant interfaces. In the first two parts of this series, we introduced a new framework for coupling problems which is based on the so-called thin interface model and uses an augmented formulation and an additional unknown for the interface location; this framework has the advantage of avoiding any explicit modeling of the interface structure. In the present paper, we pursue our investigation of the augmented formulation and we introduce a new coupling framework which is now based on the so-called thick interface model. For scalar nonlinear hyperbolic equations in one space variable, we observe that the Cauchy problem is well-posed. Then, our main achievement in the present paper is the design of a new well-balanced finite volume scheme which is adapted to the thick interface model, together with a proof of its convergence toward the unique entropy solution (for a broad class of nonlinear hyperbolic equations). Due to the presence of a possibly resonant interface, the standard technique based on a total variation estimate does not apply, and DiPerna?s uniqueness theorem must be used. Following a method proposed by Coquel and LeFloch, our proof relies on discrete entropy inequalities for the coupling problem and an estimate of the discrete entropy dissipation in the proposed scheme.