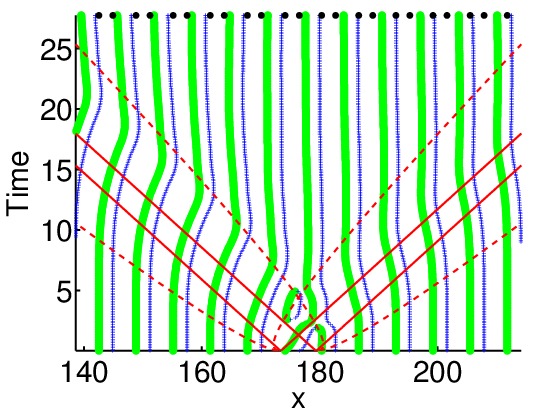
Suivi des déphasages par les pics (en vert) et les creux (en bleu). Comparaison avec la dynamique moyennée (en rouge).
| Contact | C.V. (vitæ) | Enseignement | Recherche (research) |
|---|---|---|---|
| Habilitation | Présentation | (Pré)publications | Thèse |
|---|---|---|---|
Les travaux présentés pour me gagner une habilitation à diriger des recherches ont été préparés au sein du thème « Modélisation Mathématique et Calcul Scientifique » de l'Institut Camille Jordan (Lyon 1). Après des rapports de François Hamel, David Lannes et Robert Pego, elle a été soutenue le 9 décembre 2013 devant Sylvie Benzoni-Gavage, Thierry Gallay, François Hamel, David Lannes, Guy Métivier, Guido Schneider et Denis Serre.
Outre la présentation du mémoire lui-même --- intitulé Asymptotic stability and modulation of periodic wavetrains. General theory & applications to thin film flows ---, vous trouverez ci-dessous une description succinte de ces travaux.
L'essentiel de ces travaux est né de la synergie entre un pôle lyonnais --- constitué de Pascal Noble (maintenant professeur à l'INSA Toulouse) et moi-même et financé par le projet A.N.R. Shallow Water Equations for Complex Fluids --- et un pôle bâti autour de Kevin Zumbrun (Indiana, États-Unis) et constitué de lui-même, de Blake Barker, son doctorant, et de Mathew A. Johnson, alors son post-doctorant et désormais assistant professor de l'Université du Kansas.
Ci-dessous la désignation de mes travaux se réfère à ma liste de publications en ligne.
Une des stratégies classiques pour appréhender des phénomènes complexes consiste à identifier des structures cohérentes autour desquelles s'organise la dynamique. Parmi ces motifs élémentaires, les ondes --- et plus particulièrement les ondes périodiques --- se retrouvent de fait au cœur de certains champs disciplinaires : acoustique, électromagnétisme, hydrodynamique, combustion, propagation biologique... Ainsi, les ondes périodiques jouent pour certains systèmes d'équations aux dérivées partielles un rôle comparable à celui des cycles périodiques, longuement étudiés par Gaston Floquet et Henri Poincaré, pour la dynamique bi-dimensionnelle. Au delà des préoccupations purement théoriques, une connaissance profonde de la dynamique autour de ces structures particulières a engendré tout au long du vingtième siècle des percées technologiques majeures. Ainsi, la découverte que la dynamique autour des ondes périodiques pouvaient supporter des ondes de modulation en paramètres a révolutionné les télécommunications. Cet impact est encore reflété par la distinction modulation d'amplitude (AM)/ modulation de fréquences (FM) des communications radio.
Malgré son importance pratique et fondamentale et le fait que la mise en place d'expériences de laboratoire fines et la conception d'objets technologiques perfectionnés ont depuis longtemps été accompagnées de théories formelles élaborées, par bien des aspects jusqu'il y a peu nous n'en étions qu'aux balbutiements d'une théorie mathématique pour l'analyse de la dynamique non linéaire autour des trains d'ondes périodiques. L'un de mes buts originels au moment d'engager la série de travaux ici présentés était donc pour les systèmes (partiellement) paraboliques d'équations aux dérivées partielles de mettre la connaissance mathématique des ondes périodiques au niveau de celle de structures plus simples et mieux connues comme les fronts ou les ondes solitaires.
Par opposition à ce qui se passe autour de ces structures --- au premier ordre la dynamique y est asymptotiquement en temps capturée par l'introduction de paramètres de modulation uniformes en espace et donc réduite à la dimension finie ---, la dynamique autour des ondes périodiques est fondamentalement multi-échelle et de dimension infinie, comme le prouve l'existence d'ondes de diffusion en paramètres. Cette différence conduit à de grandes difficultés techniques mais également à des obstacles conceptuels.
Nous avons ainsi dû identifier une notion de stabilité adéquate, la stabilité modulée en espace, qui est le pendant de la stabilité orbitale des fronts et des ondes solitaires. Nous montrons alors un résultat que l'on peut énoncer en termes vagues comme
Théorème. Dans un système parabolique, une onde périodique linéairement stable --- au sens de la stabilité spectrale diffusive --- est également non linéairement asymptotiquement stable --- au sens, modulé en espace, de Lyapunov. De plus les taux de retour sont algébriques en temps.
La notion de stabilité modulée en espace répond aux observation suivantes. Une onde stable résorbe les perturbations en faisant légèrement varier en temps et en espace les paramètres qui la définissent comme élément d'une famille d'ondes, ces variations voyageant essentiellement le long de lignes droites données par les vitesses de groupe linéaires en paquets diffusifs de type Burgers ou chaleur qui intéragissent faiblement. Chaque passage d'une telle onde de diffusion en paramètres résulte en la création d'un déphasage qui persiste. Ainsi au premier ordre la création d'ondes de diffusion en paramètres se manifeste par la découpage des diagrammes temps-espace en cônes séparés par des zônes d'intéraction diffusives et à l'intérieur desquels on retrouve des portions de l'onde originale dont les déphasages différent de cône à cône.
En résumant grossièrement on peut dire que l'introduction d'une perturbation crée un objet qui ne diffère de l'onde initiale que par un changement de variables qui n'est que translations uniformes par morceaux. Un moyen de quantifier cela consiste à mesurer (à un temps donné) l'éloignement d'une fonction de l'espace \(u\) à une autre \(v\) dans un espace fonctionnel donné \({\mathcal H}\) non pas directement par \(\|u-v\|_{{\mathcal H}}\) mais par $$ \inf_{\Psi \textrm{ bijectif}}\ \|u\circ\Psi-v\|_{{\mathcal H}}\,+\,\|\partial_x(\Psi-{\rm Id}_\mathbf{R})\|_{{\mathcal H}}\,. $$ Ceci conduit à la notion de stabilité modulée en espace.
Pour des ondes périodiques (diffusivement) spectralement stables, nous avons également fourni une description fine du comportement en temps long en validant et complétant la théorie de la modulation faiblement non linéaire. Cela permet de décrire la dynamique autour d'une onde stable --- et en particulier de confirmer, quantifier et compléter le scénario esquissé plus haut --- à partir de celle de ses paramètres locaux (parmi lesquels le nombre d'ondes local, dérivée de la phase locale) qui s'organise autour de solutions constantes stables --- les paramètres de l'onde de référence --- d'un système moyenné.
Le système moyenné peut s'obtenir relativement simplement par une approche purement formelle basée sur des développements multi-échelles. Mais le scénario complet nécessite l'obtention de données initiales équivalentes qu'une telle analyse heuristique ne fournit pas et que seule l'analyse mathématique révèle.

Nos analyses ont d'abord été mises en place pour les cas où le système moyenné, appelé système de Whitham, est en fait une équation scalaire [6,7] avant d'être portées pour le cas général [10]. Notons que pour le cas scalaire une autre approche est possible --- Björn Sandstede, Arnd Scheel, Guido Schneider et Hannes Uecker. Nonlocalized modulation of periodic reaction diffusion waves: nonlinear stability, Journal of Differential Equations , Vol. 5, no. 252 (2012), p.3541-3574 --- puisque l'une des échelles du problème --- l'échelle hyperbolique --- disparaît, de sorte que la dynamique moyennée est essentiellement invariante d'échelle et que l'analyse peut procéder des techniques de l'auto-similarité telle que la renormalisation.
Dans le cadre du projet A.N.R. Blanc Boundaries, Numerics, Dispersion porté par Sylvie Benzoni-Gavage (Lyon 1), entre autres choses nous visons à terme l'extension de ces résultats aux systèmes dispersifs hamiltoniens, avec comme motivation l'application aux fluides capillaires non visqueux. Les premières avancées dans cette direction sont pour l'instant uniquement spectrales [11].
Dresser des diagrammes de stabilité spectrale de certains écoulements particuliers constitue l'un des archétypes d'axes d'étude en dynamique des fluides. Le principe en est que les équations même adimensionnées contiennent encore un certain nombre de paramètres (nombres de Reynolds, de Mach, de Rayleigh, de Prandtl, de Froude...) et que la stabilité --- et parfois même l'existence --- de certains types d'écoulements dépend crucialement des valeurs de ces nombres.
Par ailleurs, par un phénomène de bifurcation, à la transition stabilité/instabilité, on s'attend à l'apparition de nouvelles structures particulières, de complexité dimensionnelle plus grande, dont on peut également étudier la stabilité... La stratégie classique est alors de partir d'une famille de solutions simples voire triviales que l'on sait stables dans un certain régime des paramètres du système puis de varier ces paramètres tout en suivant à la fois la stabilité spectrale des écoulements triviaux et celle des nouvelles familles de solutions apparaissant aux transitions. Les nouvelles solutions émergeant de la première transition sont usuellement appelées instabilités primaires, celles apparaissant après une de leurs transitions vers l'instabilité instabilités secondaires. Usuellement à cause de la montée en complexité dimensionnelle par brisure de symétries, après la seconde instabilité viennent chaos puis turbulence.
Nous avons partiellement mené une telle étude pour la description des films minces de fluide s'écoulant le long d'une pente lisse. Les écoulements simples présentent une surface parallèle à la pente et l'on s'attend à ce qu'ils soient stables pour des pentes modérées. Leurs instabilités primaires exhibent des surfaces supportant des ondes progressives périodiques planes appelées rouleaux. La surface des instabilités secondaires supporte des ondes progressives bi-périodiques en échiquier. Signalons incidemment que tous ces motifs sont facilement observables le long des rues pentues par temps pluvieux.

Dans la limite de faible épaisseur, il est classique d'approcher la dynamique des films minces, incompressible et à surface libre, par une dynamique réduite en dimension qui ne suit l'écoulement que par la hauteur de sa surface \(h\) et une moyenne en épaisseur \(u\) de sa composante longitudinale. Pour notre problème cela conduit à un système, de type Navier-Stokes compressible, appelé système de St Venant, \begin{equation}\label{SV}\tag{SV} \left\{\begin{array}{l} \partial_th +\partial_x (h\,u)\,=\,0\,,\\[5pt] \partial_t(h\,u)+\partial_x(h\,u^2\,+\,\tfrac12\,\tfrac{h^2}{\mathbf{F}^2})\,=\,h\,-\,|u|\,u\,+\,\partial_x(h\,\partial_xu)\,, \end{array}\right. \end{equation} qui prend en compte des effets de gravité et de viscosité et de frottement turbulents. Le système contient un nombre sans dimension \(\mathbf{F}\) donné par la racine carrée du quotient de la pente par un certain coefficient de frottement et appelé nombre de Froude. Les instabilités primaires mentionnées ci-dessus apparaissent alors pour \(\mathbf{F}>2\) et sont décrites comme des ondes progressives planes périodiques du système. Proche du seuil d'instabilité \(\mathbf{F}=2\), on peut chercher à encore réduire la complexité de la description. On est alors conduit vers une équation scalaire, l'équation de Korteweg--de Vries/Kuramoto-Sivashinsky \begin{equation}\label{KS}\tag{KdV-KS} \partial_tv\,+\,\partial_x(\tfrac12\,v^2)\,+\,\partial_x^3v\ =\ -\delta\,(\partial_x^2v+\partial_x^4v)\, \end{equation} avec \(\delta\sim\sqrt{\mathbf{F}-2}\). Bien que le domaine de validité de cette dernière description soit réduit, le modèle a l'avantage d'être canonique de sorte que son étude livre des informations sur une infinité de situations analogues.
Notons au passage que contrairement à ce que l'on pourrait penser à première vue, l'étude des films minces est une question cruciale par son ubiquité. On trouve ainsi des écoulements de faible ratio d'aspect aux niveaux géophysique (océans, atmosphère, fleuves...), physiologique (cornée, muqueuses, poumon...) ou industriel (moulage, lubrification...).
En parallèle du développement d'une théorie générale capable d'exploiter des informations spectrales suffisamment précises, nous nous sommes attachés à étudier aussi complétement et analytiquement que possible la stabilité spectrale diffusive des ondes périodiques de \eqref{KS} et \eqref{SV} représentant les instabilités hydrodynamiques primaires appelées rouleaux.
Au préalable nous avions discuté avec une combinaison d'arguments analytiques et numériques dans [ 4] les remarquables propriétés de stabilité des trains infinis d'ondes solitaires associées, et ce alors que ces ondes prises isolément sont radicalement mais convectivement instables.
La détermination de la stabilité diffusive implique l'analyse du spectre d'un opérateur différentiel à coefficients périodiques agissant sur des fonctions définies sur toute la ligne. Sous des hypothèses relativement faibles, on peut montrer que ces spectres sont purement essentiels mais peuvent être décomposés grâce à une transformation intégrale adéquate --- la transformation de Floquet-Bloch --- en spectres discrets --- ceux des symboles de Bloch, des opérateurs différentiels à coefficients périodiques agissant sur des fonctions de même période --- paramétrés par des exposants de Floquet variant continûment dans la zône de Brillouin.
La stabilité diffusive requiert non seulement que le spectre du générateur de la dynamique linéarisée autour de l'onde considérée soit entièrement contenu dans le demi-plan fermé à gauche de l'axe imaginaire pur mais également, en un sens que nous ne détaillerons pas ici, que cette stabilité soit aussi forte que possible et que le paramétrage par les exposants de Floquet soit aussi peu dégénéré que possible comptes tenus de l'existence d'une famille d'ondes périodiques autour de l'onde de référence.
Déterminer analytiquement pour toute onde périodique des propriétés spectrales aussi fines est évidemment hors de portée. Aussi pour dresser des diagrammes complets de stabilité diffusives pour les ondes de \eqref{KS} [9] et de \eqref{SV} nous avons conjugué des arguments analytiques basés essentiellement sur des diagonalisations asymptotiques et permettant de confiner la recherche d'une partie éventuellement instable du spectre à une zône bornée du plan complexe et des évaluations numériques de nombres de rotation ou de coefficients de Taylor de certaines fonctions d'Evans.
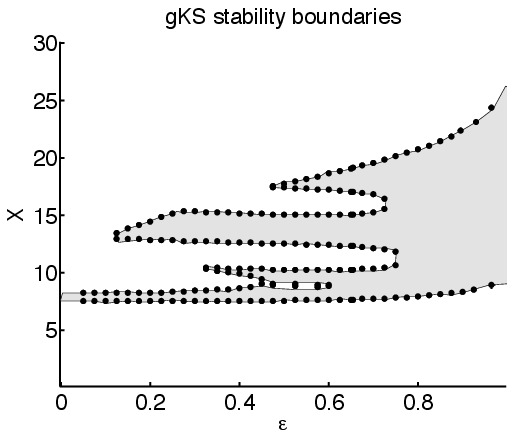
À défaut d'études complètes essentiellement analytiques, on peut espérer de telles études dans certains régimes asymptotiques. Dans cet esprit nous avons étudié ce qu'il se passe proche des seuils d'instabilité primaire, la limite \(\delta\to0^+\) pour \eqref{KS} [5,8], \(\mathbf{F}\to2^+\) pour \eqref{SV}.
Dans cette limite les ondes émergent de certaines ondes cnoïdales de l'équation de Korteweg--de Vries \begin{equation}\label{KdV}\tag{KdV} \partial_tv\,+\,\partial_x(\tfrac12\,v^2)\,+\,\partial_x^3v\ =\ 0\,. \end{equation} Ces ondes cnoïdales sont spectralement stables au sens faible, associé au caractère hamiltonien de \eqref{KdV}, que le spectre du générateur de la dynamique linéarisée autour de l'onde considérée coïncide avec l'axe imaginaire. Comme on le constate sur un diagramme complet de stabilité, seule une bande de telles ondes cnoïdales génère des ondes diffusivement stables pour \eqref{KS}. Nous avons quantifié et prouvé ce fait en introduisant un indice de persistance de stabilité \(\textrm{Ind}\) menant à un résultat grossièrement énoncé comme suit.
Théorème. Une onde cnoïdale de \eqref{KdV} vérifiant \(\textrm{Ind}<0\) génère des ondes diffusivement spectralement stables pour \eqref{KS}.
Il en est de même pour \eqref{SV}. Cet indice est par ailleurs relativement facile à évaluer numériquement et les calculs nécessaires à cette évaluation, déjà disponibles --- Doron E. Bar et Alexander A. Nepomnyashchy. Stability of periodic waves governed by the modified Kawahara equation. Physica D, 86(4): 586-602, 1995 ---, sont en adéquation avec les diagrammes complets de stabilité.