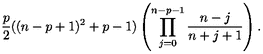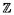 : S0 = 0, et Sn =
: S0 = 0, et Sn = 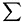 i = 1nXi, pour n > 1, où (Xi)i>1 est une
suite de variables aléatoires i.i.d., telles que
i = 1nXi, pour n > 1, où (Xi)i>1 est une
suite de variables aléatoires i.i.d., telles que 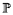 [X1 = 1] =
[X1 = 1] = 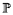 [X1 = -1] = 1
2.
[X1 = -1] = 1
2.
Soit (Si )i>1 une marche aléatoire simple sur 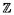 : S0 = 0, et Sn =
: S0 = 0, et Sn = 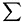 i = 1nXi, pour n > 1, où (Xi)i>1 est une
suite de variables aléatoires i.i.d., telles que
i = 1nXi, pour n > 1, où (Xi)i>1 est une
suite de variables aléatoires i.i.d., telles que 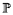 [X1 = 1] =
[X1 = 1] = 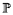 [X1 = -1] = 1
2.
[X1 = -1] = 1
2.
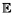 [(Sn)2].
[(Sn)2].
Prendre différentes valeurs de n et de MC (MC=100, 1000, 10000). Pour éviter la recompilation à chaque changement de valeurs, on pourra définir les paramètres n et MC comme des variables à entrer au clavier.
Les valeurs expérimentales obtenues sont elles cohérentes avec le résultat théorique attendu?
![2
E[S2n|Si > 0, A i = 1,...,2n].
2n](nte19x.gif)
On simulera des marches aléatoires simples de longueur 2n sur 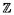 en ne conservant que celles restant
sur
en ne conservant que celles restant
sur 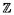 * + : on rejettera une trajectoire dès qu’elle passera par l’origine. Prendre garde au fait qu’il
est nécessaire de simuler un grand nombre de m.a. pour obtenir un nombre fixé MC de marches
“convenables”. On pourra imposer que le programme s’arrête si le nombre NBECH de marches rejetées
est supérieure à une certaine valeur MAX (débuter avec MAX=10000, par exemple, et augmenter cette
valeur si le temps de calcul est acceptable).
* + : on rejettera une trajectoire dès qu’elle passera par l’origine. Prendre garde au fait qu’il
est nécessaire de simuler un grand nombre de m.a. pour obtenir un nombre fixé MC de marches
“convenables”. On pourra imposer que le programme s’arrête si le nombre NBECH de marches rejetées
est supérieure à une certaine valeur MAX (débuter avec MAX=10000, par exemple, et augmenter cette
valeur si le temps de calcul est acceptable).
Essayer différentes valeurs de n (n = 1, ..., 5) et de MC (MC= 100, 1000,10000). Pouvez-vous estimer la valeur théorique?
![2 S22n-|
E[S2n|Si > 0, A i = 1,...,2n] =_ E[2n-1{Si>0, A i=1,...,2n}].
2n P[Si > 0, A i = 1,...,2n]](nte20x.gif)
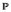 [Si>0,
[Si>0,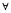 i=1,...,2n;S2n=x]= 1__
22n x _
2n C2n2n+x
2 , pour x
i=1,...,2n;S2n=x]= 1__
22n x _
2n C2n2n+x
2 , pour x 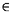 {2, 4, ..., 2n}.
{2, 4, ..., 2n}.
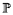 [Si > 0,
[Si > 0, 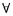 i = 1, ..., 2n] = 1 ___
22n+1 C2nn.
i = 1, ..., 2n] = 1 ___
22n+1 C2nn.Principe de réflexion : le nombre de trajectoires de longueur n sur 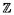 partant de a > 0, passant par 0, et
s’arrêtant en b > 0, est égal au nombre de trajectoires de longueur n partant de -a et s’arrêtant en
b.
partant de a > 0, passant par 0, et
s’arrêtant en b > 0, est égal au nombre de trajectoires de longueur n partant de -a et s’arrêtant en
b.
![(S2n)2 4 sum n 3 n+k
E[-2n--|Si > 0, A i = 1,...,2n] = n2Cn k C2n .
2nk=1](nte21x.gif)
![(S )2
E[--2n--|Si > 0, A i = 1,...,2n] = 2.
2n](nte22x.gif)
Une méthode : écrire
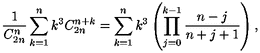
et montrer par récurrence sur p (p = 1, ..., n) que la somme des p derniers termes (k = n - p + 1, ..., n) vaut :