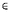
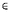
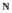 ,n
,n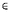
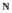 une famille de v.a.i.i.d. à valeurs entières positives. On construit une suite
(Zn )n
une famille de v.a.i.i.d. à valeurs entières positives. On construit une suite
(Zn )n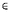
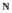 par :
par : 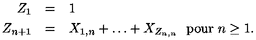
On se limitera ici à étudier des v.a. prenant les valeurs 0, 1 et 2.
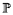 (X1,1 = i) et m =
(X1,1 = i) et m = 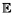 (X1,1), exprimez p1 et p2 en fonction de m et p0. Assurez-vous par
un test dans votre programme que le choix de m et p0 est permise. Écrire un programme donnant une
réalisation de la suite (Zn)1....,N avec m, p0 et N en entrées. Réfléchir aux débordements possibles
et imposer une limite supérieure MAXZ à Zn. (On rappelle que 231 - 1 = 2147483647).
(X1,1), exprimez p1 et p2 en fonction de m et p0. Assurez-vous par
un test dans votre programme que le choix de m et p0 est permise. Écrire un programme donnant une
réalisation de la suite (Zn)1....,N avec m, p0 et N en entrées. Réfléchir aux débordements possibles
et imposer une limite supérieure MAXZ à Zn. (On rappelle que 231 - 1 = 2147483647).
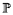 (Z
(Z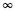 = 0). Pour cela réaliser une boucle
Monte-Carlo de MC réalisations de ZN et estimer
= 0). Pour cela réaliser une boucle
Monte-Carlo de MC réalisations de ZN et estimer 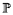 (ZN = 0). Introduire un compteur d’échecs
NBECH pour compter les cas où il y a débordement. Considérer différentes valeurs de p0 et m. (
p0 = 0, p0 > 0, m = 1, m > 1). Prendre N = 100, 1000, 10000. Qu’observez-vous?
(ZN = 0). Introduire un compteur d’échecs
NBECH pour compter les cas où il y a débordement. Considérer différentes valeurs de p0 et m. (
p0 = 0, p0 > 0, m = 1, m > 1). Prendre N = 100, 1000, 10000. Qu’observez-vous?
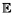 (ZN |ZN
(ZN |ZN 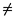 0) et comparer la avec mN . Quelle conjecture formulez vous?
0) et comparer la avec mN . Quelle conjecture formulez vous?L’animation en ligne donne un exemple de simulation des premières générations du processus.
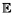 (tX) pour t élément de
[0, 1].
(tX) pour t élément de
[0, 1].
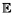 (tZn). Montrer que fn+1(t) = fn(f(t)) et que donc fn = fn (où le produit utilisé
est la composition des applications).
(tZn). Montrer que fn+1(t) = fn(f(t)) et que donc fn = fn (où le produit utilisé
est la composition des applications).
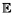 (Zn) et
(Zn) et 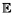 (Zn|Zn
(Zn|Zn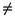 0).
0).