 |
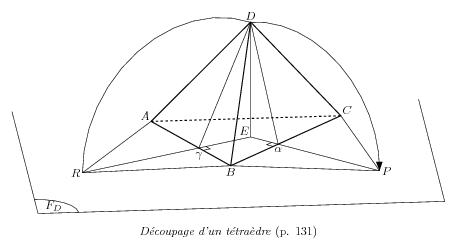
% Decoupage d'un tetraedre % 1. Definition des points caracteristiques de la geometrie \figinit{4cm,ortho} % Sommets \figpt 1:$D$(0.4,0.7,0.9) \figpt 2:$A$(0,0) \figpt 3:$B$(1,0.5) \figpt 4:$C$(0,1.4) % Plan de base (11,12,13,14) \figpt 11:(-0.3,-1)\figpttraC 12:$F_D$=11/2.2,0,0/ \figvectC 0(0,3)\figptstra 13=12,11/1,0/ % Points dans le plan de base \figvectC 10(0,0,1)% Vecteur orthogonal au plan de base \figptorthoprojplane 5:$E$=1/2,10/ \figptorthoprojline 6:$\gamma$=5/2,3/\figgetdist\Rcg[1,6] \figvectP 0[5,6]\figvectU 0[0]\figpttra 16:$R$=6/\Rcg,0/ \figptorthoprojline 7:$\alpha$=5/3,4/\figgetdist\Rca[1,7] \figvectP 0[5,7]\figvectU 0[0]\figpttra 17:$P$=7/\Rca,0/ % \figset proj(psi=-5,theta=20) % 2. Creation du fichier graphique \psbeginfig{} % Plan de base \psline[11,12,13,14] \psarccircP 12 ; 0.3 [13,11,11] % \def\DIM{0.06} \psline[1,5]\psline[1,6]\psline[1,7] \psaltitude \DIM[5,2,3]\psaltitude \DIM[5,4,3] \psline[6,16]\psline[2,16,3] \psline[7,17]\psline[3,17,4] \psarccircP 6;\Rcg[1,16,16] \psset arrow(fill=yes)\psarrowcircP 7;\Rca[1,17,17] % Aretes externes du tetraedre \psset(join=round,width=0.8)\psline[1,2,3,1,4,3] \psset(dash=4)\psline[2,4] \psendfig % 3. Inscription du texte sur le dessin \def\dist{2pt} \figvisu{\figBoxA}{\it D\'ecoupage d'un t\'etra\`edre \rm(p. 131)}{% \figwriten 1:(\dist)\figwritenw 2,5:(\dist) \figwrites 6:(3pt)\figwritene 4:(\dist) \figwrites 3,7:(\dist) \figwritew 16:(\dist)\figwritee 17:(\dist) \figwritege 12:(6pt,2pt) } \centerline{\box\figBoxA} |