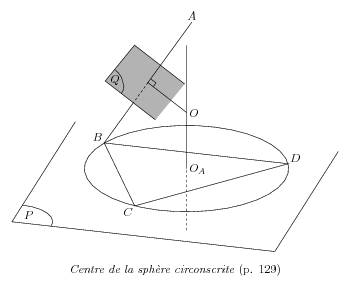
% Centre de la sphere circonscrite % 1. Definition des points caracteristiques de la geometrie \figinit{4cm,ortho} % Sommets \figpt 1:$A$(0.5,0.8,1.3) \figpt 2:$B$(0,0) \figpt 3:$C$(1,0.5) \figpt 4:$D$(0,1.4) \figptcircumcenter 5:$O_A$[2,3,4]\figgetdist\Rcc[2,5] % Plan de base (11,12,13,14) \figpt 11:(-0.3,-0.3)\figpt 12:$P$(1.5,-0.3) \figvectC 0(0,2)\figptstra 13=12,11/1,0/ \figvectC 10(0,0,1)% Vecteur orthogonal au plan de base % \figptbary 20:[1,2;1,1]% Milieu de [A,B] % Centre de la sphere circonscrite : 21 \figvectP 24[2,1]\figptinterlineplane 21 :$O$[5,10; 20,24] \figptrot 22:=21/20,90,24/ \figvectP 0[21,20]\figptstra 30=20,21,22/0.7,0/ \figvectP 0[22,20]\figptstra 30=30,31,32/0.7,0/ \figptstra 32=32/-0.3,0/ \figvectP 0[30,31]\figptstra 31=31/0.3,0/ \figvectP 0[30,32]\figptstra 33=31/1,0/ % \figset proj(psi=15,theta=25) % 2. Creation du fichier graphique \psbeginfig{} \figptvisilimSL 34:[ 30,31;1,2] % Plan mediateur \psset(color=0.7,fill=yes)\psline[33,32,30,31] \psset(color=\defaultcolor,fill=no) \psline[33,32,30,31]\psarccircP 30 ; 0.15 [31,32,32] % Aretes externes du tetraedre \psset(dash=4)\psline[20,34] \psset(dash=\defaultdash) \psline[2,3,4,2]\psline[34,2] \psaltitude 0.05[1,20,21]\psline[20,21] % Axe du cercle et cercle \figpttra 0:=5/1,10/\psline[0,5] \figpttra 0:=5/-0.5,10/\psset(dash=4)\psline[0,5]\psset(dash=\defaultdash) \pscirc 5,2,3(\Rcc) % Plan de base \psline[11,12,13,14] \psarccircP 12 ; 0.3 [13,11,11] \psendfig % 3. Inscription du texte sur le dessin \def\dist{2pt} \figvisu{\figBoxA}{\it Centre de la sph\`ere circonscrite \rm(p. 129)}{% \figwriten 1:(\dist)\figwritenw 2:(\dist) \figwritesw 3:(\dist)\figwritene 4:(\dist) \figwritee 5,21:(\dist) \figwritege 12:(10pt,2pt)\figwritegce 30:$Q$(4pt,1pt) } \centerline{\box\figBoxA}