 |
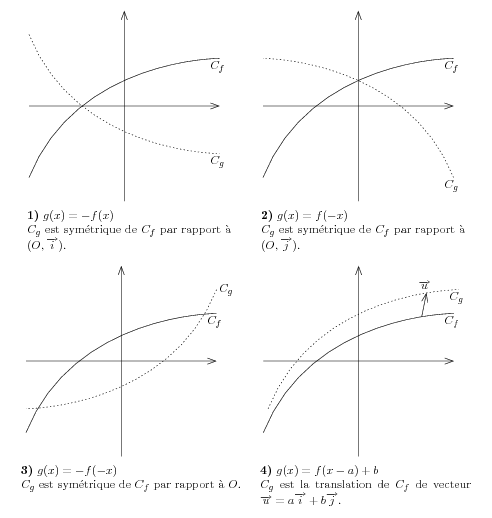
\input fig4tex.tex %%%%% %%% debut dessin %%%%%%%%%%%% %% definition des points \figinit{.7cm} % coordonnes donnees en cm % pt pour tracer les axes \figpt 1:(-4,0)\figpt 2:(4,0)\figpt 3:(0,-4)\figpt 4:(0,4) % pt pour tracer la courbe \figpt 10:(-4,-3) \figpt 11:(-2,2) \figpt 12:(4,2) \figpt 13:(4,2) %%%%%% %%% creation du fichier ps pour sym Ox %%%%%%% \figptssym 14=10,11,12,13/1,2/ \psbeginfig{} % dessin des axes \psarrow[1,2]\psarrow[3,4] % dessin de la courbe de base \psBezier 1[10,11,12,13] % dessin de la sym par rapport a Ox \pssetdash{5} \psBezier 1[14,15,16,17] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \newbox\symOx \figvisu{\symOx} {\vbox{\hsize=6cm {\bf 1)} $g(x)=-f(x)$\hfill\break $C_g$ est sym\'etrique de $C_f$ par rapport \`a $(O,\overrightarrow{i}).$}}{ \figwrites 13:$C_f$ (.1) \figwrites 16:$C_g$ (.1) } %%%%%%%%%%%% %%%%% creation du fichier du ps pour sym Oy \figptssym 14=10,11,12,13/3,4/ \psbeginfig{} % dessin des axes \psarrow[1,2]\psarrow[3,4] % dessin de la courbe de base \psBezier 1[10,11,12,13] % dessin de la sym par rapport a Ox \pssetdash{5} \psBezier 1[14,15,16,17] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \newbox\symOy \figvisu{\symOy}{\vbox{\hsize=6cm {\bf 2)} $g(x)=f(-x)$\hfill\break $C_g$ est sym\'etrique de $C_f$ par rapport \`a $(O,\overrightarrow{j}).$}}{ \figwrites 13:$C_f$ (.1) \figwrites 14:$C_g$ (.1) } %%%%%%%%%%%% %%%%% creation du fichier du ps pour sym O \figpt 0:(0,0) \figptshom 14=10,11,12,13/0,-1/ \psbeginfig{} % dessin des axes \psarrow[1,2]\psarrow[3,4] % dessin de la courbe de base \psBezier 1[10,11,12,13] % dessin de la sym par rapport a O \pssetdash{5} \psBezier 1[14,15,16,17] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \newbox\symO \figvisu{\symO}{\vbox{\hsize =6.5 cm{\bf 3)} $g(x)=-f(-x)$\hfill\break $C_g$ est sym\'etrique de $C_f$ par rapport \`a $O.$}}{ \figwrites 13:$C_f$ (.1) \figwritee 14:$C_g$ (.1) } %%%%%%%%%%%% %%%%% creation du fichier du ps pour trans \figvectC 0(.2,1) %% pt de depart du vecteur de translation \figptBezier 19::0.7[10,11,12,13] \figptstra 14=10,11,12,13,19/1,0/ \psbeginfig{} % dessin des axes \psarrow[1,2]\psarrow[3,4] % trace du vecteur de translation \psarrow[19,18] % dessin de la courbe de base \psBezier 1[10,11,12,13] % dessin de la sym par rapport a Ox \pssetdash{5} \psBezier 1[14,15,16,17] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \newbox\trans \figvisu{\trans}{\vbox{\hsize=6.2 cm {\bf 4)} $g(x)=f(x-a)+b$\hfill\break $C_g$ est la translation de $C_f$ de vecteur $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}.$}}{ \figwrites 13:$C_f$ (.1) \figwrites 17:$C_g$ (.1) \figwriten 18:$\overrightarrow{u}$ (.15) } %%%%%% \medskip %%%%%% \line{\hfill\box\symOx\hfill\hfill\box\symOy\hfill} \smallskip %%%%% \line{\hfill\vtop{\unvbox\symO}\hfill\hfill\vtop{\unvbox\trans}\hfill} %%%%%%% \bye |