 |
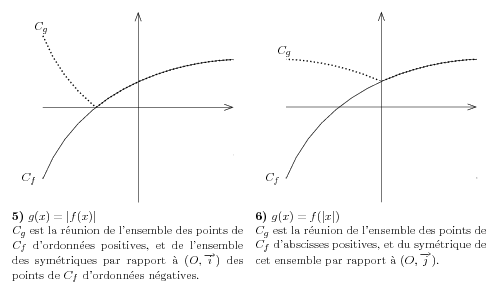
\input fig4tex.tex %%%%% %%% debut dessin %%%%%%%%%%%% %% definition des points \figinit{.7cm} % coordonnes donnees en cm % pt pour tracer les axes \figpt 1:(-4,0)\figpt 2:(4,0)\figpt 3:(0,-4)\figpt 4:(0,4) % pt pour tracer la courbe \figpt 10:(-4,-3) \figpt 11:(-2,2) \figpt 12:(4,2) \figpt 13:(4,2) %%%%%% %%%%%% %%% creation du fichier ps pour val absolue(f(x)) %%%%%%% \figptssym 14=10,11,12,13/1,2/ \psbeginfig{} % dessin de la courbe de base en pointille \pssetwidth{1}\pssetdash{5} \psBezier 1[10,11,12,13] % dessin de la sym par rapport a Ox \psBezier 1[14,15,16,17]\pssetwidth{\defaultwidth}\pssetdash{\defaultdash} % carre blanc pour cacher un bout de Cg et Cf \figpt 18:(-4,0)\figpt 19:(4,0)\figpt 20:(4,-4)\figpt 21:(-4,-4) \pssetfillmode{yes}\pssetgray{1} \psline[18,19,20,21,18] \pssetfillmode{no}\pssetgray{0} % dessin de la courbe de base en plein \psBezier 1[10,11,12,13] % dessin des axes \psarrow[1,2]\psarrow[3,4] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \figvisu{\figBoxA} {\vbox{\hsize=6.8 cm{\bf 5)} $g(x)=\vert f(x)\vert$\hfill\break $C_g$ est la r\'eunion de l'ensemble des points de $C_f$ d'ordonn\'ees positives, et de l'ensemble des sym\'etriques par rapport \`a $(O,\overrightarrow{i})$ des points de $C_f$ d'ordonn\'ees n\'egatives.}}{ \figwritew 10:$C_f$ (.1) \figwriten 14:$C_g$ (.1) } %%%%%%%%%%% %%%%% creation du fichier du ps pour f(val abso(x)) \figptssym 14=10,11,12,13/3,4/ \psbeginfig{} % dessin de la courbe de base en pointille \pssetwidth{1}\pssetdash{5} \psBezier 1[10,11,12,13] % dessin de la sym par rapport a Oy \psBezier 1[14,15,16,17]\pssetwidth{\defaultwidth}\pssetdash{\defaultdash} % carre blanc pour cacher un bout de Cg et Cf \figpt 18:(-4,1.1)\figpt 19:(4,1.1)\figpt 20:(-4,-4)\figpt 21:(4,-4) \pssetfillmode{yes}\pssetgray{1} \psline[18,19,21,20,18] \pssetfillmode{no}\pssetgray{0} % trace en plein de Cg \psBezier 1[10,11,12,13] % dessin des axes \psarrow[1,2]\psarrow[3,4] \psendfig % fin de la creation du fichier ps %%% ecriture sur le dessin \figvisu{\figBoxB}{\vbox to 2 cm{\hsize=6.8cm{\bf 6)} $g(x)=f(\vert x\vert)$\hfill\break $C_g$ est la r\'eunion de l'ensemble des points de $C_f$ d'abscisses positives, et du sym\'etrique de cet ensemble par rapport \`a $(O,\overrightarrow{j}).$}}{ \figwritew 10:$C_f$ (.1) \figwriten 17:$C_g$ (.1) } %%%%%% \medskip \line{\hfill\box\figBoxA\hfill\quad\hfill\box\figBoxB\hfill}\par %%%%%%% \bye |