WaterWaves1D.jl

A package for the numerical simulation of water waves models

Vincent Duchêne
Jun 27, 2022 5 min read

Together with P. Navaro, we have developped a Julia package: WaterWaves1D.jl. The aim of this package is to facilitate the comparison between the many existing models for the propagation of surface gravity waves (restricting to horizontal dimension $d=1$ and flat bottom).

Two big Ws with sinusoidal waves behind
Logo of the package

In particular, the package provides the necessary tools to solve numerically the initial-value problem1 for

  • the so-called water-waves system, based on the incompressible Euler equations, which can be thought as the “exact” equations for homogeneous and potential flows (notwithstanding, e.g., surface tension);
  • the Saint-Venant (or shallow water) system;
  • some $abcd$-Boussinesq systems;2
  • some Whitham–Boussinesq systems;3
  • the (Serre–)Green–Naghdi (or Su–Gardner) system;4
  • the Cotter–Holm–Percival “√D” system;5
  • the so-called “non-hydrostatic” system of Bristeau, Mangeney, Sainte-Marie and Seguin;6
  • the Whitham–Green–Naghdi system;7
  • the Isobe–Kakinuma model;8
  • the High Order Spectral model;9
  • the Matsuno system;10
  • the Akers–Nicholls system.11

It would be superfluous to describe here all these models. A short description can be found in the package documentation, and a more detailed account can be found in the book of Lannes12 or in my memoir13.

It is also not the place to describe the numerical method, relying on the fairly
standard (but extremely efficient in our idealized situation) Fourier-based pseudospectral methods, described for instance in this blog post.

Let me however mention that some of the models require some extra attention to fit in the framework of pseudospectral methods. Starting with the water-waves system, we follow the strategy advocated by Dyachenkoa, Kuznetsov, Spector and Zakharov14 using the power of conformal mapping (hence the strategy is inherently restricted to horizontal dimension $d=1$). Many of the models require to solve an elliptic problem before moving to the time-stepping step, which amounts to solve a large system of linear equations: this can be performed typically using a direct and readily available linear solver, or –in order to enhance performance– using the Krylov subspace iterative method GMRES.15

At the end of the day, we hope this package can be useful to quickly investigate properties of models (included in the above list or others, since adding a new model is made extremely easy) in comparison with other ones. This was already used by myself to

  1. produce beautiful pictures and movies in my Habilitation and memoir, Many Models for Water Waves;

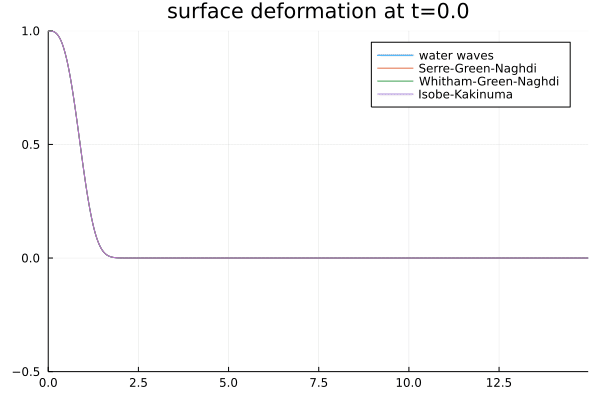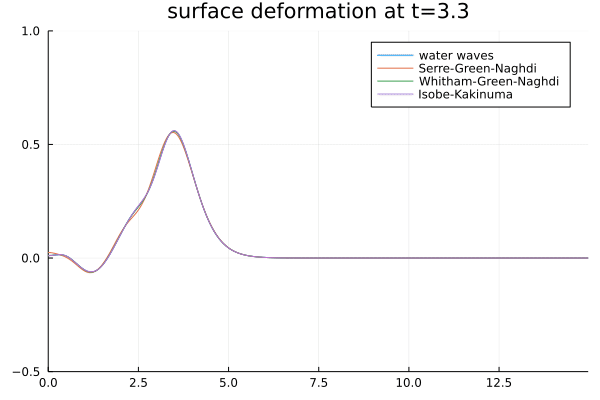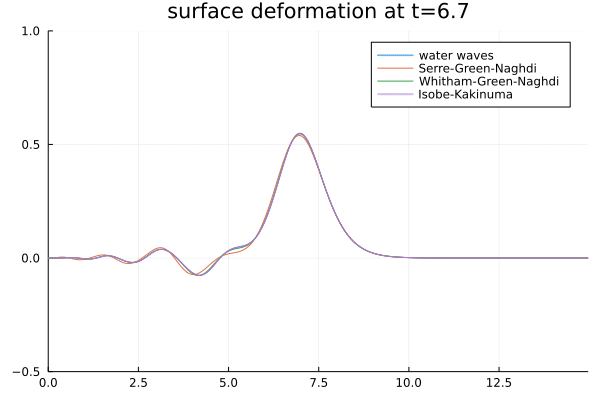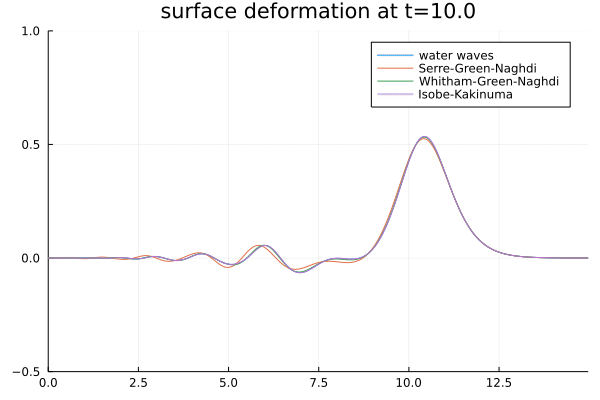
    A .gif showing the waves produced by the disintegration of a heap of water, according to the water waves, Green-Naghdi, and Isobe-Kakinuma models
    Disintegration of a heap of water, according to several models.

  2. investigate and compare the Green–Naghdi system and its fully dispersive counterpart (the Whitham–Green–Naghdi system), leading to a publication in collaboration with Christian Klein;16

    An image showing different curves representing data from an experiment, and predictions of three different models
    Fully dispersive models significantly improve the predictions of the Green-Naghdi model in the Hammack and Segur experiment.

  3. investigate deeply the high-frequency instabilities of the so-called “WW2” model (the first nonlinear system in the High Order Spectral hierarchy), leading to a publication (submitted) in collaboration with Benjamin Melinand.17

    Two images showing the result of a numerical simulation at three different times, both in physical and Fourier variables (the latter in log scale)
    The first system in the High Order Spectral model hierarchy exhibits high-frequency instabilities.

Please do not hesitate to contact me if you think this package can be helpful to you, as I would feel priviledged to discuss and offer services.

  1. The package also produces cnoidal and solitary waves for some of these systems. ↩︎

  2. J. L. Bona, M. Chen and J.-C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. I. Derivation and linear theory, J. Nonlinear Sci. 12(4):283–318, 2002 ↩︎

  3. see e.g. E. Dinvay, D. Dutykh and H. Kalisch, A comparative study of bi-directional Whitham systems, Appl. Numer. Math. 141:248–262, 2019 or L. Emerald, Rigorous derivation from the water waves equations of some full dispersion shallow water models, SIAM J. Math. Anal. 53 (4):3772–3800, 2021 ↩︎

  4. F. Serre, Contribution à l’étude des écoulements permanents et variables dans les canaux, La Houille Blanche, (6):830–872, 1953, C. H. Su and C. S. Gardner, Korteweg-de Vries equation and generalizations. III. Derivation of the Korteweg-de Vries equation and Burgers equation, J. Mathematical Phys., 10:536–539, 1969, and A. E. Green and P. M. Naghdi, A derivation of equations for wave propagation in water of variable depth, J. Fluid Mech., 78(02):237–246, 1976 ↩︎

  5. C. J. Cotter, D. D. Holm, and J. R. Percival, The square root depth wave equations, Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 466(2124):3621–3633, 2010 ↩︎

  6. M.-O. Bristeau, A. Mangeney, J. Sainte-Marie, and N. Seguin, An energy-consistent depth-averaged Euler system: derivation and properties, Discrete Contin. Dyn. Syst. Ser. B, 20(4):961–988, 2015 ↩︎

  7. V. Duchêne, S. Israwi, and R. Talhouk, A new class of two-layer Green-Naghdi systems with improved frequency dispersion, Stud. Appl. Math., 137(3):356–415, 2016 ↩︎

  8. M. Isobe, A proposal on a nonlinear gentle slope wave equation, Proc. Coast. Eng. Jpn. Soc. Civ. Eng., 41:1–5, 1994 [in Japanese] ↩︎

  9. D. G. Dommermuth and D. K. Yue, A high-order spectral method for the study of nonlinear gravity waves, J. Fluid Mech., 184:267–288, 1987, B. J. West, K. A. Brueckner, R. S. Janda, D. M. Milder, and R. L. Milton, A new numerical method for surface hydrodynamics, J. Geophys. Res., 92:11803–11824, 1987 and W. Craig and C. Sulem, Numerical simulation of gravity waves, J. Comput. Phys., 108(1):73–83, 1993 ↩︎

  10. Y. Matsuno, Nonlinear evolutions of surface gravity waves on fluid of finite depth, Phys. Rev. Lett. 69(4):609–611, 1992 ↩︎

  11. B. Akers and D. P. Nicholls, Traveling waves in deep water with gravity and surface tension, SIAM J. Appl. Math. 70(7), 2373–2389, 2010 (see also C. H. Arthur, R. Granero-Belinchón, S. Shkoller and J. Wilkening, Rigorous asymptotic models of water waves, Water Waves 1(1):71–130, 2019) ↩︎

  12. D. Lannes, The water waves problem, volume 188 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, 2013 ↩︎

  13. V. Duchêne, Many Models for Water Waves, AMS Open Math Notes:202109.111309, 2021 ↩︎

  14. A. I. Dyachenko, E. A. Kuznetsov, M. Spector, and V. E. Zakharov, Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping), Phys. Lett. A, 221(1-2):73–79, 1996 ↩︎

  15. Y. Saad and M. H. Schultz, GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems, SIAM J. Sci. Statist. Comput., 7(3):856–869, 1986 ↩︎

  16. V. Duchêne and C. Klein, Numerical study of the Serre-Green-Naghdi equations and a fully dispersive counterpart, Discrete Contin. Dyn. Syst. Ser. B. (2021) ↩︎

  17. V. Duchêne and B. Melinand, Rectification of a deep water model for surface gravity waves, arXiv preprint:2203.03277 ↩︎

Vincent Duchêne
Vincent Duchêne
Chargé de Recherche CNRS