Introduction à Metanet
Philippe Roux
9 janvier 2014
Ce document est une introduction à l’utilisation de Metanet, la boite à
outils de Scilab pour l’étude des graphes. Metanet ne fonctionne correctement
que jusqu’à la version 4.1.2 de Scilab, qui n’est aujourd’hui plus maintenue ni
disponible en téléchargement. Pour continuer à utiliser Metanet vous devez
vous tourner vers scicoslab, qui est totalement compatible avec la version 4
de Scilab.
Table des matières
1 L’éditeur de graphes metanet
Scicoslab possède une interface graphique spécialement dédiée à la manipulation
des graphes metanet. Nous allons voir comment l’utiliser pour construire un
graphe :
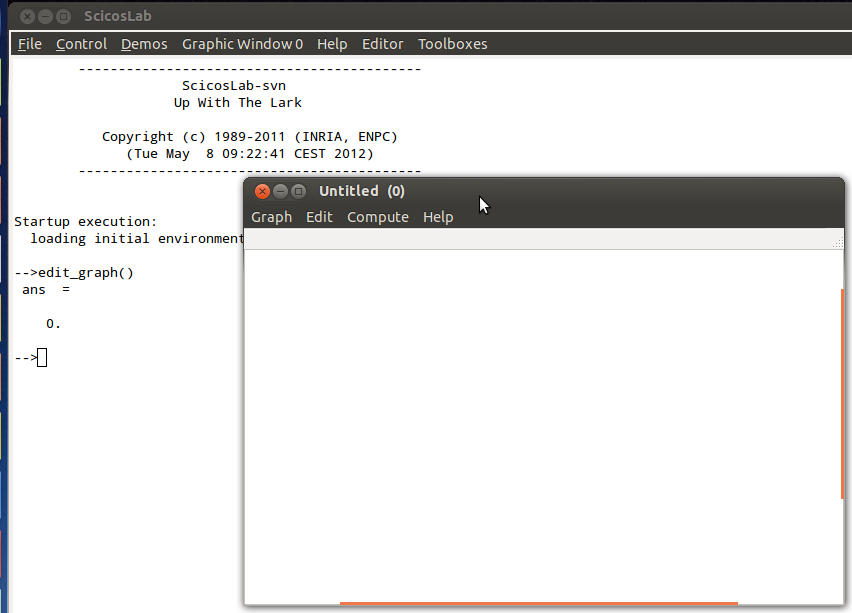
- Lancer l’éditeur de graphes avec la commande
une nouvelle fenêtre s’ouvre alors :
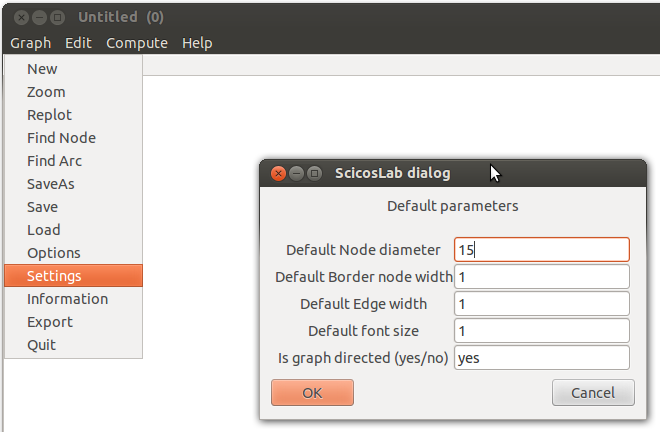
- Avant de commencer on peut avoir besoin de paramétrer le comportement de cette
fenêtre. Dans le menu graph de cette fenêtre choisir l’onglet settings permet
de paramétrer la taille des sommets et l’épaisseur des arcs qui seront
dessinés. Mais surtout le dernier paramètre “ is graph directed” permet de
définir le type de graphe qu’on va faire : orienté (yes) ou non-orienté
(no) :
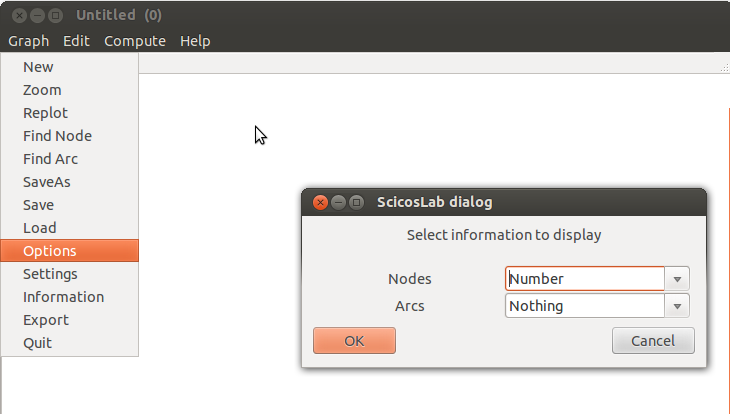
de même l’onglet options permet de choisir l’information qui sera indiquée à
proximité d’un sommet (node en anglais) ou d’un arc. Je vous conseille de choisir
pour le champ Nodes le paramètre number pour afficher automatiquement son
numéro à coté de chaque sommet :
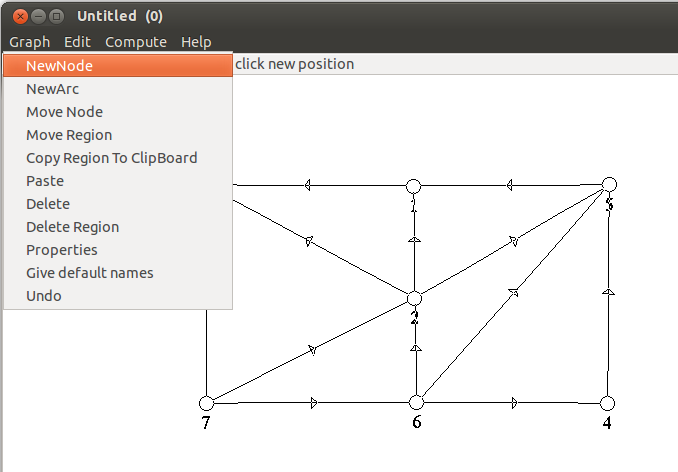
- Ensuite on peut commencer la construction du graphe. Pour cela nous allons
utiliser les fonctionnalités du menu edit. Pour créer les sommets choisir New Node,
à chaque clic gauche vous créez un nouveau sommet à l’endroit du clic le
numéro du nouveau sommet est incrémenté à chaque clic (et s’affiche si on
l’a spécifié via l’onglet options du menu graph). Pour créer les arcs
choisir New Arc, faire un clic gauche sur un sommet existant, pour définir
l’origine, puis un autre clic gauche sur un sommet existant, pour définir
l’extrémité de l’arc. L’arc s’affiche avec ou sans flèche suivant que le graphe
est orienté ou pas (cela a été spécifié via l’onglet settings du menu
graph).
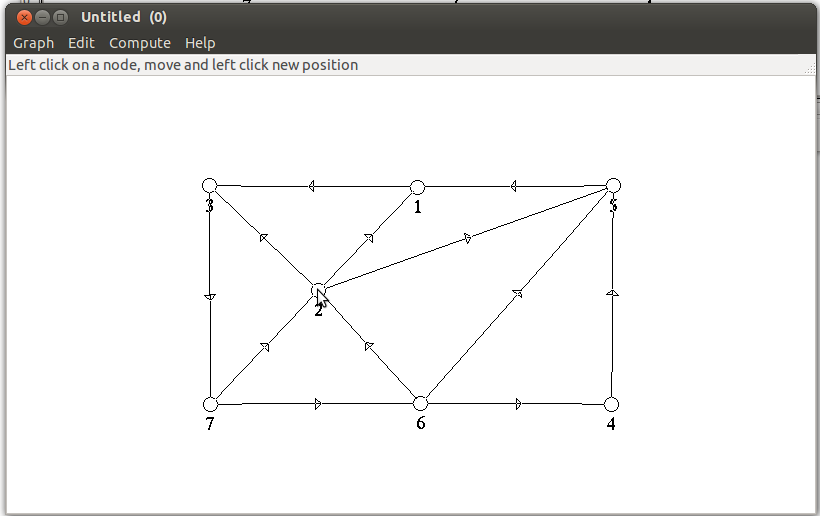
- Une fois le graphe saisi vous pouvez modifier la position des sommets pour que les
arcs ne cachent pas les informations affichées en utilisant la fonction
Move Node du menu edit. Faire un clic gauche sur un sommet puis le
déplacer avec la souris. Refaire un clic gauche à la nouvelle place désirée (le
sommets et les arcs qui y sont attachés se déplacent en même temps que la
souris).
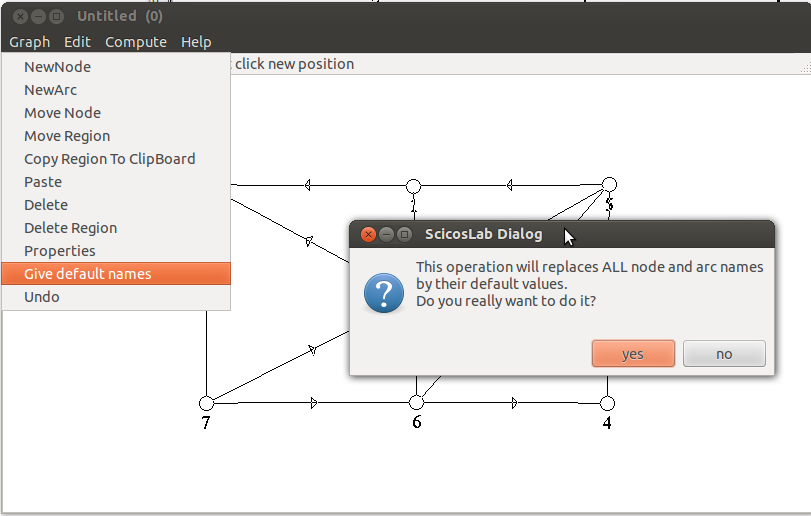
- Avant de pouvoir sauver le graphe, il faut indiquer à Scicoslab comment compléter
un grand nombre d’informations relatives au graphe (couleurs des arcs et sommets,
noms des sommets , etc. . .) en utilisant des valeurs par défaut. pour cela il faut
choisir Give default names dans l’onglet edit et cliquer sur yes dans la fenêtre
qui apparaît ensuite :
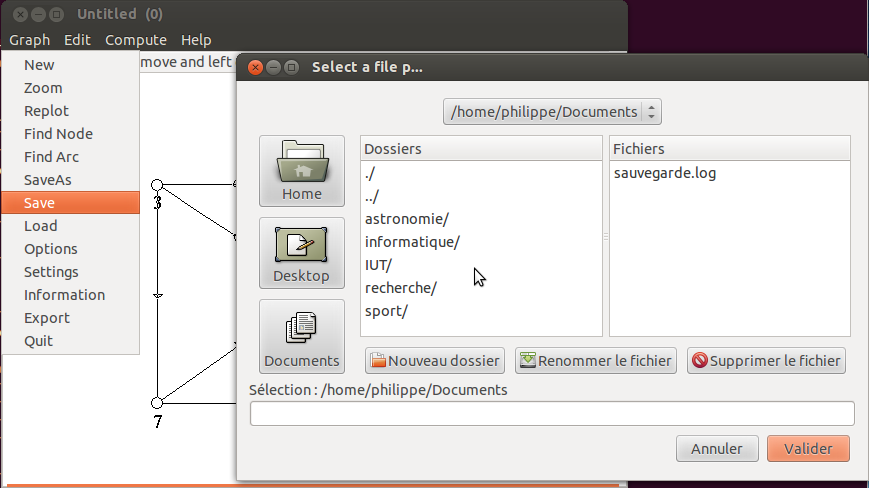
- Vous pouvez maintenant sauver le graphe en utilisant le menu SaveAs dans l’onglet
graph et choisir, dans la boite de dialogue qui apparaît, un nom de fichier avec
l’extension *.graph pour sauver le graphe :
Ce fichier sera créé dans le répertoire que vous choisirez (répertoire courant
par défaut) et contiendra toute la structure du graphe et va être utilisé
dans la console de Scicoslab pour effectuer divers calculs sur le graphe.
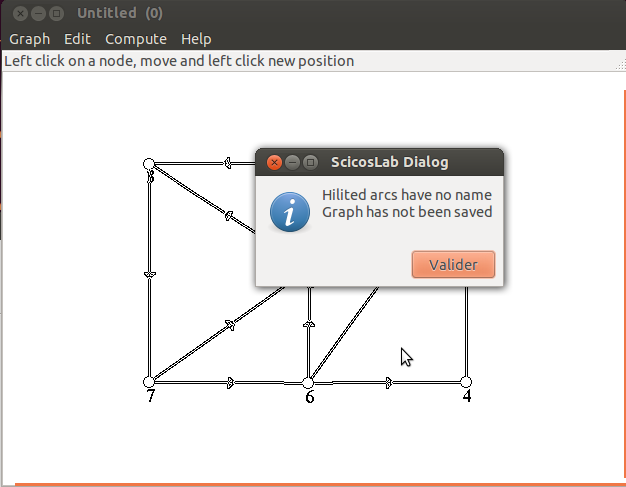
-
![[dangerous l bend]](manfnt-c-7f.png)
si vous n’avez pas cliqué sur le menu
Give default names à l’étape
précédente vous ne pourrez pas sauver le graphe et vous aurez le message d’erreur
suivant
:
2 Chargement d’un graphe dans Scicoslab
Nous venons de sauver la structure d’un graphe, créé avec metanet, dans un
fichier *.graph, inversement nous pouvons charger la structure d’un graphe dans
Scicoslab à partir de fichier *.graph. Pour charger le graphe, contenu dans le
fichier G.graph, dans l’environnement de travail il suffit maintenant d’appeler la
commande :
--> G=load_graph('G.graph') ;
La commande G= sert à stocker le contenu du fichier G.graph dans la
variable Scicoslab G (mais on aurait pu choisir tout autre nom de variable
valide
comme graphe ou monpremiergraphe . . .).
-
![[dangerous l bend]](manfnt-c-7f.png)
Pour que cela il faut que le fichier
*.graph se trouve dans le répertoire
courant de
Scicoslab , sinon vous aurez une erreur lors du chargement du graphe
:
-->G=load_graph('G.graph')
!--error 9999
Graph file "./G.graph" does not exist
at line 10 of function load_graph called by :
G=load_graph('G.graph')
-
![[dangerous l bend]](manfnt-c-7f.png)
si ce n’est pas le cas n’oubliez pas de changer ce répertoire avec la commande
cd par exemple
:
--> cd "Z :/Graphes/" //nouveau répertoire courant Z :/Graphes/
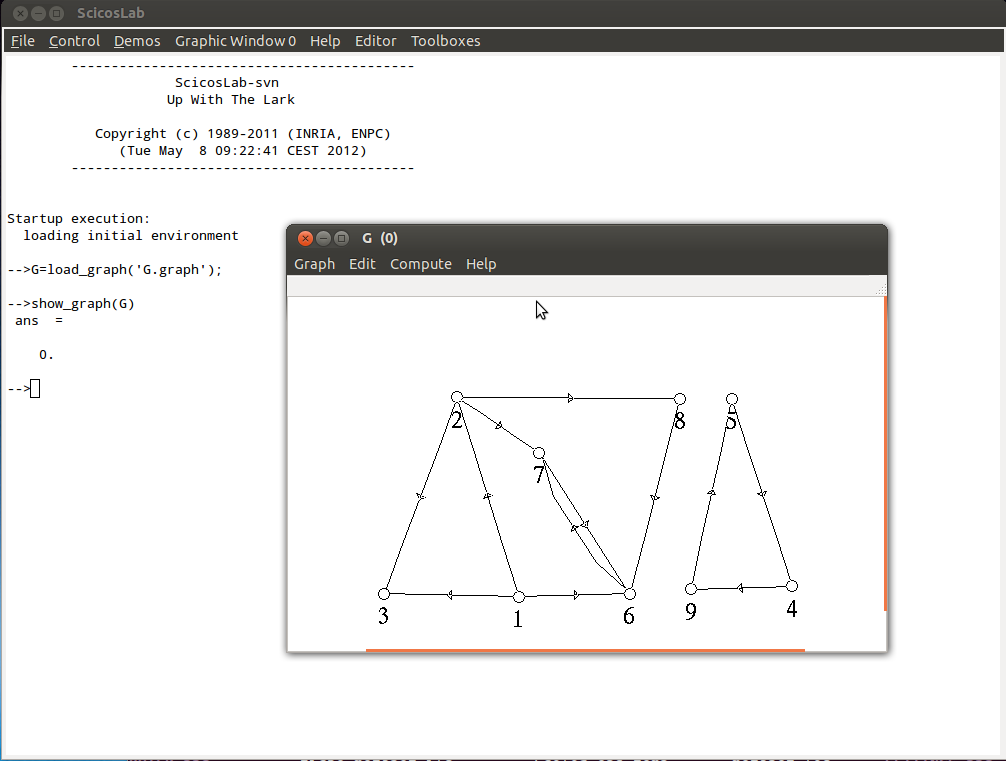
Maintenant que le graphe est chargé dans une variable vous pouvez le ré-afficher dans
metanet t avec la commande :
une nouvelle fenêtre de l’éditeur de graphes s’ouvre avec le graphe G dedans :
-
![[dangerous l bend]](manfnt-c-7f.png)
Attention, si l’éditeur de graphe n’a pas encore été ouvert (ou a été fermé)
il faut le reparamétrer (menu
options de l’onglet
graph) pour afficher les
informations relatives aux sommets et arcs.
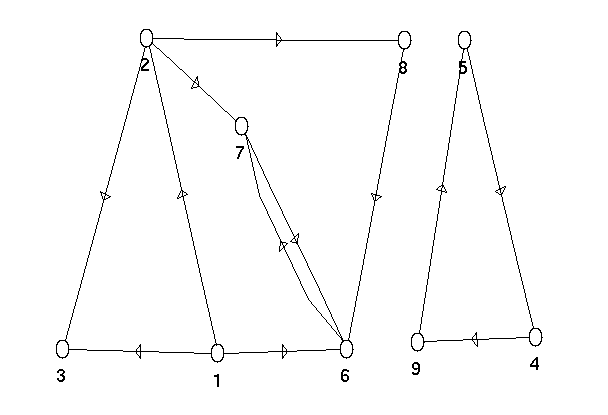
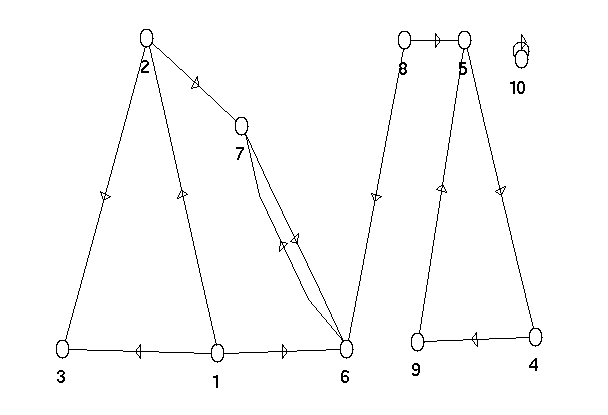
Au niveau de l’affichage des graphes on remarquera que :
- les numéros de sommets apparaissent sous le sommet,
- si le graphe est non-orienté les arêtes apparaissent comme de simples traits
rectilignes (sauf les boucles)
- si le graphe est orienté les arcs apparaissent sous forme de flèches droites,
sauf :
- les boucles (qui apparaissent comme un petit cercle)
- les “doubles flèches” (qui apparaissent sous forme de deux flèches séparées
légèrement courbées)
Il est possible d’utiliser plusieurs fenêtres graphiques différentes avec show_graph() en
ajoutant l’option ’new’. Il faudra alors faire attention à bien identifier la fenêtre
graphique par défaut lors des appels à show_graph. Pour contrôler cela on pourra utiliser
les fonctions netwindows() et netwindow() :
-->show_graph(G,'new')//affichage dans une nouvelle fenêtre
ans =
1.
-->netwindows()//liste des fenêtres graphiques + N° de la fenêtre par défaut
ans =
ans(1)
0. 1.
ans(2)
1.
-->netwindow(0)// choisir la fenêtre graphique 0 par défaut
-->netwindows()//nouvelle liste des fenêtres graphiques
ans =
ans(1)
0. 1.
ans(2)
0.
-->netclose(1)//ferme la fenêtre 1
-->netwindows()//nouvelle liste des fenêtres graphiques
ans =
ans(1)
0.
ans(2)
0.
Pour imprimer un graphe (vers un fichier PS, BMP, GIF, ou vers une imprimante) utiliser
le menu export du l’onglet graph.
3 Variable de type graph dans Scicoslab
La variable qui contient les information du graphe est d’un type particulier,
le type graph. Il s’agit d’une structure composée de 34 listes (des matrices à
1 ligne) d ?ailleurs si vous ne mettez pas le point virgule après la commande
G=load_graph(’G.graph’) ou si vous affichez G dans la console alors toutes ces
informations seront affichées à l’écran . . . et il y en a beaucoup et ce n’est pas très
lisible :
-->G=load_graph('G.graph') ; // chargement du graphe
-->typeof(G) // type de la variable G
ans =
graph
-->G // affichage des données du graphes
G =
G(1)
column 1 to 13
!graph name directed node_number tail head node_name node_type node_x node_y node_color node_diam node_border !
column 14 to 22
!node_font_size node_demand edge_name edge_color edge_width edge_hi_width edge_font_size edge_length edge_cost !
column 23 to 29
!edge_min_cap edge_max_cap edge_q_weight edge_q_orig edge_weight default_node_diam default_node_border !
column 30 to 34
!default_edge_width default_edge_hi_width default_font_size node_label edge_label !
G(2)
G
G(3)
1.
G(4)
9.
G(5)
1. 1. 1. 2. 2. 2. 7. 6. 4. 5. 9. 8.
[More (y or n) ?]
Ces 34 listes contiennent les propriétés du graphes, nous aurons besoin d’y accéder
pour effectuer certains traitements sur les graphes. Pour un graphe stocké dans la variable
G, chaque propriété du graphes est accessibles de 3 manières :
- G(i) où i est le numéro de la propriété
- G.prop où prop est le nom de la propriété
- G(’prop’) où prop est le nom de la propriété
-
![[dangerous l bend]](manfnt-c-7f.png)
On utilisera le plus souvent deuxième syntaxe
G.prop. Voici la liste
exhaustive que l’on peut aussi obtenir dans l’aide en ligne
:
La description de toutes ces listes se trouve dans l’aide en ligne de Scicoslab :
en voici un bref récapitulatif :
|
|
|
|
n∘ | Nom | type | description
|
|
|
|
|
| |
| | | | |
|
|
|
|
| 1 | graph | string |
vecteur ligne avec le nom du type graph
puis les noms des propriétés 2 à 34 |
|
|
|
|
| 2 | name | string |
le nom du graphe. C’est une chaîne de
caractères (longueur < 80). |
|
|
|
|
| 3 | directed | constant |
flag donnant le type du graphe. Il est
égal à 1 (graphe orienté) ou égal à 0
(graphe non-orienté). |
|
|
|
|
| 4 | node_number | constant |
nombre de sommets |
|
|
|
|
| 5 | tail | constant |
vecteur ligne des numéros des sommets
origines |
|
|
|
|
| 6 | head | constant |
vecteur ligne des numéros des sommets
extrémités |
|
|
|
|
| 7 | node_name | string |
vecteur ligne des noms des sommets.
Les noms des sommets doivent être
différents. Par défaut les noms des
sommets sont égaux à leurs numéros. |
|
|
|
|
| 8 | node_type | constant |
vecteur ligne des types des sommets. Le
type est un entier entre 0 et 2, 0 par
défaut : 0 = sommet normal , 1= puits,
2= source |
|
|
|
|
| 9 | node_x | constant |
vecteur ligne des coordonnées x des
sommets. Valeur par défaut calculée. |
|
|
|
|
| 10 | node_y | constant |
vecteur ligne des coordonnées y des
sommets. Valeur par défaut calculée. |
|
|
|
|
| 11 | node_color | constant |
vecteur ligne des couleurs des sommets,
des entiers correspondants a la table de
couleur courante. |
|
|
|
|
| 12 | node_diam | constant |
vecteur ligne
des diamètres des sommets en pixels,
un sommet est dessiné sous forme d’un
cercle. Par défaut, valeur de l’élément
default_node_diam . |
|
|
|
|
| 13 | node_border | constant |
vecteur ligne
de l’épaisseur des bords des sommets.
un sommet est dessiné sous forme d’un
cercle, par défaut, valeur de l’élément
default_node_border . |
|
|
|
|
| 14 | node_font_size | constant |
vecteur ligne de la taille de la police
utilisée pour afficher le nom du
sommet. Les tailles possibles sont : 8,
10, 12, 14, 18 ou 24. Par défaut, valeur
de l’élément default_font_size . |
|
|
|
|
| 15 | node_demand | constant |
vecteur ligne des demandes des
sommets, 0 par défaut ; |
|
|
|
|
| 16 | edge_name | string |
vecteur ligne des noms d’arêtes. Il est
souhaitable que les noms des arêtes
soient différents, mais c’est n’est pas
obligatoire. Par défaut les noms des
arêtes sont leur numéros. |
|
|
|
|
| 17 | edge_color | constant |
vecteur ligne des couleurs des arêtes.
des entiers correspondants a la table de
couleur courante. |
|
|
|
|
| 18 | edge_width | constant |
vecteur ligne des épaisseurs des arêtes
en pixels, par défaut, valeur de
l’élément default_edge_width . |
|
|
|
|
| 19 | edge_hi_width | constant |
vecteur ligne des épaisseurs des arêtes
mises en évidence (en
pixels), par défaut, valeur de l’élément
default_edge_hi_width . |
|
|
|
|
| 20 | edge_font_size | constant |
vecteur ligne de la taille de la police
utilisée pour afficher le nom des arêtes.
Les tailles possibles sont : 8, 10, 12,
14, 18 ou 24. Par défaut, valeur de
l’élément default_font_size . |
| |
|
|
|
|
| 21 | edge_length | constant |
vecteur ligne des longueurs des arêtes,
0 par défaut. |
|
|
|
|
| 22 | edge_cost | constant |
vecteur ligne des coûts des arêtes, 0 par
défaut. |
|
|
|
|
| 23 | edge_min_cap | constant |
vecteur ligne des capacités minimum
des arêtes, 0 par défaut. |
|
|
|
|
| 24 | edge_max_cap | constant |
vecteur ligne des capacités maximum
des arêtes, 0 par défaut. |
|
|
|
|
| 25 | edge_q_weight | constant |
vecteur ligne des poids quadratiques
des arêtes, 0 par défaut. |
|
|
|
|
| 26 | edge_q_orig | constant |
vecteur ligne des origines quadratiques
des arêtes, 0 par défaut. |
|
|
|
|
| 27 | edge_weight | constant |
vecteur ligne des poids des arêtes, 0 par
défaut. |
|
|
|
|
| 28 | default_node_diam | constant |
diamètre par défaut des sommets du
graphe, 20 pixels par défaut. |
|
|
|
|
| 29 | default_node_border | constant |
épaisseur du bord des sommets, 2 pixels
par défaut. |
|
|
|
|
| 30 | default_edge_width | constant |
épaisseur par défaut des arêtes du
graphe,1 pixel par défaut. |
|
|
|
|
| 31 | default_edge_hi_width | constant |
taille par défaut des arêtes mises
en évidence (en pixels), 3 pixels par
défaut. |
|
|
|
|
| 32 | default_font_size | constant |
taille par défaut de la police utilisée
pour afficher le nom des sommets et
arêtes. 12 par défaut |
|
|
|
|
| 33 | node_label | string |
vecteur ligne des noms des sommets |
|
|
|
|
| 34 | edge_label | string |
vecteur ligne des noms des arêtes |
|
|
|
|
| |
| |
| |
| |
| |
|
|
|
|
|
|
Les propriétés du graphe sont donc des matrices de réels (constant) ou de chaînes de
caractères (string), à défaut de toutes les retenir on pourra se souvenir qu’elles se
regroupent en 6 grandes catégories :
- la propriété 1 contient le nom du type graph puis les noms des propriétés 2
à 34,
- les propriétés 2 à 6 comportent les informations minimales pour créer un graphe,
son nom,son type,le nombre de sommets, et les arcs sous forme de deux matrices
G.tail et G.head à 1 ligne et m colonnes contenant les extrémités de chaque
arc :
-->G.directed // graphe orienté
ans =
1.
-->G.node_number // nombre de sommets
ans =
9.
-->[G.head ;G.tail] // liste des arcs
ans =
2. 3. 6. 7. 3. 8. 6. 7. 9. 4. 5. 6.
1. 1. 1. 2. 2. 2. 7. 6. 4. 5. 9. 8.
- les propriétés 7 à 15 sont des vecteurs à 1 ligne et n colonnes décrivant les
caractéristique de chaque sommet et dénommés node_*, par exemple
G.node_color contient les couleurs des sommets :
-->n=G.node_number//nombre de sommets
n =
9.
-->G.node_color// les couleurs des n sommets
ans =
1. 1. 1. 1. 1. 1. 1. 1. 1.
-->G.node_color=[3 4 5 2 3 4 5 2 3] ;//on modifie les couleurs
-->G.node_color// nouvelles couleurs des sommets
ans =
3. 4. 5. 2. 3. 4. 5. 2. 3.
- les propriétés 16 à 27 sont des matrices à 1 ligne et m colonnes décrivant les
caractéristique de chaque arc et dénommés edge_*, par exemple G.edge_color
contient les couleurs des arcs/arêtes :
-->G.edge_color//les couleurs des arcs
ans =
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
-->G.edge_color=5*ones(G.edge_color) ;//couleurs des arcs à 5(=rouge)
-->G.edge_color//nouvelles couleurs des arcs
ans =
5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5.
-->G.default_node_border=5 ;//grossir la taille des sommets
-->show_graph(G) ;
- les propriétés 28 à 32 dénommées default_* sont des réels donnant certaines
valeurs par défaut du graphe, ces valeurs qui peuvent se substituer aux valeurs
indiquées par certaines propriétés node_* ou edge_* le cas échéant. par
exemple pour changer la taille par défaut de l’épaisseur du bord d’un
sommet :
-->G.node_border // épaisseur du bord de chaque sommet
ans =
0. 0. 0. 0. 0. 0. 0. 0. 0.
-->G.default_node_border // épaisseur par default
ans =
1.
-->G.default_node_border=5 ;//grossir l'épaisseur du bord des sommets
- les propriétés 33 et 34, dénommées *_label, peuvent contenir, temporairement,
une liste de chaînes de caractères associées aux sommets et aux arcs. Cela peut
être pratique pour afficher certaines valeurs dans la fenêtre graphique de metanet
(par exemple afficher 2 propriétés sur chaque arc) mais ces valeurs ne peuvent pas
être sauvées dans le fichier *.graph !
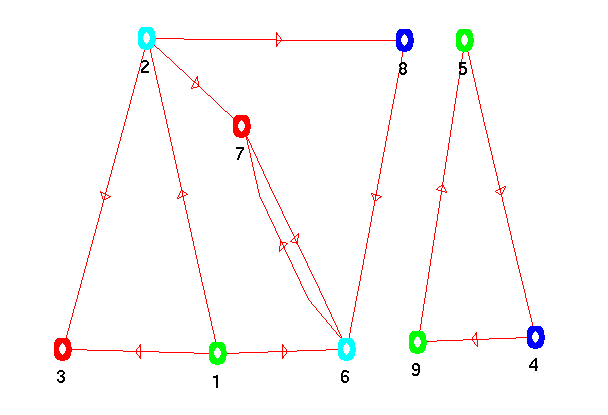
La modification des propriétés de G modifierons l’affichage du graphe lors du prochain appel
de show_graph(G) :
La table des couleurs par défaut de Scicoslab est la suivante (utiliser getcolor()) :
|
|
|
|
|
|
|
|
|
|
|
|
| numéro | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | . . . |
|
|
|
|
|
|
|
|
|
|
|
|
| couleur | noir | bleu | vert | cyan | rouge | magenta | rouge | blanc | . . . |
|
|
|
|
|
|
|
|
|
|
|
|
| |
-
![[dangerous l bend]](manfnt-c-7f.png)
On ne peut afficher un graphe
G que s’il possède des coordonnées pour ses
sommets c’est à dire si les propriétés
G.node_x et
G.node_y ne sont pas vides
sinon on aura une erreur
:
-->G.node_x
ans =
151. 69. - 28. 516. 435. 299. 178. 366. 381.
-->G.node_y
ans =
52. 318. 56. 66. 316. 56. 244. 316. 62.
-->G.node_x=[] ;G.node_y=[] ; // on efface les coordonnées des sommets
-->show_graph(G)
!--error 15
submatrix incorrectly defined
at line 31 of function ge_draw_loop_arcs called by :
at line 20 of function ge_drawarcs called by :
at line 10 of function ge_drawobjs called by :
at line 94 of function edit_graph called by :
at line 41 of function show_graph called by :
show_graph(G)
4 Principales fonctions pour les graphes
Nous allons maintenant examiner les différentes actions de base qu’on peut faire sur un
graphe avec Scicoslab . Ces actions de base peuvent être faites directement sur
les propriétés de la variable G, mais pour simplifier leur utilisation elles sont
aussi codées sous forme de fonctions. Reprenons le dernier graphe de la partie
précédente :
-->G=load_graph('G.graph') ;//chargement du graphe
-->show_graph(G) ;//affichage du graphe
On peut récupérer le nombre de sommets soit directement dans le graphe (avec la
propriété G.node_number soit avec la fonction node_number(G)
-->G.node_number//lecture du nombre de sommets dans le graphe
ans =
9.
-->node_number(G)//fonction équivalente
ans =
9.
De même on peut récupérer le nombre d’arcs directement dans le graphe en calculant la
longueur des listes G.tail et G.head ou en utilisant une fonction edge_number(G) ou
arc_number(G) (suivant que le graphe est orienté ou pas) :
-->length(G.tail)//=calcul du nombre d'arêtes ou d'arcs
ans =
12.
-->arc_number(G)//=nombre d'arcs d'un graphe orienté
ans =
12.
-->edge_number(G)//=nombre d'arêtes pour un graphe non-orienté
ans =
12.
-
![[dangerous l bend]](manfnt-c-7f.png)
pour un graphe non-orienté
arc_number(G) renvoie 2 fois le nombre d’arêtes
!
Ensuite il existe plusieurs fonctions pour rechercher les prédécesseurs, successeurs ou
les voisins d’un sommet :
-->arcs=[G.head ;G.tail]//liste des arcs
arcs =
2. 3. 6. 7. 3. 8. 6. 7. 9. 4. 5. 6.
1. 1. 1. 2. 2. 2. 7. 6. 4. 5. 9. 8.
-->predecessors(2,G)//prédécesseurs de 2
ans =
1.
-->successors(2,G)//successeurs de 2
ans =
7. 3. 8.
-->neighbors(2,G)//voisins de 2
ans =
1. 3. 7. 8.
-
![[dangerous l bend]](manfnt-c-7f.png)
On évitera d’utiliser les fonctions
predecessors et
successors pour un
graphe non-orienté (ou ces notions ne sont pas définies), mais on utilisera plutôt
dans ce cas la fonction
neighbors. Par contre pour un graphe orienté
neighbors
renvoie bien la liste des prédécesseurs et des successeurs.
On peut aussi modifier la structure du graphe en enlevant/ajoutant des arcs
ou des sommets avec les fonctions delete_nodes, delete_arcs, add_node et
add_edge :
-->G=delete_arcs([2,8],G) ;//détruire un arc
-->G=add_edge(8,5,G) ;//ajouter un arc
-->n=node_number(G) ;//nombre de sommets
-->G=add_node(G,[500,300]) ;//ajouter un sommet
-->G=add_edge(n+1,n+1,G) ;//ajouter une boucle
-->show_graph(G)
-
![[dangerous l bend]](manfnt-c-7f.png)
La commande
G1=delete_nodes(x,G) créée un nouveau graphe
G1
correspondant au graphe
G duquel on a enlevé le sommet
x (et tous les arcs qui
lui sont adjacents). Mais attention, dans
G1 la numérotation des sommets a changé,
les numéros de sommets plus grand que
x ont subi un
≪ décalage à gauche
≫(
i.e.
ces numéros ont diminué de 1). Par contre le ”nom” de ces sommets (propriété
node_name) n’a pas changé
!
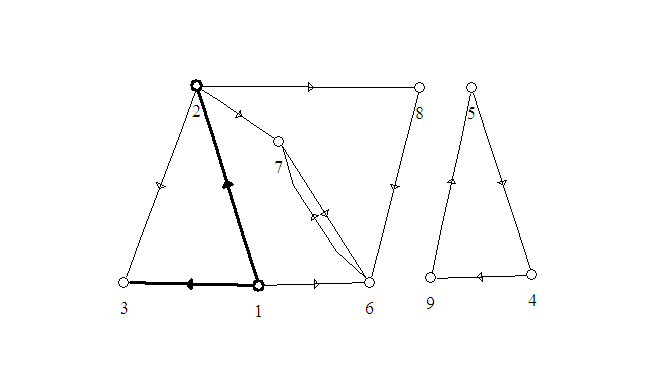
On a enfin des fonctions qui permettent de mettre en évidence (en gras) des sommets
ou des arcs :
-->G=load_graph('G.graph') ;//chargement du graphe
-->show_graph(G) ;//affichage du graphe
-->show_arcs([1,2])//met en gras les arcs 1 et 2
-->show_nodes([1,2],'sup') //met en gras les sommets 1 et 2
-
![[dangerous l bend]](manfnt-c-7f.png)
Dans beaucoup de cas (comme pour
show_arcs) il faut comprendre que
chaque arcs est numéroté par l’ordre dans le quel ses extrémités apparaissent
dans les listes
tail et
head ! Ici on peut vérifier que les arcs numérotés 1 et 2 sont
bien les arcs (1
, 2) et (1
, 3)
:
-->arcs=[G.head ;G.tail]//liste des arcs
arcs =
2. 3. 6. 7. 3. 8. 6. 7. 9. 4. 5. 6.
1. 1. 1. 2. 2. 2. 7. 6. 4. 5. 9. 8.
Pour finir on peut créer un graphe à partir d’une liste d’arcs (deux listes tail et head)
avec la commande G = make_graph('G',oriente,n,tail,head) mais il ne contient pas
de coordonnées de sommets donc ne peut être affiché directement ! La fonction
G = gen_net() permet de générer un graphe planaire aléatoire (avec informations
graphiques) l’intérêt de cette fonction est qu’elle détermine la position des sommets
de telle sorte que les arcs ne se croisent pas. C’est un avantage pour générer
facilement des exemples de graphes lisibles (malgré un bug mineur dans cette
fonction)
5 Exercices
Pour finir quelques petits exercices pour comprendre comment fonctionnent les fonctions
de base sur les graphes.
-
P
Ex. 1 Soit G un graphe simple orienté. Écrire les fonctions Scicoslab suivantes,
sans utiliser les fonctions predecessors, successors, neighbors, mais en accédant
directement aux propriétés du graphe G :
- L=predecesseurs(x,G) liste des prédécesseurs de x dans G
- L=successeurs(x,G) liste des successeurs de x dans G
- L=voisins(x,G) liste des voisins de x dans G
solution : l’idée est de parcourir la liste des arcs (s,t) et quand l’un des sommets est
égal à x l’autre est un prédécesseurs ou un successeur de x. Ensuite il y a de nombreuses
manières de mettre en œuvre cette stratégie soit en utilisant des boucles (for ou while)
soit en utilisant la fonction de recherche find.
-
P
Ex. 2 Soit G un graphe simple, orienté ou non, et écrire une fonctions
Scicoslab k=arc_2_num(x,y,G) qui calcule la liste des numéros k(i) de chacun des
arcs (x(i),y(i)) si ils existent, ou k = [] sinon.
solution : la difficulté ici est double, il faut traiter plusieurs arcs dans la même
fonction et traiter à la fois les graphes orientés et non-orientés.
-
P
Ex. 3 À
partir de la fonction gen_net() créer une fonction gen_graph(n,directed) qui
génère aléatoirement un graphe à n sommets orienté si n = 1 et non-orienté sinon.
![[dangerous l bend]](manfnt-c-7f.png) si vous n’avez pas cliqué sur le menu Give default names à l’étape
précédente vous ne pourrez pas sauver le graphe et vous aurez le message d’erreur
suivant :
si vous n’avez pas cliqué sur le menu Give default names à l’étape
précédente vous ne pourrez pas sauver le graphe et vous aurez le message d’erreur
suivant :