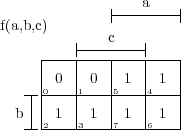
Dessiner le tableau de karnaugh d’une fonction booléenne à 4 ou 5 variables à l’aide d’un traitement de texte n’est pas chose aisée. Cependant, pour les utilisateurs de LATEX, il existe un package qui permet de simplifier l’écriture de tels tableau, le package kvmacros de A.W. Wieland.
En fait il s’agit d’un simple fichier kvmacros.tex contenant un ensemble de
commandes pour produire des tableaux de Karnaugh respectant les conventions les
plus usitées. Il suffit de mettre dans le préambule du document \input
kvmacros pour pouvoir utiliser ces commandes. Ensuite pour insérer un tableau
de Karnaugh il faudra appeler la commande karnaughmap avec la syntaxe
suivante :
\karnaughmap{nbre_var}{nom_fonc}{var}{val}{commandes graphiques}
Quelques remarques à propos des différents paramètres :
Prenons un exemple, pour obtenir le tableau de Karnaugh suivant :
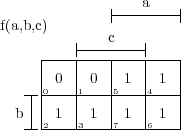
on a utilisé la commande :
\karnaughmap{3}{f(a,b,c)}{abc}{00111111}{}
|
On peut personnaliser l’affichage du tableau à partir des commandes :
En reprenant l’exemple précédent :
\kvnoindex
\kvunitlength=12mm \karnaughmap{3}{f(a,b,c)}{abc}{~~111111}{} |
on obtient :
Il ne reste donc plus qu’à placer les groupements sur le tableau de Karnaugh en utilisant les capacités graphiques de LATEX. Voici quelques exemples de commandes très simples à lire :
\put(x_pos,y_pos){object(x_dim,y_dim)}
|
Par exemple pour entourer le groupement 
dans ce tableau
il a suffit de placer un oval rouge centré sur les coordonnées x_pos=1 et y_pos=1.5, de
largeur un peu inférieure à 2 (1.8 ici) et de longueur un peu inférieure à 1 (0.8 ici), et
de placer le texte 
à coté (en position (2.2,1.5) ) :
\kvnoindex
\kvunitlength=12mm \karnaughmap{2}{$f(a,b)$}{{$a$}{$b$}}{11~~} { \put(1,1.5){\color{red}\oval(1.8,0.8)} \put(2.2,1.5){\color{red}$\bar a$} } |
Si on trouve que l’ordre des variables n’est pas « naturel »on peut le modifier mais cela influe sur la position des groupements :
|
Ces packages permettent donc de créer facilement des tableaux de Karnaugh …sauf qu’il est vite assez pénible de faire la liste des valeurs de la fonction dans l’ordre des monômes canoniques ou de rentrer manuellement toutes les informations sur les groupements (sans compter les erreurs de saisie). C’est pour cette raison que j’ai écrit quelques fonctions Scilab pour automatiser ce travail! Je vais décrire ci-dessous les principales fonctions contenues dans le fichier Karnaugh.sce qui permettent de résoudre ces problèmes. Le code est loin d’être optimal, mais il marche et il est suffisamment commenté pour donner des idées au lecteur intéressé.
Il faut d’abord fixer quelques conventions d’écriture pour représenter les expressions booléennes. L’idée est de représenter une fonction :
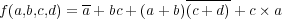
_a+bc+(a+b)_(c+d)+c*a
on considérera donc que :
Scilab permet de faire du calcul booléen avec la syntaxe suivante :
Maintenant pour pouvoir manipuler les fonctions booléennes avec scilab, il faut construire une fonction qui permette de traduire la chaîne de caractères :
_a+bc+(a+b)_(c+d)+c*a
en une expression booléenne scilab :
(~a)|(b&c)|(((a)|(b))&~((c)|(d)))|(c&a)
C’est ce qui est réalisé par la fonction boolean_2_scilab qui prend en entrée une chaîne de caractère représentant une expression booléenne et renvoie en sortie une autre chaîne de caractères représentant la traduction de cette expression booléenne en langage scilab. Cette fonction ne se contente pas de remplacer les + par | ou * par &, elle doit surtout gérer les problèmes de parenthésage liés aux conventions de priorités entre les opérateurs + et * énoncées plus haut.
Une fois la fonction booléenne traduite en expression scilab, il faut pouvoir évaluer cette fonction afin de remplir son tableau de Karnaugh. Si on a la liste des variables a,b,c …et l’expression booléenne de la fonction sous forme de chaînes de caractères var et expr_scilab il est facile de créer la fonction scilab associée via la commande :
deff(’bool=f(’+var’)’,’bool=’+expr_scilab)
|
il faut ensuite évaluer f pour tous les choix de valeurs possibles pour les variables a,b,c …Pour n variables il y a 2n possibilités, qui correspondent à l’écriture binaire des nombres de 0 à 2n-1. J’ai donc écrit une fonctions [E]=binaire(e,w) qui écrit dans un tableau E l’entier e sous forme binaire avec w bits, mais avec %t à la place de 1 et %f à la place de 0. Ensuite la fonction calcule_tab_karnaugh crée la fonction booléenne et appelle autant de fois que nécessaire la fonction binaire pour remplir le tableau de Karnaugh :
-->vars=[’a’ ’b’ ’c’ ’d’]//ordre par défaut des variables
vars = !a b c d ! -->expr_scilab=’~(a&d&(~c))’ expr_scilab = ~(a&d&(~c)) -->calcule_tab_karnaugh(vars,expr_scilab) ans = 111111111~111~11 -->vars=[’a’ ’c’ ’b’ ’d’]//on change l’ordre des variables vars = !a c b d ! -->calcule_tab_karnaugh(vars,expr_scilab) ans = 111111111~1~1111 |
les résultats précédents permettent de construire les tableaux de Karnaugh :
|
\karnaughmap{4}{}{abcd}{111111111~111~11}{}
|
On peut enfin écrire une fonction qui génére l’ensemble du code LATEX relatif au tableau de Karnaugh :
-->[latex]=tab_karnaugh(’f’,’ab+_c(d+_a)’,vars)
latex = !$f(a,b,c,d)=ab+\bar c{(d+\bar a)}$ \\ ! ! ! !\kvnoindex ! ! ! !\kvunitlength=12mm ! ! ! !%généré par la commande scilab : ! ! ! !%tab_karnaugh(’f’,’ab+_c(d+_a)’,vars) ! ! ! !\karnaughmap{4}{$f$}{{$a$}{$c$}{$b$}{$d$}} ! ! ! !{1111~~~~~111~~11} ! ! ! !{%pas de groupements dessinés ! ! ! !} ! |
qui produira le tableau suivant :
f(a,b,c,d) = ab + 
(d + 
)
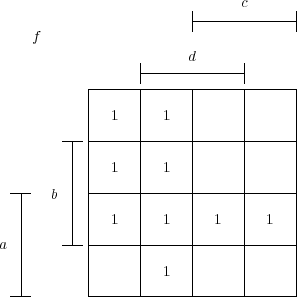
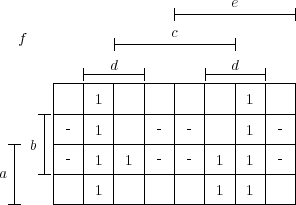
Quelques efforts supplémentaires permettent de tracer des fonction « phi-booléennes » 1 . J’ai alors besoin de deux expressions booléennes : une pour définir la fonction (sur son domaine) une autre pour définir les cases où la fonction n’est pas définie. Il suffit ensuite d’utiliser calcule_tab_karnaugh pour savoir où positionner les 1 dans le tableau de Karnaugh et où placer les caractères signalant que la fonction n’est pas définie ( - pour moi, parfois ∅ est aussi utilisé). Voici un exemple avec une fonction à 5 variables :
-->latex=tab_karnaugh_phi(’f’,’ab+_cd+be_d+acde’,’_db’,vars)
latex = ! ! ! ! !\kvnoindex ! ! ! !\kvunitlength=12mm ! ! ! !%généré par la commande scilab : ! ! ! !%tab_karnaugh_phi(’f’,’ab+_cd+be_d+acde’,’_db’,[ ’e’ ’a’ ’c’ ’b’ ’d’! ! ]) ! ! ! !\karnaughmap{5}{$f$}{{$e$}{$a$}{$c$}{$b$}{$d$}} ! ! ! !{~1-1~~-~~1-1~~-1~1-1~~-~~1-1~1-1} ! ! ! !{%pas de groupements dessinés ! ! ! !} ! |
ce qui donne le tableau :
Le but de cette partie est de générer automatiquement les commandes graphiques pour entourer des groupements dans le tableau de Karnaugh. Comme c’est assez difficile je me suis restreint au cas des fonctions à n variables pour n = 2,3,4,5. la fonction init_variables permet d’initialiser, en fonction de n, un certains nombres de données nécessaires à la gestions des groupements :
-->[num_karnaugh, x_karnaugh, y_karnaugh, vars]=init_variables(3)
vars = !b a c ! y_karnaugh = 2. 2. 2. 2. 1. 1. 1. 1. x_karnaugh = 1. 2. 3. 4. 1. 2. 3. 4. num_karnaugh = 0. 1. 5. 4. 2. 3. 7. 6. |
Si on veut étendre les possibilités des scripts suivants à plus de 5 variables il suffira de
modifier init_variables pour qu’elle initialise correctement les variables
précédentes.
Le problème a été découpé en plusieurs sous-problèmes, associés aux fonctions suivantes :
-->b=convert_base_2(21,5)
b = 1. 0. 1. 0. 1. -->x=convert_base_10(b) x = 21. |
-->L=case_adjacente(0,4)
L = 1. 2. 4. 8. |
-->txt=nom_groupe([0 1 5 4 8 9 13 12],vars)
txt = \bar c |
en 2
parties :
-->L=parties_connexe([0 1 5 4 8 9 13 12],x_karnaugh,y_karnaugh)
L = L(1) 5. 4. 1. 0. L(2) 13. 12. 9. 8. |
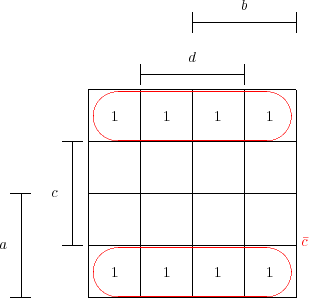
Au final on a une fonction entoure_groupement qui permet d’entourer un
groupement donné par la liste des numéros de cases qui le composent. Par exemple
avec le groupement 
(en 2 morceaux) :
-->txt=nom_groupe([0 1 5 4 8 9 13 12],[’a’ ’b’ ’c’ ’d’])
txt = \bar c -->latex=entoure_groupement([0 1 5 4 8 9 13 12],x_karnaugh,y_karnaugh,’red’,’\bar c’) latex = !\color{red}\put(4.1,1){$\bar c$} ! ! ! !\put(2,3.5){\oval(3.8,0.95)} ! ! ! !\put(2,0.5){\oval(3.8,0.95)} ! |
qui donne bien :
Cette partie est la plus complexe, le but est de récupérer la liste des groupements maximaux automatiquement pour pouvoir ensuite tracer ces divers groupements sur le tableau de Karnaugh. Reconnaître un groupement dans le tableau de Karnaugh d’une fonction booléenne est facile si on connaît la relation d’ordre usuelle sur l’algèbre de bool des fonctions booléennes définie par :
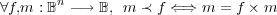
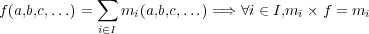
{a,b,c,…} on a x × m ≺ f et 
× m ≺ f alors m ≺ f
donc en partant d’un monôme (canonique) qui apparaît dans le tableau de
Karnaugh, on peut construire des monômes de plus en plus « gros »en regardant pour
chaque variable si en la modifiant en son complémentaire on obtient un nouveau
groupement du tableau. Pour représenter un monôme j’utilise un tableau à n cases
bin tel que :
Par exemple le monôme a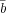
d (à 4 variables) sera représenté par [1 -1 0 1] si l’ordre des
variables est d c b a. En conséquence j’ai découpé le problème en sous-problèmes
associés aux fonctions suivantes :
-->vars
vars = !d b c a ! -->expr_boolean=monome([1 0 1 0], vars) expr_boolean = cd |
-->bin=monome_max(15,’a’,vars)
bin = 0. 0. 0. 1. -->monome(bin, vars) ans = a |
-->G=groupes_max(vars,’a|(~b)’,num_karnaugh)
G = !_b a ! |
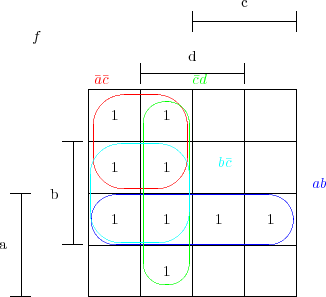
Attention certains groupement maximaux peuvent être absent de cette
liste prendre le cas de la fonction f(a,b,c,d) = ab + 
d + 
on trouve :
f(a,b,c,d) = 
+ ab + 
d
):
-->G=groupes_max(vars,expr_scilab,num_karnaugh)
G = !_a_c ab _cd ! |
alors que le monôme b
est aussi maximal (mais pas obligatoire) :
+ 
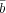cd + bcd tous les monômes sont maximaux mais 
cd et
bcd ne sont pas obligatoire. Un seul d’entre eux est nécessaire à l’écriture d’une
forme réduite de f :
-->forme_reduite(vars,[’ab’ ’_a_b’ ’_acd’ ’bcd’],expr_scilab,num_karnaugh)
ans = !ab _a_b _acd ! |
ce qu’on vérifie facilement sur le tableau de Karnaugh :
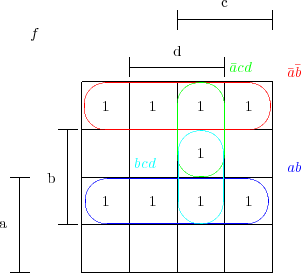
il ne reste plus qu’à intégrer la recherche des monômes maximaux et leur tracé à la fonction qui calcule le tableau de Karnaugh pour obtenir une implémentation complète de la méthode Karnaugh. C’est ce que fait la fonction methode_karnaugh :
-->latex=methode_karnaugh(’f’,’_a(b+cd)+_a_cd’,4)
latex = !$f(a,b,c,d)=\bar a{(b+cd)}+\bar a\bar cd$ \\ ! ! ! !\kvnoindex ! ! ! !\kvunitlength=12mm ! ! ! !%généré par la commande scilab : ! ! ! !%methode_karnaugh(’f’,’_a(b+cd)+_a_cd’,[ ’d’ ’b’ ’c’ ’a’ ]) ! ! ! !\karnaughmap{4}{$f$}{dbca} ! ! ! !{~~~~1~1~1~1~1~1~} ! ! ! !{%les groupements ! ! ! !\color{red}\put(4.1,2.1){$\bar ad$} ! ! ! !\put(0.5,1){\oval(0.95,1.9)} ! ! ! !\put(3.5,1){\oval(0.94,1.88)} ! ! ! !\color{blue}\put(4,4.2){$\bar ab$} ! ! ! !\put(3.5,2){\oval(0.92,3.68)} ! ! ! !}%fin des groupements ! ! ! !\\ ! ! ! !la forme simplifiée est donc :\\ ! ! ! !$f(a,b,c,d)=\bar ad+\bar ab$ \\ ! |
ce qui donne une fois compilé :
f(a,b,c,d) = 
(b + cd) + 
d
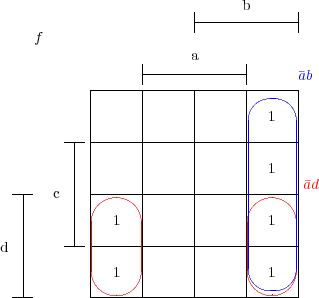
la forme simplifiée est donc :
f(a,b,c,d) = 
d + 
b
L’argument vars permet de spécifier l’ordre des variables, si on veut un ordre différent de l’ordre par défaut (celui renvoyé par init_variables), sinon on donne juste le nombre de variables.
Les fonction sont disponibles dans le Fichier Karnaugh.sce où ont été rajoutés quelques commandes ajoutant un menu à scilab pour tester de manière interactive les fonctions tab_karnaugh, tab_karnaugh_phi et methode_karnaugh. Le code est loin d’être optimal et peut être facilement amélioré par le lecteur intéressé. Il permet cependant de voir comment utiliser scilab pour produire des corrigés d’exercices types en LATEX en laissant scilab s’occuper des calculs mathématiques. On peut ensuite écrire le résultat dans un fichier avec la commande :
mputl(latex,’essai.tex’)
|
et l’insérer dans un fichier LATEXcompilant :
\documentclass{article}
\usepackage{amsmath,color} \input kvmacros \begin{document} \pagestyle{empty} \input essai.tex \end{document} |
