|

|
Centre Emile Borel
|
TRIMESTER ON REAL GEOMETRY
September 12th – December 16th, 2005
Abstracts of the courses
- F. Acquistapace (September 14th -
October 13th, 8 lectures): Around
Hilbert's 17th problem for analytic functions
In this course we will study several properties of the ring of
analytic
functions on a real analytic manifold 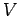 . We will also
study important
properties of the sets which are defined using the ring
. We will also
study important
properties of the sets which are defined using the ring 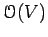 of analytic functions on
of analytic functions on 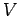 .
.
We will discuss several problems for those global
functions and sets, which are classical for semialgebraic sets and
regular functions, namely:
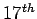 Hilbert Problem: Let
Hilbert Problem: Let 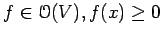 for
any
for
any 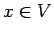 .
Is
.
Is 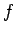 a sum of squares of meromorphic
functions?
a sum of squares of meromorphic
functions? - Nullstellensatz:
Given an ideal
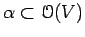 , how can we
caracterize the ideal
, how can we
caracterize the ideal 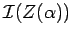 ?
?
- Positivstellensatz:
Given
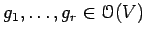 , how
can we caracterize the set
of functions
, how
can we caracterize the set
of functions 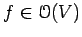 which
are
which
are 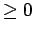 on the set
on the set 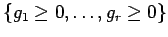 ?
?
- Closure: Is the closure of a global
analytic set still a global
semianalytic set?
- Connected components: Is a union of
connected components of a
global semianalytic set still a global semianalytic set?
- Finiteness: Let
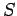 be a global open
(resp. closed) semianalytic set. Can
be a global open
(resp. closed) semianalytic set. Can 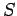 be
described as a finite union of basic open (resp. basic
closed) global semianalytic sets?
be
described as a finite union of basic open (resp. basic
closed) global semianalytic sets?
Here basic open (resp.
basic
closed) sets means
sets of the
form 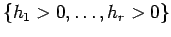 (resp.
(resp.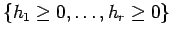 ),
where each
),
where each
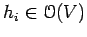 .
.
We point out that almost all these
problems are still open in the
general
case, for dimension 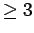 .
.
We will start by showing the relations
between the solution of the 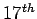 Hilbert problem and the set of orderings
Hilbert problem and the set of orderings 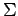 of the
field of fractions or
of
the ring of functions
of the
field of fractions or
of
the ring of functions 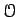 . The crucial point
here is the
so called Artin-Lang Property which relates, roughly
speaking, the sets which are definable by
. The crucial point
here is the
so called Artin-Lang Property which relates, roughly
speaking, the sets which are definable by 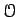 ,
that is, the global semianalytic sets, with the constructible sets
of orderings of
,
that is, the global semianalytic sets, with the constructible sets
of orderings of 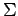 .
.
We will see that this property
holds
always for dimension 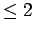 and for a
compact
manifold. As an application, we will show how to solve Hilbert problem
and to prove that the closure and the connected components of a global
semianalytic set in a smooth analytic surface are still global
semianalytic
sets.
and for a
compact
manifold. As an application, we will show how to solve Hilbert problem
and to prove that the closure and the connected components of a global
semianalytic set in a smooth analytic surface are still global
semianalytic
sets.
The Artin-Lang Property is not known for
non compact manifolds of
dimension
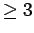 . However, one can solve,
for instance, the finiteness
problem using
more traditional tools, as sheaf theory, Cartan's Theorem B, Whitney's
approximation theorem. For the sake of the audience, we will recall
briefly
these classic technics.
. However, one can solve,
for instance, the finiteness
problem using
more traditional tools, as sheaf theory, Cartan's Theorem B, Whitney's
approximation theorem. For the sake of the audience, we will recall
briefly
these classic technics.
At the end of the course,we will present
some (partial) recent
results
related to the
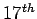 Hilbert Problem, the
Nullstellensatz and the
Positivestellensatz, some of which are still work in progress.
Hilbert Problem, the
Nullstellensatz and the
Positivestellensatz, some of which are still work in progress.
- S. Basu
(November 16th - 25th, 4 lectures): Efficient Algorithms for Computing the
Betti Numbers of Semi-algebraic Sets.
Computing homological information of semi-algebraic
sets (or more generally constructible sets) is an important problem for
several reasons. From the point of view of computational complexity
theory, it is the next logical step after the problem of deciding
emptiness of such sets, which is the signature NP-complete problem in
appropriate models of computation.
In this course I will describe some recent progress in designing
efficient algorithms for computing the Betti numbers of semi-algebraic
sets in several different settings. I will describe a single
exponential time algorithm for computing the first few Betti numbers in
the general case and polynomial time algorithms in case the set is
defined in terms of quadratic inequalities. One common theme underlying
these algorithms is the use of certain spectral sequences -- namely,
the Mayer-Vietoris spectral sequence and the ``cohomological descent''
spectral sequence first
introduced by Deligne.
Certain parts of this work is joint with R. Pollack, M-F. Roy and
(separately) with T. Zell.)
- F. Catanese (November 10th - 29th,
8 lectures) : Deformation
types of real algebraic functions and manifolds
This course will focus on the complex point of view
in the investigation of real algebraic varieties. This means that for
instance the real manifolds are viewed as the real part of a
compact complex manifold, often projective or Kaehler, endowed with an
antiholomorphic involution. And the point of view consists in (instead
of forgetting the non real part) trying to see how the real part embeds
into the complex manifold.
A first example of the advantage of taking this point of view
emerged historically even when dealing with maximal real
polynomials in 1 variable: C. Davis proved with elementary real
analysis that, given (n-1) real critical values, there is a
real polynomial of degree n with these critical values. Later
Thom observed how these kind of results are a consequence of Riemann's
existence theorem, which sheds light more generally on the
classification of real algebraic functions. In fact, once the real
critical value sets are fixed, real algebraic functions are then seen
just as monodromies which are invariant by complex conjugation on the
complex line. I will focus here on the least complicated
examples, such as the counting of Arnold's so-called "snake sequences",
leading to an easy generating function.
Another very easy concept which will be introduced pretty soon is the
concept of the real (orbifold)-fundamental group of a real manifold:
this group contains the complex fundamental group as a subgroup of
index two, and it splits as a semidirect product if there are real
points (observe that from the complex point of view also the empty set
is interesting, as one can easily argue considering the mathematical
charm of the Klein bottle). The use of this concept will be illustrated
by the first important issue, which is the treatment of real structures
on complex tori. Particular enphasis will be set on studying real
elliptic curves and their deformations. This leads to an easy but
important understanding of the genus 1 case of the relation between
moduli spaces of real curves, and the real part of the moduli space of
curves. This relation will then also be treated, even if sketchily, for
the higher genus case. The topic of Nielsen Teichmueller realization,
treated here, will show up and prove quite important also later.
Turning to higher dimensions, and in the Kaehler case, Hodge theory
plays an important role, as was shown by Kharlamov in the 70's, in
order to give topological estimates for Betti numbers of real manifolds.
Another simple application of Hodge theory concerns the existence
of irrational pencils, a theme which in turns leads to surfaces
isogenous to a product and to those among them which are rigid: the
so-called Beauville surfaces. These surfaces are rather important
because they provide interesting examples of complex surfaces which do
not admit real structures, yet can be isomorphic to their complex
conjugate surface. The question of reality or non reality of rigid
surfaces is not yet fully investigated: I will also briefly
discuss the interest of such surfaces concerning the action of
the absolute Galois group, in close relation to Grothendiecks' program
called 'Dessins d' enfants'.
I will then briefly outline the Enriques-Kodaira classification of
complex algebraic surfaces, and the Kodaira classification of
elliptic fibrations. I will then review the status of the
Enriques-Kodaira classification of real algebraic surfaces, through the
contributions of several authors, and with diverse methods. In
particular, I will try to introduce to some important open problems
about real surfaces of special type. One such instance is the
notion of quasi-simplicity considered by Degtyarev, Itenberg and
Kharlamov , which revolves around the problem of comparing deformation
and differentiable equivalence for real structures on complex algebraic
surfaces.
- G. Comte (October 4th - 26th, 8
lectures): Propriétés
métriques en
géométrie modérée
Measures on Grassmannians,
Hausdorff and entropy dimensions,
Vitushkin variations and Lipschitz-Killing curvatures,
Critical locus and entropy,
Semialgebraic complexity of applications,
Quantitative Sard theorems,
Localizations of invariants of integral geometry in tame geometry,
Conormal cone, normal cone and regularity conditions,
Variations of local invariants along regular strata.
- M. Coste (September
13th - 28th, 8
lectures)
: Ensembles constructibles en
géométrie réelle ; géométrie
modérée
I shall give in this course the basics of
semialgebraic
geometry and tame geometry (o-minimal structures) for students who are
not familiar with these topics, in order that they can follow more
specialized courses of the trimester. I shall review the cylindrical
decomposition into cells, stratifications, triangulation, the
local conic structure, Hardt's trivialization theorem, growth
properties of semialgebraic functions. I shall insist on uniformity
results for semialgebraic (or definable) families.
- M. Dickmann (September
13th -
October 24th, 8 lectures) : Théorie
des modèles
en
algèbre et géométrie
Notions et results of model theory necessary for the proof
of
quantifier elimination for real closed fields and related results.
Application of these tools to:
- the structure of semialgebraic sets
and functions,
- the real Nullstellensatz and the
Artin-Lang theorem,
- simple zeros and positivity criteria
for polynomials,
- topology of semialgebraic sets:
cellular decomposition,
dimension, Thom's lemma, triviality of semialgebraic families,
- theory of the real spectrum; real
spectrum of varieties,
- continuous semialgebraic functions
and Nash functions,
Lojasiewicz inequality, Artin's approximation theorem,
- commutative algebra of Nash functions.
- L. van den Dries (November 28th
- December 14th, 8
lectures): Asymptotic differential
algebra
This is differential algebra in a setting where there
is an
ordering and valuation compatible with the derivation, as in Hardy
fields, fields of transseries and H-fields.
- A. Gabrielov (October 20th -
28th, 4 lectures): Pfaffian
functions and sparsity. Real Schubert
Calculus and the B. and M. Shapiro Conjecture
- Lecture 1. Complexity
of computations with Pfaffian functions
Pfaffian functions introduced by Khovanskii in 1970-ies have
polynomial-like global finiteness properties. These functions satisfy a
triangular system of Pfaffian (first order partial differential)
equations with polynomial coefficients. Khovanskii-Bezout theorem gives
an upper bound on the number of real solutions to systems of Pfaffian
equations in terms of the number of Pfaffian equations and the degrees
of polynomials in the definition of Pfaffian functions. Important
special cases of Pfaffian functions are fewnomials, i.e., polynomials
with few nonzero monomials. Complexity of fewnomials as Pfaffian
functions depends on the number of monomials, not on their degrees.
A review of the upper bounds on the complexity of computations with
Pfaffian functions and semi-Pfaffian sets will be given, with the
special attention to fewnomial semialgebraic sets.
- Lecture 2. Betti
numbers of sets defined by formulas with quantifiers
A spectral sequence associated with a surjective mapping allows one to
provide upper bounds for the Betti numbers of a wide class of sets
defined by formulas with quantifiers in terms of the Betti numbers of
auxiliary sets defined by quantifier-free formulas. In the ordinary
semialgebraic case, this approach provides better upper bounds than the
quantifier elimination, especially for the sparse polynomials. It works
also for Pfaffian functions.
- Lecture
3. Rational functions with real critical points,
the Catalan numbers, and the Schubert calculus
How many rational functions of degree 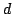 have a
given set of
have a
given set of 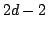 points as their set of
critical points? If we identify
functions that differ by a fractional-linear transformation in the
target space (all such functions have the same critical points) the
answer is
points as their set of
critical points? If we identify
functions that differ by a fractional-linear transformation in the
target space (all such functions have the same critical points) the
answer is 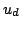 , the Catalan number.
, the Catalan number.
This is equivalent to a problem in the Schubert calculus: How many
codimension 2 affine subspaces in 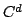 intersect affine lines tangent to the rational normal
curve
intersect affine lines tangent to the rational normal
curve 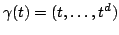 at
at 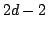 distinct points? The answer
(Schubert, 1886) is
distinct points? The answer
(Schubert, 1886) is 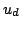 , the Catalan number.
, the Catalan number.
Theorem. Suppose that all 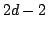 points are real. Then all
points are real. Then all 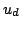 equivalence classes
of rational functions with these
critical points are real (contain real functions).
equivalence classes
of rational functions with these
critical points are real (contain real functions).
The corresponding result in the Schubert calculus is a special case of
the B. and M. Shapiro conjecture.
More general problem: Given 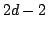 non-overlapping
real segments
non-overlapping
real segments ![$ [a_i,b_i]$](gabrielov/img6.png) , how many rational
functions
, how many rational
functions 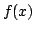 of degree
of degree 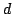 satisfy
satisfy 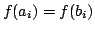 for all
for all 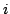 ?
?
The answer is again 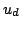 , the Catalan number,
and all these functions (up to
equivalence) are real.
, the Catalan number,
and all these functions (up to
equivalence) are real.
In the Schubert calculus problem, one should replace tangents to the
rational normal curve 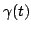 by the
secants through
by the
secants through 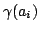 and
and 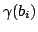 . These secants become tangents when the segments
contract to points.
. These secants become tangents when the segments
contract to points.
If the segments do overlap, not all solutions are real, but there are
lower bounds on the number of real solutions. These results are related
to the B. and M. Shapiro conjecture for flag varieties.
- Lecture 4. Degree of the real Wronski map and
the pole placement problem in control theory.
The Wronski map associates to a 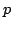 -tuple
of polynomials of degree
-tuple
of polynomials of degree 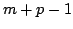 their Wronski
determinant, a polynomial of degree
their Wronski
determinant, a polynomial of degree 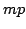 .
If the polynomials are linearly independent, they define a
a point in the Grassmannian
.
If the polynomials are linearly independent, they define a
a point in the Grassmannian 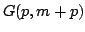 .
Accordingly, the Wronski map can be considered as a map
from
.
Accordingly, the Wronski map can be considered as a map
from 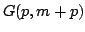 to the projective space
to the projective space 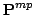 .
The map is finite, and one can define its degree.
In the complex case, this degree equals the number
of standard Young tableaux for the rectangular
.
The map is finite, and one can define its degree.
In the complex case, this degree equals the number
of standard Young tableaux for the rectangular 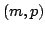 -shape.
In the real case, Young tableax should be counted with the signs
depending on the number of inversions.
Degree of the real Wronski map is zero when
-shape.
In the real case, Young tableax should be counted with the signs
depending on the number of inversions.
Degree of the real Wronski map is zero when 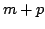 is
even,
and equals the number of standard shifted Young tableaux for an
appropriately defined shifted shape when
is
even,
and equals the number of standard shifted Young tableaux for an
appropriately defined shifted shape when 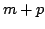 is
odd.
When both
is
odd.
When both 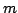 and
and 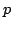 are
even, the Wronski map is not surjective.
These results have important applications to real Schubert
Calculus and to the pole placement problem in control theory.
In particular, non-surjectivity of the real Wronski map
provides examples of linear systems with static output feedback
for which the pole placement problem has no real solutions.
are
even, the Wronski map is not surjective.
These results have important applications to real Schubert
Calculus and to the pole placement problem in control theory.
In particular, non-surjectivity of the real Wronski map
provides examples of linear systems with static output feedback
for which the pole placement problem has no real solutions.
- L. González-Vega (October
20th - 26th, 4 lectures): Using real
algebraic geometry to
improve curve and surface algorithms in computer aided geometric design
applications
By using the surface--to--surface intersection problem in
Computer-Aided Geometric Design as motivation, it will be shown how
techniques from Real Algebraic Geometry can be very helpful in order to
improve in practice the computation of the intersection curve between
two surfaces in 3D space.
The topics covered by the four lectures will be the following:
- Lecture 1: How curves and surfaces are represented and
manipulated in Computer-Aided Geometric Design?
- Lecture 2: Solving intersection problems: dealing with
real algebraic plane curves or surfaces implicitely defined.
- Lecture 3: Computing with offsets: detecting geometric
extraneous components.
- Lecture 4: Interference characterization between
conics and quadrics through Quantifier Elimination.
- S. Kuhlmann (September
26th -
October 17th, 8 lectures) : Polynômes
positifs et
problèmes
de moments
The 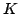 -moment problem originates in
Functional Analysis: for a
linear functional
-moment problem originates in
Functional Analysis: for a
linear functional 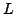 on
on ![$ \mathbb{R}[X_1,\ldots, X_n]$](salma/img3.png) , one
studies the problem of
representing
, one
studies the problem of
representing 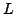 via integration. That is, one asks
whether there exists a
measure
via integration. That is, one asks
whether there exists a
measure 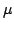 , on Euclidean space
, on Euclidean space 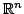 , supported by some given (basic closed
semi-algebraic) subset
, supported by some given (basic closed
semi-algebraic) subset 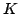 of
of 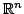 ,
such that for every
,
such that for every ![$ f \in \mathbb{R}[X_1,\ldots, X_n]$](salma/img6.png) we have
we have 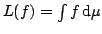 . Via
Haviland's Theorem, the
. Via
Haviland's Theorem, the 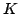 -moment problem is closely
connected to the problem of
representing positive (semi)definite polynomials on
-moment problem is closely
connected to the problem of
representing positive (semi)definite polynomials on 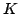 (Hilbert's 17th Problem, Positivstellensatz). In his
solution of the Moment Problem for compact
(Hilbert's 17th Problem, Positivstellensatz). In his
solution of the Moment Problem for compact 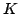 ,
Schmüdgen (1991) exploits this connection, and proves that a
surprisingly strong version of the Positivstellensatz holds in the
compact case. Schmüdgen's result provides a strong motivation to
study
refined versions of the Positivstellensatz. Following rapidly on his
work, several generalizations of his results were worked out. (See F.
Acquistapace's course for related topics in the context of analytic
functions).
The aim of this course is to provide the beginning student with a brief
account of these developments. More precisely, we plan to cover the
following topics:
,
Schmüdgen (1991) exploits this connection, and proves that a
surprisingly strong version of the Positivstellensatz holds in the
compact case. Schmüdgen's result provides a strong motivation to
study
refined versions of the Positivstellensatz. Following rapidly on his
work, several generalizations of his results were worked out. (See F.
Acquistapace's course for related topics in the context of analytic
functions).
The aim of this course is to provide the beginning student with a brief
account of these developments. More precisely, we plan to cover the
following topics:
- Hilbert's 17th Problem,
- Stengle's Positivstellensatz,
- Schmüdgen's Positivstellensatz,
- applications to the multi-dimensional
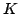 -moment problem,
-moment problem,
- the moment problem for subsets of the
real line,
- extending Schmüdgen's Theorem to
non-compact sets.
If time permits, we will discuss a version of the 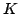 -moment problem, when
-moment problem, when 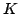 is
assumed to be invariant under the action of a group
is
assumed to be invariant under the action of a group 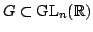 . Throughout the course,
we shall present open problems.
. Throughout the course,
we shall present open problems.
- A. Macintyre (October 17th -
November 15th, 8 lectures): Model
theory of elliptic functions
I will consider model-theoretic questions for the various
structures (T,f), where T is a complex torus of dimension 1
and f is a corresponding
Weierstrass elliptic function. Model-completeness results will be
proved for each individual case, in a formulation where we consider the
f as given by its real and
imaginary parts, which enables us to bring into play various techniques
from o-minimality. The attempt to get a uniform model-completeness is
till under way, and seems to be of great difficulty and considerable
interest. By work of Peterzil and Strachenko, the uniform theory is
known to be o-minimal, because (nontrivially) interpretable in the
theory of the restricted analytics and the global real exponential. I
will discuss the fine detail of this,and lay out the obstructions to
getting uniform model-completeness (these have to do with Manin's work,
and differential equations for the periods).I go on to show how certain
cases (T,f) are even decidable, modulo a
conjecture of Andre on 1-motives and transcendence. I will explain the
connection to the Wilkie-Macintyre proof of decidability for the real
exponential using Schanuel's Conjecture.Finally, I will discuss what is
presently known for related functions, e.g the zeta and sigma functions.
- L. Mahé (November 10th -
December 16th, 12
lectures) : Formes
quadratiques et
géométrie réelle
Real algebraic (and semialgebraic) geometry deals with sets
of real
solutions of polynomial equations (and inequalities), and the algebra
underlying this geometry is the one of sums of squares, or more
generally of quadratic forms. Thus the latter turn out to play a
fundamental role. After some basics of semialgebraic geometry (real
closed fields, semialgebraic sets), real algebra (Nullstellensatz
and Positivstellensatz, real spectrum), and quadratic forms (Pfister
forms, Witt rings), the course will illustrate the interactions between
geometry and quadratic forms with the study of the following three
problems:
- bounding the number of squares
intervening in sums of squares,
- bounding the number of inequalities
needed to describe a
semialgebraic set
- separating connected components of
varieties by signatures of
quadratic forms.
Bibliography:
- J. BOCHNAK, M. COSTE, M.-F. ROY :
Géométrie
algébrique réelle, Springer (1987)
- C. ANDRADAS, L. BRÔCKER, J. RUIZ,
Constructible sets in
real geometry, Springer (1996)
- T.-Y. LAM, The algebraic theory of
quadratic forms, Reading,
Benjamin (1973)
- W. SCHARLAU, Quadratic and hermitian
forms, Springer (1985)
- C. McCrory (September
28th -
October 28th, 16 lectures) : Invariants
and singularities
In the first half of the course I will discuss
Akbulut-King
invariants, which are local topological obstructions for a
semialgebraic set to be homeomorphic to a real algebraic set. I'll
present work with Adam Parusinski defining these invariants using
operators on the ring of constructible functions. as well as related
work by Coste-Kurdyka and Akbulut-King. The second half of the course
will be on virtual Betti numbers, which are global invariants of real
algebraic varieties that Parusinski and I introduced. I'll explain
their relation to the weight filtration of Totaro and to the work of
Bittner and Guillen-Navarro. Throughout the course I will emphasize
open problems.
- G. Mikhalkin
(September 23rd - December 16th, 16 lectures) : Amoebas of algebraic
varieties and tropical geometry
This course is intended to introduce the audience to
a
recent technique in Algebraic Geometry based on application of the
moment map and toric degenerations. One of the simplest examples of the
moment map is the logarithm map that takes a point of the complex torus
C*n to the point in Rn obtained by taking the
logarithm of the
absolute value coordinatewise . The images of holomorphic subvarieties
of C*n under this map are called amoebas.
If one modifies this moment map by taking the logarithm with base t and
lets t to go to infinity then
the amoebas tend to some piecewise-linear
polyhedral complexes in Rn. The dimension of these
limiting complexes
is equal to the dimension of the original varities. It turns out that
such complexes can be considered as algebraic varieties over the
so-called tropical semifield. The term "tropical semifield" appeared in
Computer Science and, in the current context, refers to the real
numbers augmented with the negative infinity and equipped with two
operations, taking the maximum for addition and addition for
multiplication. Polynomials over the tropical semifield are convex
piecewise-linear functions and geometric objects associated to these
polynomials are certain piecewise-linear complexes in Rn.
In the course we consider applications of both the amoebas themselves
and the resulting tropical geometry. One area where amoebas turn out to
be useful is Topology of Real Algebraic Varieties, in particular,
problems related to Hilbert's 16th problem. Using amoebas we show
topological uniqueness of a homologically maximal curve in the real
torus R*2 and
deduce a partial topological description for
hypersurfaces in R*n for n>2. Applications of tropical
geometry
include construction of real algebraic varieties with prescribed
topology (patchworking) as well as enumerative geometry.
A typical problem in enumerative algebraic geometry is to compute the
number of curves of given degree and genus and with a given set of
geometric constraints (e.g. passing through a point or another
algebraic cycle, being tangent to such cycle, etc.). For a proper
number of geometric constraints one expects a finite number of such
curves. Even in the cases when this number is not finite there exists a
way to interpret the answer to such problem as a (perhaps fractional or
negative) Gromov-Witten number. Tropical geometry can be used for
computation of these numbers. In this course we'll compute such numbers
for arbitrary genus and degree when the ambient space is a toric
surface and for genus 0 (and arbitrary degree) if the ambient space is
a higher-dimensional toric variety. In addition we consider real
counterparts of the enumerative problems, in particular, the
Welschinger invariant, and do some computations for them.
- S. Orevkov (September 15th - October 7th, 8
lectures) : Courbes
algébriques réelles, tresses et courbes J-holomorphes
- P. Parrilo (November 21st - 24th, 4
lectures): Computational techniques
based on sum of
squares decompositions
The idea would be to cover the application of convex
optimization
methods to problems in real algebraic geometry. We'd start with the
basic notions of semidefinite programming, and SOS
decompositions. Depending on the audience, we may go into SOS on
quotient or invariants rings, and apply the results to the computation
of Positivstellensatz certificates.
Also, again depending on the audience, we would emphasize different
kind of applications (geometry, dynamical systems, quantum mechanics,
etc.)
- L. Paunescu (December 1st - 16th,
4 lectures), Tree Model,
Relative Newton Polygon and Applications
The Newton Polygon is a powerful tool for analytic
singularities. It
yields the fundamental theorem of Newton-Puiseux. This is an elementary
exposé on this.
For an analytic function germ (convergent power
series) 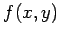 and an analytic arc
and an analytic arc 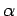 ,
the Newton Polygon of
,
the Newton Polygon of 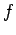 relative to
relative to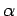 ,
, 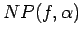 is
defined. A number of important applications
are illustrated.
is
defined. A number of important applications
are illustrated.
Two seemingly unrelated problems are
intimately connected.
The first is the equisingularity problem in 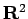 :
For an analytic
family
:
For an analytic
family 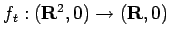 ,
when should it be
called an
equisingular deformation? This amounts to finding a suitable
trivialization condition (as strong as possible) and, of course, a
criterion.
,
when should it be
called an
equisingular deformation? This amounts to finding a suitable
trivialization condition (as strong as possible) and, of course, a
criterion.
The second is on the Morse stability. We define 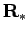 , which is
, which is 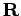 "enriched" with a class of infinitesimals. How to
generalize
the Morse Stability Theorem to polynomials over
"enriched" with a class of infinitesimals. How to
generalize
the Morse Stability Theorem to polynomials over 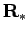 ?
?
The space 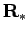 is much
smaller than the space used in
Non-standard Analysis. Our infinitesimals are analytic arcs,
represented by fractional power series, e.g.,
is much
smaller than the space used in
Non-standard Analysis. Our infinitesimals are analytic arcs,
represented by fractional power series, e.g., 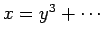 ,
, 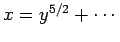 ,
, 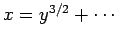 ,
are
infinitesimals at
,
are
infinitesimals at 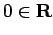 ,
in descending orders.
,
in descending orders.
Thus, 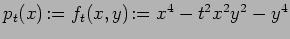 is a family of
polynomials over
is a family of
polynomials over 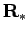 .
This family is not Morse stable:a
triple critical point in
.
This family is not Morse stable:a
triple critical point in 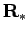 splits
into three when
splits
into three when 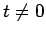 .
.
Bibliography:
- T.-C. Kuo and A. Parusinski, Newton Polygon
Relative to
an Arc, in Real and Complex Singularities (São Carlos,
1998), Chapman & Hall Res. Notes Math., 412, 2000, 76-93.
- T.-C. Kuo and A. Parusinski, Newton-Puiseux Roots
of
Jacobian Determinants, Journal of Algebraic Geometry, 13 (2004),
579-601.
- K. Kurdyka and L. Paunescu, Arc-analytic Roots of
Analytic Functions are Lipschitz, Proceedings of the American
Mathematical Society, 13 (2004), no. 6, 1693-1702.
- T.-C. Kuo and L. Paunescu, Equisingularity in
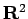 as Morse stability in
infinitesimal calculus,
to appear in the Proceedings of the Japan Academy, June, 2005.
as Morse stability in
infinitesimal calculus,
to appear in the Proceedings of the Japan Academy, June, 2005.
- J.-Ph. Rolin (November 16th - December
15th, 8 lectures) : La
o-minimalité du point de vue de
la géométrie et de l’analyse
This course is the continuation of M. Coste's one. We
will try
to answer, in concrete situations, the question : How to prove that a
given family of sets is o-minimal ?
More precisely, the topics considered will be :
- the properties of global sub-analytic
sets, and a preparation
theorem for sub-analytic functions
- the exp-log-analytic functions
- the behavior of solutions of
differential equations from the
o-minimal point of view
- the relationship with the notion of
quasi-anayticity
- F. Rouillier (September 14th -
28th, 5 lectures),
M.-F. Roy
(October 3rd - 12th, 5 lectures), S.
Basu (November 14th - November 28th, 5 lectures) : Algorithms in
real algebraic geometry
- F. Rouillier:
- Univariate solving.
- Properties and applications of Gröbner bases
(localization and
elimination).
- Zero-dimensional solving (Hermite quadratic forms,
RUR)
- Well-behaved parametric systems
- Some applications of polynomial system solving
- M-F. Roy:
- Discriminants, Resultants, Subresultants
- Complexity of cylindrical decomposition
- Applications of cylindrical decomposition
- Complexity of finding a point in every connected
components of an
algebraic set
- Complexity of finding non empty sign conditions on
a
family of
polynomials
- S. Basu:
- General Decision Problem and Quantifier
Elimination.
- Uniform (Local) Quantifier
Elimination and its application in constraint databases.
- Computing Roadmaps for Algebraic Sets.
- Computing Roadmaps in general and computing
descriptions of
connected components.
- Computing coverings by contractible sets and
applications.
- E. Shustin (September 29th -
October 14th, 4 lectures):
Patchworking construction and its applications
- Construction of real non-singular algebraic varieties:
Viro's method and its
modifications.
- Patchworking
construction in singularity theory and algebra over the complex and real field.
- Patchworking
construction in the tropical geometry.
- F. Sottile
(November 14th - 29th, 8 lectures) : Real
solutions to
equations from geometry
Understanding, finding, or even deciding the existence of
real solutions to a system of equations is a very difficult problem
with many applications. While it is hopeless to expect much in general,
we know a surprising amount about these questions for systems which
possess additional structure. Particularly fruitful---both for
information on real solutions and for applicability---are systems whose
additional structure comes from geometry. Such equations from geometry
for which we have information about their real solutions will be the
subject of this short course.
We will focus on equations from toric varieties and homogeneous spaces,
particularly Grassmannians. Not only is much known in these cases, but
they encompass some of the most common applications. The results we
discuss may be grouped into three themes:
(1) Upper bounds on the number of real solutions.
(2) Geometric problems that can have all solutions be real.
(3) Lower bounds on the number of real solutions
Upper bounds as in (1) bound the complexity of the set of real
solutions---they are one of the sources for the theory of o-minimal
structures which are an important topic in this trimester. Lower bounds
as in (3) give an existence proof for real solutions. Their most
spectacular manifestation is the non-triviality of the Welschinger
invariant, which was computed via tropical geometry. This is also
explained in other courses this trimester at the Centre Borel.
The course will have three parts, grouped by geometry:
I) Overview (Lecture 1)
II) Toric Varieties (Lectures 2--4)
III) Grassmannians (Lectures 5--8)
Topics for each lecture
- Overview. Upper and lower bounds, Shapiro conjecture,
and rational curves interpolating points in the plane.
- Sparse polynomial systems and toric varieties.
Kouchnirenko's Theorem and Groebner degeneration.
- Upper bounds. Descartes' rule of signs, Khovanski's
fewnomial bound, bound for circuits.
- Lower bounds. Soprunova-Sottile toric lower bound.
- Grassmannians. Wronski map, problem of 4 lines.
Reality in the Schubert calculus via Schubert induction, Vakil's
Theorem.
- The Shapiro conjecture for Grassmannians.
Computational and theoretical evidence. Sums of squares and
discriminants.
- Eremenko and Gabrielov's elementary proof of Shapiro
Conjecture for 2-planes. Maximally inflected curves.
- Lower bounds for the Wronski map via sagbi
degeneration.
There will be typeset notes available for each lecture.
- B.
Teissier (September
19th - October 17th, 5 lectures) : Introduction
to valuations in
algebraic geometry
Je donnerai les bases de la theorie des valuations en
insistant sur leur role en geometrie algébrique. J'essaierai de
rappeler et d'illustrer les notions de géométrie
algébrique utilisées pour les rendre accessibles aux
non-experts.
I will explain the basics of the theory of valuations, insisting on
their role in algebraic geometry. I shall try to recall and illustrate
the notions of algebraic geometry which are used, in order to make them
accessible to non-experts.
D. Gondard
(October 24th -
November 14th, 3 lectures) : Valuations
in real algebra
Le cours, qui sera effectué dans le cadre des
corps ordonnables, débutera avec la compatibilité
d'un préordre et d'une valuation, et les cas particuliers
des éventails et éventails valués. Ensuite nous
présenterons la théorie des ordres de niveau
supérieur, et ses liens avec les sommes de puissances ; puis il
sera etudié la notion de clôture algébrique d'un
corps muni d'un éventail valué. Enfin nous donnerons
quelques applications des ces notions en géométrie
algébrique réelle et montrerons le lien avec les R-places
et l'anneau d'holomorphie réel.
We shall work in the framework of real fields, start with the
compatibility of a preordering with a valuation, and then turn to the
special case of fans and valuation fans. Afterwards we shall present
the higher level orderings, and their links with sums of powers, and
study the notion of algebraic closure under algebraic extensions of a
fields equipped with a valuation fan. Last we shall give some
applications to Real Algebraic Geometry and show the links with
R-places and with the real holomorphy ring.

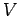 . We will also
study important
properties of the sets which are defined using the ring
. We will also
study important
properties of the sets which are defined using the ring 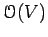 of analytic functions on
of analytic functions on ![]() and for a
compact
manifold. As an application, we will show how to solve Hilbert problem
and to prove that the closure and the connected components of a global
semianalytic set in a smooth analytic surface are still global
semianalytic
sets.
and for a
compact
manifold. As an application, we will show how to solve Hilbert problem
and to prove that the closure and the connected components of a global
semianalytic set in a smooth analytic surface are still global
semianalytic
sets.![]() . However, one can solve,
for instance, the finiteness
problem using
more traditional tools, as sheaf theory, Cartan's Theorem B, Whitney's
approximation theorem. For the sake of the audience, we will recall
briefly
these classic technics.
. However, one can solve,
for instance, the finiteness
problem using
more traditional tools, as sheaf theory, Cartan's Theorem B, Whitney's
approximation theorem. For the sake of the audience, we will recall
briefly
these classic technics.![]() Hilbert Problem, the
Nullstellensatz and the
Positivestellensatz, some of which are still work in progress.
Hilbert Problem, the
Nullstellensatz and the
Positivestellensatz, some of which are still work in progress.
![$ \mathbb{R}[X_1,\ldots, X_n]$](salma/img3.png) , one
studies the problem of
representing
, one
studies the problem of
representing 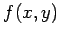 and an analytic arc
and an analytic arc 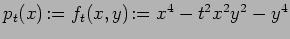 is a family of
polynomials over
is a family of
polynomials over 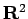 as Morse stability in
infinitesimal calculus,
to appear in the Proceedings of the Japan Academy, June, 2005.
as Morse stability in
infinitesimal calculus,
to appear in the Proceedings of the Japan Academy, June, 2005.