BO no25 du 30 juin 2005
Page officielle
Version imprimable (pdf)
Concours externe et interne du CAPLP2 - programme permanent
Section mathématiques - sciences physiques
Programme de mathématiques
Le programme des épreuves écrites des concours externe et interne d'accès au deuxième grade
du corps des professeurs de lycée professionnel est défini par les titres A et B
ci-dessous.
Le programme des épreuves orales des concours externe et interne porte sur le titre A augmenté des paragraphes suivants du
titre B.
I. Analyse: §2. Fonctions d'une variable réelle; §3. Équations différentielles.
II. Algèbre: §1. Nombres complexes.
III. Combinatoire. Statistiques. Probabilités : §1. Combinatoire - §2. Statistique descriptive - §2. Probabilités.
IV.
Géométrie: §1. Géométrie du plan et de l'espace.
Annexe
A- Programme des lycées professionnels
Ce programme comporte tous les
programmes des classes de lycées professionnels en vigueur l'année du concours.
B- Programme complémentaire
I. ANALYSE
Notions élémentaires sur les suites et les
séries.
a) Propriétés fondamentales du corps R des réels:
majorants, minorants, borne
supérieure, borne inférieure. Toute partie non vide de R majorée admet une borne
supérieure (admis). Aucune construction de R n'est au programme.
b) Convergence d'une suite de nombres réels; opérations sur les suites convergentes. Convergence
d'une suite monotone; exemples de suites adjacentes.
Exemples d'études de suites définies par une relation de
récurrence Un+1=f(Un).
c) Définition de la convergence d'une série à termes réels. Convergence des séries
géométriques.
Séries à termes positifs : comparaison des deux séries dans
le cas où Un ≤ Vn et dans le
cas où Un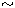 Vn. Comparaison à une
intégrale; convergence des séries de Riemann.
Comparaison à une série géométrique, règle de D'Alembert. Comparaison à
une série de
Riemann.
Vn. Comparaison à une
intégrale; convergence des séries de Riemann.
Comparaison à une série géométrique, règle de D'Alembert. Comparaison à
une série de
Riemann.
Séries absolument convergentes. Convergence d'une série alternée dont la valeur absolue du
terme général décroît et tend vers 0.
Fonctions d'une variable réelle
Les fonctions considérées dans ce chapitre sont définies sur un intervalle de
R non réduit
à un point.
a)
Fonctions à valeurs réelles: continuité,
dérivation
1) Limite et continuité en un point. Opérations sur les limites. Limites d'une fonction monotone.
Propriété fondamentale des fonctions continues (admise): l'image d'un intervalle
(respectivement d'un segment) est un intervalle (respectivement un
segment).
Continuité de
la fonction réciproque d'une fonction strictement monotone et continue
sur un intervalle.
2) Dérivée en un point: dérivabilité sur un intervalle.
Fonction dérivée. Opérations sur les
fonctions dérivées. Dérivée de la composée de deux fonctions,
d'une fonction réciproque.
Définition des fonctions de classe Cp, C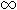 . Dérivée n-ième d'un
produit (formule de Leibniz).
. Dérivée n-ième d'un
produit (formule de Leibniz).
3) Théorème de Rolle, formule des accroissements finis, inégalités des accroissements finis.
Caractérisation des fonctions constantes, monotones et strictement
monotones.
4) Etude locale des fonctions. Comparaison des fonctions au voisinage d'un point : fonction
négligeable devant une autre, fonctions équivalentes (notation
f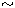 g). Comparaison des
fonctions exponentielle, puissance et logarithme au voisinage de
g). Comparaison des
fonctions exponentielle, puissance et logarithme au voisinage de
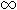 .
.
Développements limités, opérations sur les développements limités. Formule de Taylor-Young.
Développements limités des fonctions usuelles.
5) Fonctions usuelles: fonctions circulaires, circulaires réciproques, logarithmes,
exponentielles, puissances, hyperboliques, hyperboliques
réciproques.
b) Fonctions à valeurs réelles : intégration sur un
segment
Les seules connaissances exigibles portent sur l'intégration des fonctions continues par
morceaux.
1) Linéarité de l'intégrale.
Si a ≤ b, 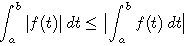 .
.
Additivité par rapport à l'intervalle d'intégration. Somme de Riemann d'une fonction
continue; convergence de ces sommes.
2) Primitives d'une fonction continue sur un intervalle
Théorème fondamental du calcul différentiel et intégral: si f est une fonction continue sur
un intervalle I et a un point de I, la fonction
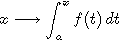 est l'unique primitive de f sur I
s'annulant en a; inversement pour tout primitive F de f sur I et pour tout couple
(a,b) de points de I,
est l'unique primitive de f sur I
s'annulant en a; inversement pour tout primitive F de f sur I et pour tout couple
(a,b) de points de I,
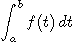 =F(b)-F(a).
=F(b)-F(a).
Intégration par parties, changement de variable. Exemples de calcul de primitives notamment
de fonctions rationnelles, de polynômes trigonométriques.
Formule de Taylor avec reste intégral.
3) Exemples de calcul de valeurs approchées d'une intégrale. Exemples de calculs d'aires
planes, de volumes, de masses.
c) Fonctions à valeurs dans C
Extension à ces fonctions des notions et propriétés
suivantes :
Dérivée en un point. Opérations sur les dérivées. Développements limités, formule de
Taylor-Young.
Fonction t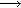 eit (t réel). Symbole ez (z complexe), règles de calcul.
eit (t réel). Symbole ez (z complexe), règles de calcul.
Dérivation et intégration de t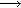 eat (t
réel, a complexe).
eat (t
réel, a complexe).
Intégration, intégration par parties, formule de Taylor avec
reste intégral.
d) Notions sur les intégrales impropres
Définition de la convergence des intégrales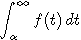 ;
extension aux intégrales
;
extension aux intégrales
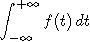 .
Convergence des intégrales de Riemann:
.
Convergence des intégrales de Riemann:
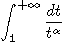 et
et
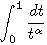 où
où 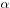 est
réel.
est
réel.
Intégrales de fonctions positives: comparaison dans les cas f ≤ g
et f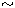 g.
g.
Intégrales absolument convergentes.
Equations différentielles
a) Définition sur un intervalle d'une solution d'une équation différentielle de la
forme y'=f(x,y); courbe intégrale (aucun théorème d'existence
n'est au programme).
b) Equation différentielle linéaire du premier ordre ay'+by=c où a,b,c sont des fonctions
numériques continues sur un même intervalle. Recherche, sur un intervalle où a ne s'annule
pas, de la solution satisfaisant à une condition initiale
donnée.
c) Equation différentielle linéaire du second ordre à coefficients constants, dont le second
membre est de la forme emtP(t), P étant un polynôme et
m un réel ou un complexe.
Notions sur les séries de Fourier
a) Coefficients et série de Fourier d'une fonction 2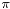 -périodique continue par
morceaux à valeurs complexes (expression
sous forme exponentielle, expression en cosinus et sinus).
-périodique continue par
morceaux à valeurs complexes (expression
sous forme exponentielle, expression en cosinus et sinus).
b) Théorème de Dirichlet (admis): convergence de
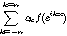 vers la demi-somme des limites à droite et à
gauche de f au point x
lorsque
f est de classe C1 par morceaux. Formule de Parceval (admise): expression de l'intégrale du carré du
module sur une période à l'aide des coefficients de Fourier lorsque f est continue par morceaux.
vers la demi-somme des limites à droite et à
gauche de f au point x
lorsque
f est de classe C1 par morceaux. Formule de Parceval (admise): expression de l'intégrale du carré du
module sur une période à l'aide des coefficients de Fourier lorsque f est continue par morceaux.
Exemples de
développement en série de Fourier de fonctions d'une variable
réelle.
Notions sur les fonctions de plusieurs variables réelles
Définition d'une application d'une partie de Rp dans Rn (se limiter à n ≤3, p ≤ 3).
Continuité en un point.
Dérivées partielles d'ordre un et supérieur à un.
Théorème de Schwarz (admis).
II. ALGEBRE
1) Nombres complexes
a) Corps des nombres complexes; module d'un nombre complexe. Argument d'un nombre complexe non nul; notation
ei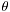
b) Formule de Moivre. Formules d'Euler. Résolution de l'équation
zn=a. Applications trigonométriques de nombres
complexes. Lignes de niveau des fonctions z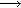
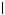 z-a
z-a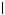 et
z
et
z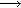 Arg(z-a).
Arg(z-a).
c) Transformations géométriques définies par z'=az+b,
z'=z et z'=1/z
2) Polynômes et fractions rationnelles
a) Algèbre K[X] des polynômes à coefficients dans
K (K est
R ou C).
Degré, division suivant les puissances décroissantes.
Racines, ordre de multiplicité d'une racine. Polynômes irréductibles sur
C ou R. Factorisation. (La
construction de l'algèbre des polynômes formels n'est pas au programme, les candidats n'auront pas à connaitre la
notion de PGCD).
Fonctions rationnelles: pôles, zéros, ordre de multiplicité d'un pôle ou
d'un zéro.
Décomposition en éléments simples dans R(X) et
dans C(X) (admis).
3) Algèbre linéaire
a) Espace vectoriel sur le corps K
(K=R
ou C)
1) Espaces vectoriels, applications linéaires, formes
linéaires.
Exemples fondamentaux: espaces des vecteurs du plan et de l'espace, espace
Kn.
Composition des applications linéaires, isomorphismes, endomorphismes,
automorphismes. Groupe linéaire GL(E).
2) Combinaisons linéaires, sous-espace vectoriel, sous-espace vectoriel
engendré par p vecteurs. Image et noyau d'une
application linéaire. Espace vectoriel 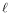 (E,F).
(E,F).
3) Espaces vectoriels de dimension finie
Dans un espace admettant une famille génératrice finie, définition des familles libres,
des familles génératrices et
des bases. Exemple fondamental: base canonique de 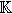 n.
Dimension. Rang
d'une famille de p vecteurs.
n.
Dimension. Rang
d'une famille de p vecteurs.
Sous-espaces vectoriels supplémentaires, projecteurs.
c) Matrices
Espace vectoriel Mp,q(K) des matrices à p lignes et q
colonnes.
Isomorphisme entre 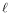 (
Kq,Kp) et
Mp,q(K).
(
Kq,Kp) et
Mp,q(K).
Produit matriciel, transposition. Algèbre Mn(Kn);
matrices inversibles;
groupe linéaire GLn(Kn).
Changement de base pour une application linéaire, matrice de passage.
d) Eléments propres.
Valeurs propres, vecteurs propres pour une
application linéaire.
Diagonalisation en dimension 2 ou 3.
e) Déterminant d'une matrice.
Calcul du déterminant d'une matrice en dimension 2 et en dimension 3.
f) Systèmes d'équations linéaires.
Pratique de la méthode de Gauss pour la résolution de systèmes d'équations.
III. COMBINATOIRE - STATISTIQUES - PROBABILITÉS
1) Combinatoire
a) Nombre des applications d'un ensemble à p éléments dans un ensemble à n éléments; nombre des injections;
arrangements. Nombre des permutations d'un ensemble à n
éléments.
b) Nombre des parties à p éléments d'un ensemble à
n éléments, combinaison.
c) Formule du binôme.
2) Statistique descriptive
a) Analyse statistique d'une variable observée sur les individus d'une population. Exemples de variables qualitatives et
de variables quantitatives: effectifs, fréquences, histogrammes.
Caractéristiques de position (moyenne, médiane, mode, quantile).
Caractéristiques de dispersion (variance, écart-type).
b) Analyse statistique élémentaire de deux variables observées sur les individus d'une population.
Tableaux d'effectifs,
fréquences marginales, fréquences conditionnelles.
Covariance et coefficient de corrélation linéaire. Ajustement affine par la
méthode des moindres carrés.
Droites de régression.
3) Probabilités
a) Probabilité sur les ensembles finis: vocabulaire des
événements, probabilité,
équiprobabilité.
Exemples simples de dénombrement.
Probabilités conditionnelles, événements
indépendants.
b) Variables aléatoires
1) Définition d'une variable aléatoire à valeurs réelles. Evénements liés
à une variable aléatoire.
2) Variables aléatoires discrètes:
Loi de probabilité. Fonction de répartition: F(x)=P(X ≤
x).
Moments: espérance, variance, écart-type.
lois discrètes usuelles: loi uniforme, de Bernoulli, binômiale,
de Poisson.
3) Vecteurs aléatoires à valeurs dans R2 discrets.
Loi de probabilité d'un vecteur à valeurs dans R2. Lois
marginales.
Indépendance de deux variables aléatoires réelles.
Linéarité de l'espérance mathématique. Espérance mathématique du
produit de deux variables aléatoires indépendantes.
Variance d'une somme de variables aléatoires, covariance.
4) Variables aléatoires à densité.
On dira qu'une variable aléatoire X à valeurs réelles admet une densité f
si, quel que soit l'intervalle [a,b]
de R, P(a ≤ X ≤ b)=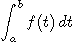 où f est une fonction à valeurs réelles positives ayant
un nombre fini de points de discontinuité et telle que
où f est une fonction à valeurs réelles positives ayant
un nombre fini de points de discontinuité et telle que
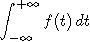 =1.
=1.
Moments: espérance, variance, écart-type.
Lois définies par une densité usuelle: loi uniforme, exponentielle,
normale.
IV. GEOMETRIE
1) Géométrie du plan et de l'espace
a) Calcul vectoriel
Produit scalaire, lien avec la norme et la distance.
Expression dans une base orthonormale.
Relations métriques dans le triangle. Orthogonalité.
Produit vectoriel dans l'espace orienté.
Systèmes de coordonnées (cartésiennes, polaires, cylindriques, sphériques); changement de repère orthonormal.
Barycentre.
b) Configurations
Droites et plans: direction, parallélisme, intersection, orthogonalité. angle de deux droites, de deux plans, d'une
droite et d'un plan. Distance d'un point à une droite (à un plan). Equations cartésiennes et représentations
paramétriques des droites et plans. Equation normale.
Cercles dans le plan: équation cartésienne.
Sphères: équations cartésiennes. Intersection sphère et plan.
Coniques: équation réduite et équation paramétrique d'une conique en
repère orthonormal.
c) Applications affines
Projections, affinités orthogonales; conservation des barycentres par une application affine.
Isométries du plan; réflexions, rotations, déplacements.
Exemples d'isométries de l'espace; réflexions, rotations, vissages.
2)
Géométrie différentielle des courbes planes
a) Fonction d'une variable réelle à valeurs dans R2: limite, continuité, dérivée en un point; opérations sur les
dérivées. Dérivée d'un produit scalaire, d'un produit
vectoriel.
Fonction de classe Cp. Définition des développements
limités.
b) Etude locale: point régulier; tangente. Etude de la position locale d'une courbe par rapport à une droite; branches
infinies.
Exemples de construction de courbes paramétrées.
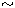 Vn. Comparaison à une
intégrale; convergence des séries de Riemann.
Comparaison à une série géométrique, règle de D'Alembert. Comparaison à
une série de
Riemann.
Vn. Comparaison à une
intégrale; convergence des séries de Riemann.
Comparaison à une série géométrique, règle de D'Alembert. Comparaison à
une série de
Riemann. . Dérivée n-ième d'un
produit (formule de Leibniz).
. Dérivée n-ième d'un
produit (formule de Leibniz).
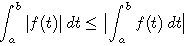 .
.
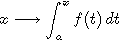 est l'unique primitive de f sur I
s'annulant en a; inversement pour tout primitive F de f sur I et pour tout couple
(a,b) de points de I,
est l'unique primitive de f sur I
s'annulant en a; inversement pour tout primitive F de f sur I et pour tout couple
(a,b) de points de I,
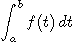 =F(b)-F(a).
=F(b)-F(a).
 eit (t réel). Symbole ez (z complexe), règles de calcul.
eit (t réel). Symbole ez (z complexe), règles de calcul.
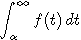 ;
extension aux intégrales
;
extension aux intégrales
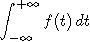 .
Convergence des intégrales de Riemann:
.
Convergence des intégrales de Riemann:
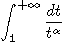 et
et
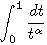 où
où 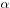 est
réel.
est
réel.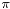 -périodique continue par
morceaux à valeurs complexes (expression
sous forme exponentielle, expression en cosinus et sinus).
-périodique continue par
morceaux à valeurs complexes (expression
sous forme exponentielle, expression en cosinus et sinus).
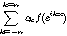 vers la demi-somme des limites à droite et à
gauche de f au point x
lorsque
f est de classe C1 par morceaux. Formule de Parceval (admise): expression de l'intégrale du carré du
module sur une période à l'aide des coefficients de Fourier lorsque f est continue par morceaux.
vers la demi-somme des limites à droite et à
gauche de f au point x
lorsque
f est de classe C1 par morceaux. Formule de Parceval (admise): expression de l'intégrale du carré du
module sur une période à l'aide des coefficients de Fourier lorsque f est continue par morceaux.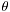
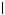 z-a
z-a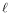 (E,F).
(E,F).
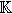 n.
Dimension. Rang
d'une famille de p vecteurs.
n.
Dimension. Rang
d'une famille de p vecteurs.