DÉFINITIONS ET THÉORÈMES EN ALGÈBRE BILINÉAIRE (pdf)
Adjoint d'un endomorphisme
L'adjoint d'un endomorphisme u d'un espace vectoriel euclidien (respectivement hermitien) (E,φ) est l'unique endomorphisme u* vérifiant :
∀ (x,y) ∈ E2, φ(u(x),y)=φ(x,u*(y)).
Dans une base orthonormée, la matrice de u* est la transposée (respectivement l'adjointe) de celle de u.
Adjointe d'une matrice
L'adjointe d'une matrice est la transposée de sa conjuguée. On la note A* et on a donc A*=tĀ
Antisymétrique
Un endomorphisme u d'un espace euclidien (E,φ) est dit antisymétrique s'il est égal à l'opposé de son adjoint (u*=-u), c'est-à-dire si u vérifie
∀ (x,y) ∈ E2, φ(u(x),y)=-φ(x,u(y)).
Un endomorphisme est antisymétrique si et seulement si sa matrice dans une base orthonormée est antisymétrique.
Soit E un espace vectoriel sur un corps K.
Une forme bilinéaire φ sur E est une application de E2 dans K linéaire à gauche et à droite, c'est-à-dire que
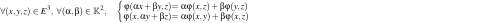
Une forme bilinéaire est dégénérée si la matrice qui la représente dans une base donnée n'est pas inversible. Elle est dite non dégénérée sinon.
Si q est une forme quadratique définie, alors sa forme polaire est non dégénérée. La réciproque est fausse.
Une forme bilinéaire ou sesquilinéaire φ sur un espace vectoriel E est dite définie lorsque, pour tout x∈E, φ(x,x)=0 ⇒ x=0 ; autrement dit s'il n'existe pas de vecteur isotrope non nul.
- - Une forme quadratique q sur un espace vectoriel E est dite définie lorsque, pour tout x∈E, q(x)=0 ⇒ x=0 ; autrement dit lorsque sa forme polaire est définie.
- -Une matrice A de Mn(ℝ) est dite définie si, pour tout X, tXAX=0⇒X=0; autrement dit si c'est la matrice d'une forme quadratique définie positive. Une matrice définie est inversible mais la réciproque est fausse.
Un espace euclidien est un espace vectoriel réel de dimension finie muni d'un produit scalaire φ.
La norme associée est appelée norme euclidienne.
∀ (x,y) ∈ E2, &psi(x,y)=ψ(t,x).
- -Un produit hermitien sur un ℂ-espace vectoriel E est une forme sesquilinéaire hermitienne qui est de plus définie positive.
- -Un espace hermitien est un ℂ-espace vectoriel E de dimension finie muni d'un produit hermitien.
- -Un endomorphisme u d'un espace hermitien est dit hermitien lorsqu'il est égal à son adjoint. Un endomorphisme est hermitien si sa matrice dans une base orthonormée est hermitien.
Une matrice hermitienne est une matrice dont la transposée est égale à la conjuguée : tA =Ā
Isométrie
- -Une isométrie d'un ensemble E muni d'une distance d est une application f de E dans E qui vérifie
∀ (x,y)∈ E2, d(f(x),f(y))=d(x,y).
- -Une isométrie vectorielle d'un espace euclidien E est une application f de E dans E qui conserve le produit scalaire :
∀ (x,y)∈ E2, φ(f(x),f(y))=φ(x,y).
f est une isométrie vectorielle si et seulement si elle est linéaire et elle conserve la norme. Les isométries vectorielles coïncident avec les automorphismes orthogonaux pour φ.
Un vecteur est dit isotrope pour une forme bilinéaire ou sesquilinéaire lorsqu'il est orthogonal à lui-même.
Matrice d'une forme bilinéaire
La matrice d'une forme bilinéaire φ sur un espace vectoriel E de dimension finie dans une base (e1,...,en) est la matrice A de coefficients aij=&phi(ei,ej). On a φ(x,y)=tXAY.
Matrice d'une forme quadratique
Normal
Un endomorphisme normal d'un espace euclidien ou hermitien est un endomorphisme qui commute avec son adjoint.
Soit E un espace muni d'une forme bilinéaire symétrique ou d'une forme sesquilinéaire hermitienne φ.
- -Deux vecteurs x et y de E sont orthogonaux si φ(x,y)=0.
- -L'orthogonal d'un élément x de E est l'ensemble des vecteurs de E orthogonaux à x. C'est un sosu-espace vectoriel de E.
- -Un endomorphisme u d'un espace euclidien E est dit orthogonal lorsque
∀ (x,y)∈ E2, φ(u(x),u(y))=φ(x,y).
- -Le groupe orthogonal, noté O(E), de E est l'ensemble des endomorphismes orthogonaux.
- -Une matrice A est dite orthogonale lorsque tAA=In. C'est une matrice de passage d'une base orthonormée à une autre.
- -Deux matrices A et B sont orthogonalement semblables si ce sont les matrices d'un même endomorphisme dans deux bases orthonormées.
La forme polaire d'une forme quadratique q est l'unique forme bilinéaire symétrique φ telle que, pour tout x∈ E, q(x)=φ(x,x). Elle est définie par
φ(x,y)=⅟2 (q(x+y)-q(x)-q(y))=⅟4 (q(x+y)-q(x-y))
.
Une forme bilinéaire symétrique ou une forme sesquilinéaire hermitienne φ est dite positive lorsque, pour tout x ∈ E, φ(x,x) ≥ 0.
Une matrice symétrique A de Mn(ℝ) est dite positive si c'est la matrice d'une forme bilinéaire positive.
Préhilbertien
Un espace préhilbertien complexe est un espace muni d'un produit hermitien.
Une forme quadratique sur un ℝ-espace vectoriel E est une application q de E dans ℝ telle qu'il existe une forme bilinéaire symétrique φ sur ℝ vérifiant, pour tout x dans E, q(x)=φ(x,x).
Si x a pour coordonnées (x1,...x2) dans une base de E, alors
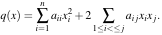
Semi-linéaire
Une application d'un ℂ-espace vectoriel E vers un ℂ-espace vectoriel F est semi-linéaire si, pour tout (x,y) ∈ E2 et pour tout λ ∈ ℂ, on a f(x+y)=f(x)+f(y) et f(λx)=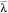 f(x).
f(x).
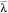 f(x).
f(x).Soit E un ℂ-espace vectoriel. Une forme sesquilinéaire sur E est une application de E2 dans ℂ semi-linéaire à gauche et linéaire à droite.
Spécial
Le groupe spécial orthogonal, noté SO(E), est le sous-groupe du groupe orthogonal formé des endomorphismes orthogonaux de déterminant égal à +1.
- -Une forme bilinéaire φ est symétrique si, pour tout (x,y) ∈ E2, φ(x,y)=φ(y,x). En dimension finie, il es équivalent de dire que sa matrice dans une base quelconque est symétrique.
- -Un endomorphisme d'un espace euclidien est dit symétrique ou autoadjoint s'il est égal à son adjoint.
- -Un endomorphisme u d'un espace hermitien E est dit unitaire lorsque
∀ (x,y) ∈ E2, φ(u(x),u(y))=φ(x,y)
- -Le groupe unitaire, noté U(E), de E est l'ensemble des endomorphismes unitaires.
- -Une matrice A de Mn(ℂ) est dite unitaire lorsque t AA=In. C'est une matrice de passage d'une base orthonormée à une autre.
- -Deux matrices A et B sont unitairement semblables si ce sont les matrices d'un même endomorphisme dans deux bases orthonormées.